| Почему область решений была взята как многоугольник ОАВС. А как же точки (567;0) и (0;320). На мой взгляд, я бы выбрал многоугольник с точками О (567;0) (0;320). Ведь они являются областью пересечения двух ограничений |
Решение транспортных задач
Целью лекции является ознакомление учащихся с методикой оптимизации математических моделей транспортных задач. На конкретных примерах разобраны типичные случаи использования программы "Поиск решения".
Задача 3.1
Определить план доставки грузов от поставщиков потребителям при условии минимальной стоимости всех перевозок. Данные приведены в таблице.
| Тарифы на перевозку | Ресурсы поставщиков | |||||
|---|---|---|---|---|---|---|
| Потребители | 1 | 2 | 3 | 4 | 5 | |
| Поставщик 1 | 20 | 30 | 50 | 40 | 10 | 310 |
| Поставщик 2 | 30 | 20 | 40 | 10 | 50 | 260 |
| Поставщик 3 | 40 | 30 | 20 | 60 | 20 | 280 |
| Потребность потребителей | 180 | 80 | 200 | 160 | 220 | 850/840 |
В выделенной области таблицы указаны тарифы (транспортные расходы) на перевозку от данного поставщика к каждому потребителю. Транспортные расходы здесь являются условным понятием. В различных задачах в роли их могут выступать также расстояние, время и т.п. В последнем столбце указаны ресурсы поставщиков. Если перевозки осуществляются однотипным транспортом, то это может быть просто число перевозок. Иначе это может быть объем груза, штуки или тонны. В нижней строке указаны потребности потребителей.
В транспортных задачах с закрытой моделью запасы поставщиков совпадают с потребностями потребителей. В данной постановке задачи отражена ситуация, когда предложение (850 перевозок) превышает спрос (840 перевозок). Часто в таких случаях ограничения для пунктов отправления записывают в виде неравенств, а ограничения для пунктов назначения — в виде равенств.
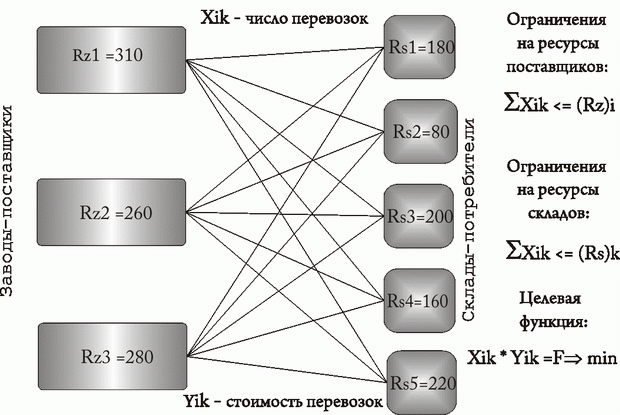
Нарисуем ментальную карту для данной задачи.
На рисунке введены следующие обозначения:
-
 — ресурс поставщика
— ресурс поставщика 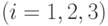 ;
; -
 — ресурс склада потребителя
— ресурс склада потребителя 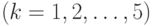 ;
; -
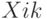 — число перевозок от
— число перевозок от  поставщика к
поставщика к  потребителю (целые числа);
потребителю (целые числа); -
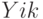 — стоимость одной перевозки от
— стоимость одной перевозки от  поставщика к
поставщика к  потребителю;
потребителю; -
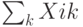 — число перевозок от
— число перевозок от  поставщика всем потребителям (суммируем по
поставщика всем потребителям (суммируем по  );
); -
 — число перевозок для
— число перевозок для  потребителя от всех поставщиков (суммируем по
потребителя от всех поставщиков (суммируем по  ).
).
Математическая модель транспортной задачи сводится к заданию двух матриц 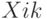 — число перевозок и
— число перевозок и 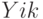 — стоимость
перевозок и двух векторов
— стоимость
перевозок и двух векторов
 — ресурс поставщика и
— ресурс поставщика и  — ресурс потребителя. Целевая функция определяет транспортные издержки потребителей,
которые должны быть
минимальными
— ресурс потребителя. Целевая функция определяет транспортные издержки потребителей,
которые должны быть
минимальными
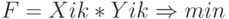
Множество допустимых решений ограничивается ресурсами поставщиков и ресурсами потребителей:
 — число перевозок от
— число перевозок от  поставщика всем потребителям не может превышать
производственных возможностей завода;
поставщика всем потребителям не может превышать
производственных возможностей завода;
 - число перевозок для
- число перевозок для  потребителя от всех поставщиков не может превышать
возможностей потребителя складировать привезенные товары.
потребителя от всех поставщиков не может превышать
возможностей потребителя складировать привезенные товары.
Для решения задачи средствами MS Excel нам нужно на листе книги представить дополнительно к матрице нормированных тарифов 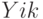 матрицу числа
перевозок
матрицу числа
перевозок 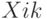 и сформировать целевую функцию в виде суммарных издержек потребителей. Подготовленные таблицы будут выглядеть следующим
образом:
и сформировать целевую функцию в виде суммарных издержек потребителей. Подготовленные таблицы будут выглядеть следующим
образом:
В качестве начальных значений элементов матрицы 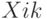 выбрано число 1. Целевая функция помещена в ячейку G16.
В ячейки второй таблицы вставлены
следующие формулы:
выбрано число 1. Целевая функция помещена в ячейку G16.
В ячейки второй таблицы вставлены
следующие формулы:
В ячейки D15:F16 вставлены формулы, аналогичные формулам В15:С16.
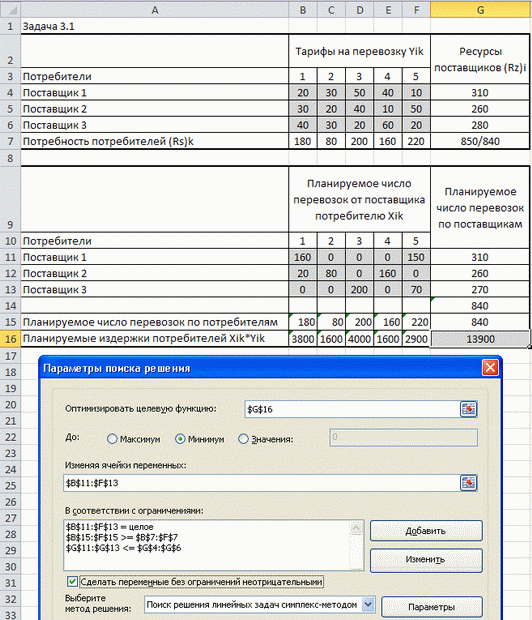
Заполнив данными поля диалогового окна "Параметры поиска решения" и введя ограничения, получим оптимальное решение транспортной задачи:
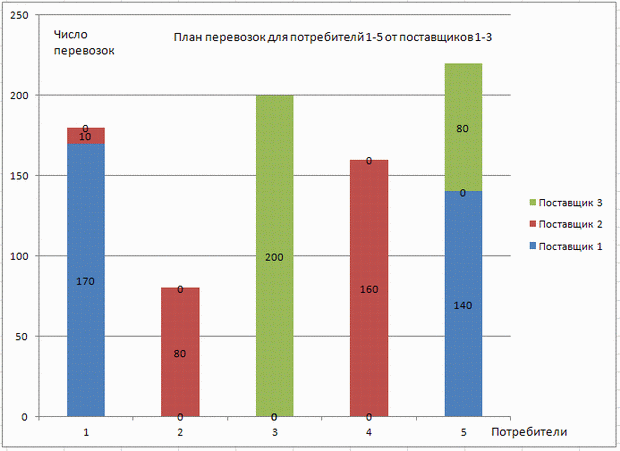
Из таблицы видно, что у поставщика 3 остаются возможности еще для 10 перевозок. Чтобы наглядно представить себе распределение перевозок между поставщиками и потребителями, построим диаграмму плана перевозок:
Оптимальность решения математической модели достигается по совокупным издержкам всех потребителей. Однако при принятии по данным результатам управленческого решения стоит обратить внимание на непропорциональность издержек полученному товару для разных потребителей. В самом деле, потребитель 1 получил 180 единиц товара и заплатил 3800 руб., а потребитель 5 получил больше — 220 единиц товара, а заплатил меньше — 2900 руб. Потребитель 2 получил товара вдвое меньше, чем потребитель 4, а заплатили одинаково — по 1600 руб.
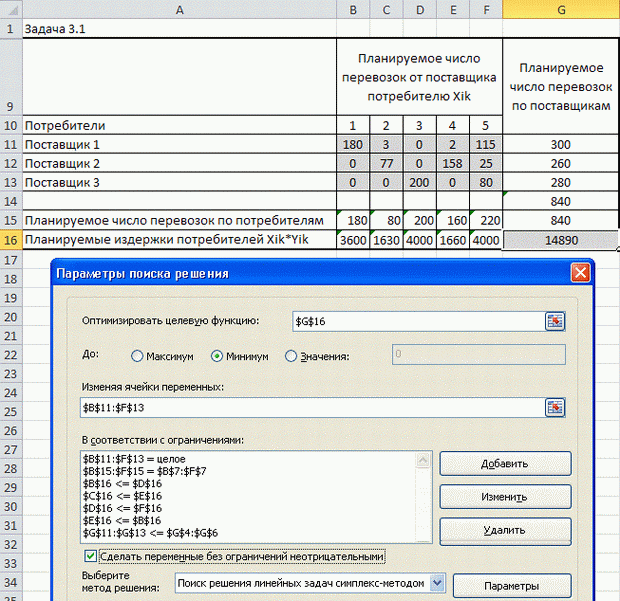
Если потребители относятся к разным фирмам, то они могут не согласиться на такую схему оплаты. Поэтому введем в параметры поиска решения дополнительные ограничения, отсортировав затраты в соответствии с количеством полученного товара. В результате поиска программа выдает такие результаты:
Заданные ограничения выполняются, но общие издержки возрастают на 990 руб.
К классу транспортных задач относятся также задачи о назначениях. Такие задачи возникают при определении маршрутов, при распределении людей на работы и должности, при распределении групп по аудиториям и пр.