Решение транспортных задач

Задача 3.2. Назначение бригад на работы

Требуется построить три объекта Oбj . К работе могут быть привлечены три бригады Брi 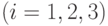. Каждая бригада из-за ограниченности своих ресурсов может одновременно строить только один объект. Каждый объект из-за технологических особенностей может строиться только одной бригадой. Известны сметные стоимости, которые установлены бригадой для объекта. Эти суммы (в тыс. руб.) приведены в матрице затрат :

Требуется разработать оптимальное по стоимости распределение бригад работников по объектам обслуживания.

Создадим ментальную карту по условиям задачи:

увеличить изображение

На связях бригад с объектами указаны нормативные коэффициенты — суммы, запрашиваемые бригадами за строительство объектов. Для удобства сравнения бригад между собой справа приведены суммарные стоимости работ каждой бригады для всех трех объектов. Из рисунка сразу видно, что Бригада 3 имеет наименьшие суммарные затраты. Но мы вынуждены учитывать ограничения по назначениям на работы: одна бригада может строить только один объект.

Математическая модель должна включать в себя три матрицы:

• матрицу назначений ;
• матрицу нормативных коэффициентов ;
• матрицу затрат .

Бинарные элементы матрицы назначений бригад на объекты равны 1, если бригада обслуживает объект и равны нулю в противоположном случае. При этом каждая бригада может одновременно обслуживать только один объект, и каждый объект может обслуживаться только одной бригадой. Поэтому сумма чисел по строкам и столбцам матрицы равна 1.

— матрица нормативных коэффициентов (тыс. руб.). Это матрица констант — они не меняются в процессе решения задачи.

Матрица затрат должна быть получена перемножением матрицы назначений на матрицу нормативных коэффициентов:

,;.

На листе книги таблицы выглядят следующим образом:

В ячейки матриц X и Z вставлены формулы:

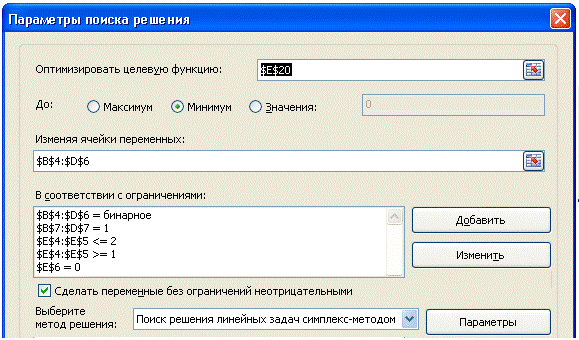
В качестве целевой функции выбираем общие затраты (ячейка Е20). Целью решения является минимизация этой функции.

По команде Данные — Поиск решения вызываем надстройку "Поиск решения". Диалоговое окно вместе с результирующими данными показано на рисунке.

увеличить изображение

Суммарные затраты 228 тыс. руб. являются оптимальными при таком распределении работ по объектам:

• бригада 1 строит объект Об1;
• бригада 2 строит объект Об2;
• бригада 3 строит объект Об3.

Интересно, что в данной задаче имеется несколько оптимальных решений. Непосредственно из матрицы затрат видно, что суммарные затраты также равны 228 тыс. руб. и при некоторых других распределениях работ по объектам.

Часто оптимальное решение математической модели не может быть воплощено в практику по самым разным причинам. Поэтому необходимо при планировании проводить вариантный анализ задачи, просчитывая возможные осложнения. Предположим, в частности, что самая "дешевая" бригада 3 нашла себе срочную другую работу и пока не может быть назначена на наши объекты. Но бригада 2 и бригада 3 увеличили свои ресурсы и имеют возможность строить по два объекта. Какой же бригаде поручить строить два объекта?

В этом варианте решения изменятся лишь ограничения на сумму бинарных коэффициентов. Для бригады 1 и бригады 2 эта сумма может быть равной 1 или 2, а для бригады 3 эта сумма равна 0:

Решение будет выглядеть следующим образом:

Бригада 1 будет строить объект Об2, а бригада 2 будет строить два объекта: Об1 и Об3. Но наши расходы в этом варианте возрастут на 10 000 руб.