| Почему область решений была взята как многоугольник ОАВС. А как же точки (567;0) и (0;320). На мой взгляд, я бы выбрал многоугольник с точками О (567;0) (0;320). Ведь они являются областью пересечения двух ограничений |
Графический метод оптимизации линейных моделей
Вычисляя теперь расстояния от жилых массивов до торгового центра, легко проверить, что целевая функция
— суммарное расстояние
переходов — имеет минимум в точке  . Оптимальное решение данной задачи задает координаты
торгового центра:
. Оптимальное решение данной задачи задает координаты
торгового центра:  ,
,  .
.
Из приведенных примеров видно, что областью допустимых решений линейных задач оптимизации является выпуклый многоугольник, в одной из вершин которого находится оптимальное решение. Оптимизация линейных моделей в MS Excel производится симплекс-методом — целенаправленным перебором опорных решений задачи линейного программирования. Алгоритм симплекс-метода сводится к построению выпуклого многогранника в многомерном пространстве, а затем к перебору его вершин с целью поиска экстремального значения целевой функции.
Эффективные средства линейного программирования лежат в основе и целочисленного и нелинейного программирования для решения более сложных задач оптимизации. Эти методы, однако, требуют более длительного времени для вычислений.
В последующих лекциях будут подробно разобраны примеры решения типичных задач оптимизации и принятия управленческих решений с помощью надстройки MS Excel "Поиск решения". Задачи, которые лучше всего решаются данным средством, имеют три основных свойства:
- имеется единственная цель, функционально связанная с другими параметрами системы, которую нужно оптимизировать (найти ее максимум, минимум или определенное числовое значение);
- имеются ограничения, выражающиеся, как правило, в виде неравенств (например, объем используемого сырья не может превышать запасов сырья на складе, или время работы станка за сутки не должно быть больше 24 часов минус время на обслуживание);
- имеется набор входных значений-переменных, влияющих на оптимизируемые величины и на ограничения.
Параметры задач ограничиваются такими предельными показателями:
- количество неизвестных – 200;
- количество формульных ограничений на неизвестные – 100;
- количество предельных условий на неизвестные – 400.
Алгоритм поиска оптимальных решений включает в себя несколько этапов:
Последовательность необходимых подготовительных работ, выполняемых при решении задач экономико-математического моделирования с помощью MS Excel, приведена на блок-схеме рисунка 1.6.
Из приведенных пяти пунктов плана подготовительных работ только пятый пункт является формализуемым. Остальные работы требуют творчества — и разными людьми они могут быть выполнены по-разному. Кратко поясним сущность формулировок пунктов плана.
- Определение структуры, постановка задачи требует четкости в задании обоснованных значений констант, переменных и целей. Нужно заранее видеть возможные варианты и до начала работы сформулировать цели дальнейшего анализа решения. Как говорил Цицерон, "Кто ясно мыслит, тот ясно излагает".
- Под "составлением формализованной модели" здесь понимается графическое описание задачи в виде схемы или рисунка. Такое описание аналогично составлению блок-схем алгоритма программы. Хорошим представлением условий задачи могут служить ментальные карты, построение которых описано в курсе [1]. Следует учитывать, что картинка всегда информативнее текста, а мышление человека осуществляется образами, а не буквами и словами.
- Математическая модель деятельности рассматриваемой реальной системы сводится к связыванию формулами отдельных элементов этой системы. В предыдущем примере мы выразили через формулы расход трудовых и материальных ресурсов, а целевую функцию выразили через заданные константы нормативного расхода и нормативной прибыли.
- Представление математической модели в виде таблицы MS Excel также должно отвечать требованиям ясности представления задачи. В таблице следует
четко выделять области:
область переменных
 ;
;область исходных нормированных коэффициентов
 ;
;область целевых коэффициентов
Следует давать наименования столбцам и строкам, а также ставить знаки неравенств в области ограничений. ;
; - В диалоге "Поиск решений" мы задаем программе оптимизации алгоритм цели. Пусть
 — заданное число исходных элементов,
— заданное число исходных элементов,
 — заданное число ресурсов. В предыдущем примере
— заданное число ресурсов. В предыдущем примере 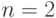 , — это полки типа
, — это полки типа  и полки типа
и полки типа  , а
, а  , —
мы учитывали только
ресурс
сырья (доски) и ресурс машинного времени.
, —
мы учитывали только
ресурс
сырья (доски) и ресурс машинного времени.
При постановке задачи известны целевые коэффициенты  и нормированные коэффициенты
и нормированные коэффициенты 
 .
В предыдущем примере коэффициентами, формирующими целевую функцию, служили значения нормированной прибыли на одну полку типа
.
В предыдущем примере коэффициентами, формирующими целевую функцию, служили значения нормированной прибыли на одну полку типа  (
( ) и одну полку типа
) и одну полку типа  (
( ). Нормированными коэффициентами
). Нормированными коэффициентами
 служили нормы расхода
материала и машинного времени на одну полку каждого типа. Матрица
служили нормы расхода
материала и машинного времени на одну полку каждого типа. Матрица  имела следующий вид:
имела следующий вид:
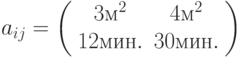
Кроме того, всегда известны значения ресурсов 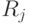 . В предыдущем примере это был
недельный запас досок и возможности использовать
машинное время:
. В предыдущем примере это был
недельный запас досок и возможности использовать
машинное время:  ,
,  . Часто в задачах значения переменных
. Часто в задачах значения переменных  требуется
ограничить. Поэтому нужно определить нижний
требуется
ограничить. Поэтому нужно определить нижний  и верхний
и верхний 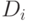 пределы области их изменений.
пределы области их изменений.
Таким образом, в диалоговом окне оптимизационной программы "Поиск решения" мы должны задать следующий целевой алгоритм:
 - целевая функция равна произведению вектора искомых значений переменных
- целевая функция равна произведению вектора искомых значений переменных
 на вектор целевых коэффициентов
на вектор целевых коэффициентов 
 - нормированных коэффициентов
- нормированных коэффициентов
 на вектор искомых значений переменных
на вектор искомых значений переменных  не должен превышать значения заданного вектора
ресурсов
не должен превышать значения заданного вектора
ресурсов 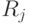
 - значения переменной
- значения переменной  должны находиться в заданных пределах
должны находиться в заданных пределах
 число исходных элементов системы
число исходных элементов системы
 - число исходных элементов системы
- число исходных элементов системы
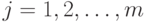 - число заданных видов ресурсов
- число заданных видов ресурсов
Отладка решения необходима в случае, когда программа выдает сообщение об отрицательных результатах (рисунок 1.7):
При отладке рекомендуется возвращаться к заданию новых начальных условий:
- если не получено допустимое решение, то выполнить корректировку модели исходных данных;
- если не получено оптимальное решение, то ввести дополнительные ограничения.
Программа выдает оптимальное решение только для модели реальной проблемы, а не решение самой проблемы. При построении модели были сделаны различные упрощающие допущения реальной ситуации. Это позволило формализовать процесс, приближенно отобразив реальные количественные зависимости между параметрами системы и целью. А если реальные параметры будут отличаться от тех, которые заложены в модели, то как изменится решение? Чтобы узнать это, перед принятием управленческого решения проводят анализ решения модели.
Анализ оптимального решения, встроенный в программу, представляет собой заключительный этап математического моделирования экономических процессов. Он позволяет осуществить более глубокую проверку соответствия модели процессу, а также надежности оптимального решения. Он основывается на данных оптимального решения и отчетов, которые выдаются в "Поиске решения". Но он не исключает и не заменяет традиционного анализа плана с экономических позиций перед принятием управленческого решения.
Экономический анализ ставит перед собой следующие цели [2]:
- определение возможных последствий в системе в целом и ее элементах при изменении параметра модели;
- оценка устойчивости оптимального плана к изменению отдельных параметров задачи: если он не устойчив к изменению большинства параметров, снижается гарантия его выполнения и достижения рассчитанного оптимума;
- проведение вариантных расчетов и получение новых вариантов плана без повторного решения задачи от исходного базиса с помощью корректировки.
Возможные методы анализа представлены в схеме на рисунке 1.8.
После получения оптимального решения проводится его анализ по полученным отчетам. Анализ устойчивости — изучение влияния изменений отдельно взятых параметров модели на показатели оптимального решения. Анализ пределов — анализ допустимых изменений в оптимальном плане, при котором план остается оптимальным.
Учитывая ответственность принятия экономического управленческого решения, руководитель должен убедиться, что полученный оптимальный план является единственно верным. Для этого надо на основе модели получить ответы на следующие вопросы:
- "что будет, если…"
- "что надо, чтобы…"
Анализ с целью ответа на первый вопрос называется вариантным анализом; анализ с целью ответа на второй вопрос называется решениями по заказу.
Вариантный анализ бывает следующих видов:
- Параметрический — анализ, который заключается в решении задачи при различных значениях некоторого параметра.
- Структурный анализ — когда решение задачи оптимизации ищется при различной структуре ограничений.
- Многокритериальный анализ — это решение задачи по разным целевым функциям.
- Анализ при условных исходных данных — когда исходные данные, используемые при решении задачи, зависят от соблюдения дополнительных условий.
После проведения анализа следует представить результаты в графической форме и составить отчет с рекомендациями о принятии решения с учетом конкретной экономической ситуации.
Ключевые термины
Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.
Математическая модель — приближенное описание объекта, выраженное с помощью математической символики, отражающее количественные соотношения между его элементами.
Симплекс-метод — вычислительная процедура, основанная на принципе последовательного улучшения решений.
Целевая функция — функция, связывающая цель (оптимизируемую переменную) с управляемыми переменными в задаче оптимизации.
Матрица нормированных коэффициентов — постоянные параметры объекта моделирования.
Ресурс— количественная мера возможности выполнения какой-либо деятельности; условия, позволяющие с помощью определённых преобразований получить желаемый результат.
Область допустимых решений — все решения, которые удовлетворяют заданным ограничениям задачи.
Оптимальное решение — допустимое решение, для которого значение целевой функции максимально.
Анализ решения — заключительный этап математического моделирования экономических процессов.
Краткие итоги
Графическое решение задач оптимизации удобно применять в случае двух искомых переменных. Тогда за декартовые координаты  и
и
 принимают
значения этих переменных. Если по физическому смыслу переменные могут быть только положительными, то решение ищется только в первом квадранте.
Линейные ограничения на заданные ресурсы выражаются в виде прямых линий. Эти линии вместе с осями координат
ограничивают
область допустимых
решений в виде выпуклого многоугольника. Оптимальное решение с экстремумом
целевой функции находится в одной из вершин многоугольника.
Координаты этой вершины являются искомыми значениями переменных.
принимают
значения этих переменных. Если по физическому смыслу переменные могут быть только положительными, то решение ищется только в первом квадранте.
Линейные ограничения на заданные ресурсы выражаются в виде прямых линий. Эти линии вместе с осями координат
ограничивают
область допустимых
решений в виде выпуклого многоугольника. Оптимальное решение с экстремумом
целевой функции находится в одной из вершин многоугольника.
Координаты этой вершины являются искомыми значениями переменных.
Вопросы
- Сформулируйте в общем виде задачу линейного программирования.
- Что такое симплекс-метод решения задач оптимизации?
- Что называется областью допустимых решений?
- Какие решения называются оптимальными?
- Как определить, по какую сторону от ограничительной прямой линии находится область допустимых решений?
- Что такое прямая уровня?
- Является ли оптимальное решение единственным?
- Как провести анализ решения?


 .
.
