| Почему область решений была взята как многоугольник ОАВС. А как же точки (567;0) и (0;320). На мой взгляд, я бы выбрал многоугольник с точками О (567;0) (0;320). Ведь они являются областью пересечения двух ограничений |
Графический метод оптимизации линейных моделей
Задача 1.2. Приготовление смесей
Для птицефабрики требуется составить самый дешевый рацион питания цыплят в виде смеси из корма  и корма
и корма  .
Цыплята должны получить
необходимую дозу витамина В1 — тиамина и витамина С — аскорбина при достаточной калорийности питания. Сколько надо взять граммов
корма
.
Цыплята должны получить
необходимую дозу витамина В1 — тиамина и витамина С — аскорбина при достаточной калорийности питания. Сколько надо взять граммов
корма  и корма
и корма  для каждой порции оптимальной смеси, чтобы удовлетворить потребность цыплят в витаминах и питательности корма?
для каждой порции оптимальной смеси, чтобы удовлетворить потребность цыплят в витаминах и питательности корма?
Исходные данные для поиска решения приведены в таблице:
| Тиамин, мг | Аскорбин, мг | Калории, кал | Цена, руб. | |
|---|---|---|---|---|
| Корм А, г | 0,1 | 1 | 110 | 3,80р. |
| Корм Б, г | 0,25 | 0,25 | 120 | 4,20р. |
| Потребность | 1 | 5 | 400 |
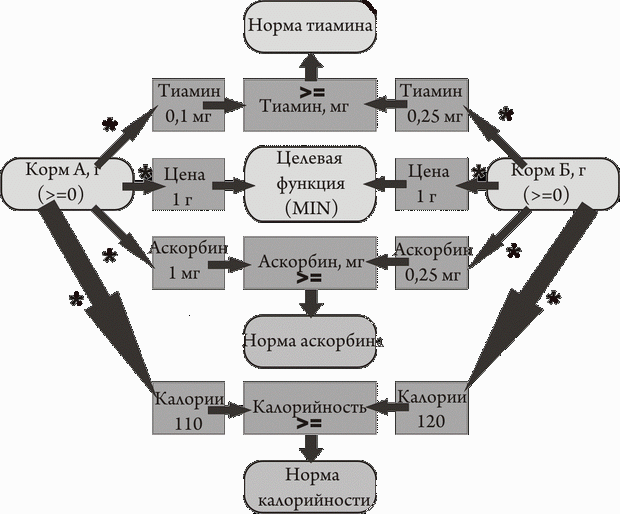
Для наглядного представления представим условия задачи в виде ментальной карты.
Математическая модель строится с искомыми переменными величинами — количеством  корма
корма  и количеством
и количеством  корма
корма  для каждой
порции оптимальной смеси. С учетом целевых коэффициентов — цены кормов — они определяют целевую функцию — издержки производства на
одну порцию корма для цыплят:
для каждой
порции оптимальной смеси. С учетом целевых коэффициентов — цены кормов — они определяют целевую функцию — издержки производства на
одну порцию корма для цыплят:
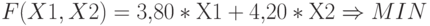
Оптимальному решению отвечает минимум целевой функции при следующих ограничениях:
 |
( 1) |
 |
( 2) |
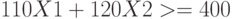 |
( 3) |
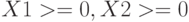 |
( 4) |
 и
и  не могут быть отрицательными.
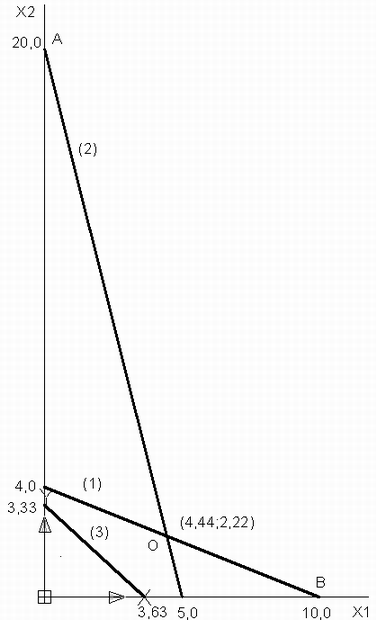
не могут быть отрицательными.Так как в данной задаче только две переменные, то вначале определим решение графически. В декартовой системе координат
 ,
,  построим прямые, соответствующие условиям (1), (2), (3).
построим прямые, соответствующие условиям (1), (2), (3).
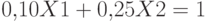 ;
;
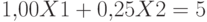 ;
;
 .
.
В соответствии с ограничением (4) мы должны рассматривать только область первого квадранта. Подставляя в условия (1) – (3)
значения начала координат 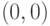 , находим, что область допустимых значений
ограничена осями координат и линиями
, находим, что область допустимых значений
ограничена осями координат и линиями  и
и 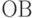 .
При этом все допустимые решения заведомо удовлетворяют условию (3) — по калорийности питания. Координаты вершины
.
При этом все допустимые решения заведомо удовлетворяют условию (3) — по калорийности питания. Координаты вершины  многоугольника
соответствуют оптимальному решению, т.е. минимальной стоимости одной порции корма.
многоугольника
соответствуют оптимальному решению, т.е. минимальной стоимости одной порции корма.
Результаты графического решения:
- 4,44 г количество корма А в одной порции оптимальной смеси;
- 2,22 г количество корма Б в одной порции оптимальной смеси;
- 26,22 руб. стоимость одной порции оптимальной смеси.