НОУ ИНТУИТ | Intel Parallel Programming Professional (Introduction). Лекция 7: Умножение разреженных матриц

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Нижегородский государственный университет им. Н.И.Лобачевского

Опубликован: 02.10.2012 | Доступ: свободный | Студентов: 1754 / 201 | Длительность: 17:47:00

Темы: Программирование, Суперкомпьютерные технологии

Специальности: Программист

Теги: Intel Parallel Studio, высокопроизводительные вычисления, кластеры, многозадачность, распараллеливание

|

Вам нравится? Нравится 148 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Приложение. Моделирование и анализ параллельных вычислений

При разработке параллельных алгоритмов решения сложных научнотехнических задач принципиальным моментом является анализ эффективности использования параллелизма, состоящий обычно в оценке получаемого ускорения процесса вычислений (сокращения времени решения задачи). Формирование подобных оценок ускорения может осуществляться применительно к выбранному вычислительному алгоритму (оценка эффективности распараллеливания конкретного алгоритма). Другой важный подход может состоять в построении оценок максимально возможного ускорения процесса решения задачи конкретного типа (оценка эффективности параллельного способа решения задачи).

В данной главе описывается модель вычислений в виде графа "операции-операнды", которая может использоваться для описания существующих информационных зависимостей в выбираемых алгоритмах решения задач, приводятся оценки эффективности максимально возможного параллелизма, которые могут быть получены в результате анализа имеющихся моделей вычислений. Примеры использования излагаемого теоретического материала приводятся при рассмотрении параллельных алгоритмов в завершающих разделах настоящего учебного материала.

Модель вычислений в виде графа "операции–операнды"

Для описания существующих информационных зависимостей в выбираемых алгоритмах решения задач может быть использована модель в виде графа "операции–операнды" Для уменьшения сложности излагаемого материала при построении модели будет предполагаться, что время выполнения любых вычислительных операций является одинаковым и равняется 1 (в тех или иных единицах измерения). Кроме того, принимается, что передача данных между вычислительными устройствами выполняется мгновенно без какихлибо затрат времени (что может быть справедливо, например, при наличии общей разделяемой памяти в параллельной вычислительной системе).

Представим множество операций, выполняемых в исследуемом алгоритме решения вычислительной задачи, и существующие между операциями информационные зависимости в виде ациклического ориентированного графа

$G=\left(V,R\right)$

где $V=\lbrace 1,\ldots, \left|V\right|\rbrace$ есть множество вершин графа, представляющих выполняемые операции алгоритма, а R есть множество дуг графа (при этом дуга $r=\left(i,j\right)$ принадлежит графу только в том случае, если операция j использует результат выполнения операции i). Для примера на рис. p.1 показан граф алгоритма вычисления площади прямоугольника, заданного координатами двух противолежащих углов. Как можно заметить по приведенному примеру, для выполнения выбранного алгоритма решения задачи могут быть использованы разные схемы вычислений и построены соответственно разные вычислительные модели. Как будет показано далее, разные схемы вычислений обладают различными возможностями для распараллеливания и, тем самым, при построении модели вычислений может быть поставлена задача выбора наиболее подходящей для параллельного исполнения вычислительной схемы алгоритма.

В рассматриваемой вычислительной модели алгоритма вершины без входных дуг могут использоваться для задания операций ввода, а вершины без выходных дуг – для операций вывода. Обозначим через $\overline V$ множество вершин графа без вершин ввода, а через $d\left(G\right)$ диаметр (длину максимального пути) графа.

Описание схемы параллельного выполнения алгоритма

Операции алгоритма, между которыми нет пути в рамках выбранной схемы вычислений, могут быть выполнены параллельно (для вычислительной схемы на рис. p.1 , например, параллельно могут быть реализованы сначала все операции умножения, а затем первые две операции вычитания). Возможный способ описания параллельного выполнения алгоритма может состоять в следующем.

Пусть p есть количество процессоров, используемых для выполнения алгоритма. Тогда для параллельного выполнения вычислений необходимо задать множество (расписание)

$H_p=\lbrace\left(i,P_i,t_i\right):i\in V\rbrace$

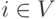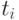в котором для каждой операции $i\in V$ указывается номер используемого для выполнения операции процессора P_i и время начала выполнения операции t_i . Для того, чтобы расписание было реализуемым, необходимо выполнение следующих требований при задании множества H_p :

Рис. p.1. Пример вычислительной модели алгоритма в виде графа "операции-операнды"

$\forall i,j\in V : t_i=t_j\Longrightarrow P_i\neq P_j$ , т. е. один и тот же процессор не должен назначаться разным операциям в один и тот же момент времени,
$\forall \left(i,j\right)\in R\Longrightarrow t_j\geq t_i+1$ , т. е. к назначаемому моменту выполнения операции все необходимые данные уже должны быть вычислены.

Определение времени выполнения параллельного алгоритма

Вычислительная схема алгоритма G совместно с расписанием H_p может рассматриваться как модель параллельного алгоритма $A_p\left(G,H_p\right)$ , исполняемого с использованием p процессоров. Время выполнения параллельного алгоритма определяется максимальным значением времени, используемым в расписании

$T_p\left(G,H_p\right)=\max\limits_{i\in V}\left(t_i+1\right)$

Для выбранной схемы вычислений желательно использование расписания, обеспечивающего минимальное время исполнения алгоритма

$T_p\left(G\right)=\min\limits_{H_p}T_p\left(G,H_p\right)$

Уменьшение времени выполнения может быть обеспечено и путем подбора наилучшей вычислительной схемы

$T_p=\min\limits_{G}T_p\left(G\right)$

Оценки $T_p\left(G,H_p\right)$ , $T_p\left(G\right)$ и T_p могут быть использованы в качестве показателей времени выполнения параллельного алгоритма. Кроме того, для анализа максимально возможного параллелизма можно определить оценку наиболее быстрого исполнения алгоритма

$T_\infty=\min\limits_{p\geq 1}T_p$

Оценку $T_\infty$ можно рассматривать как минимально возможное время выполнения параллельного алгоритма при использовании неограниченного количества процессоров (концепция вычислительной системы с бесконечным количеством процессоров, обычно называемой паракомпьютером, широко используется при теоретическом анализе параллельных вычислений).

Оценка 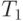T_1 определяет время выполнения алгоритма при использовании одного процессора и представляет, тем самым, время выполнения последовательного варианта алгоритма решения задачи. Построение подобной оценки является важной задачей при анализе параллельных алгоритмов, поскольку она необходима для определения эффекта использования параллелизма (ускорения времени решения задачи). Очевидно, что

$T_1\left(G\right)=\left|\overline{V}\right|$

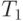где $\left|\overline{V}\right|$ , напомним, есть количество вершин вычислительной схемы G без вершин ввода. Важно отметить, что если при определении оценки T_1 ограничиться рассмотрением только одного выбранного алгоритма решения задачи и использовать величину

$T_1=\min\limits_{G}T_1\left(G\right)$

то получаемые при использовании такой оценки показатели ускорения будут характеризовать эффективность распараллеливания выбранного алгоритма. Для оценки эффективности параллельного решения исследуемой задачи вычислительной математики время последовательного решения следует определять с учетом различных последовательных алгоритмов, т. е. использовать величину

$T_{1}^*=\min T_1$

где операция минимума берется по множеству всех возможных последовательных алгоритмов решения данной задачи.

Приведем без доказательства теоретические положения, характеризующие свойства оценок времени выполнения параллельного алгоритма.

Теорема 1. Минимально возможное время выполнения параллельного алгоритма определяется длиной максимального пути вычислительной схемы алгоритма, т. е.

$T_\infty\left(G\right)=d\left(G\right)$

Теорема 2. Пусть для некоторой вершины вывода в вычислительной схеме алгоритма существует путь из каждой вершины ввода. Кроме того, пусть входная степень вершин схемы (количество входящих дуг) не превышает 2. Тогда минимально возможное время выполнения параллельного алгоритма ограничено снизу значением

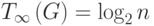
$T_\infty\left(G\right)=\log_2n$

где n есть количество вершин ввода в схеме алгоритма.

Теорема 3. При уменьшении числа используемых процессоров время выполнения алгоритма увеличивается пропорционально величине уменьшения количества процессоров, т. е.

$\forall q=cp, 0<c<1\Longrightarrow T_p\leq cT_q$

Теорема 4. Для любого количества используемых процессоров справедлива следующая верхняя оценка для времени выполнения параллельного алгоритма

$\forall p\Longrightarrow T_p<T_\infty +\frac{T_1}{p}$

Теорема 5. Времени выполнения алгоритма, которое сопоставимо с минимально возможным временем $T_\infty$ , можно достичь при количестве процессоров порядка $p\sim \frac{T_1}{T_\infty}$ , а именно,

$p\geq T_1/ T_\infty\Longrightarrow T_p\leq 2T_\infty$

При меньшем количестве процессоров время выполнения алгоритма не может превышать более, чем в 2 раза, наилучшее время вычислений при имеющемся числе процессоров, т. е.

$p<T_1/T_\infty\Longrightarrow\frac{T_1}{p}\leq T_p\leq 2\frac{T_1}{p}$

Приведенные утверждения позволяют дать следующие рекомендации по правилам формирования параллельных алгоритмов:

при выборе вычислительной схемы алгоритма должен использоваться граф с минимально возможным диаметром (см. теорему 1);
для параллельного выполнения целесообразное количество процессоров определяется величиной $p \sim T_1 /T_\infty$ (см. теорему 5);
время выполнения параллельного алгоритма ограничивается сверху величинами, приведенными в теоремах 4 и 5.

Для вывода рекомендаций по формированию расписания по параллельному выполнению алгоритма приведем доказательство теоремы 4.

Доказательство теоремы 4. Пусть $H_\infty$ есть расписание для достижения минимально возможного времени выполнения $T_\infty$ . Для каждой итерации $\tau$ , $0\leq\tau\leq T_\infty$ , выполнения расписания $H_\infty$ обозначим через $n_\tau$ количество операций, выполняемых в ходе итерации $\tau$ . Расписание выполнения алгоритма с использованием p процессоров может быть построено следующим образом. Выполнение алгоритма разделим на $T_\infty$ шагов; на каждом шаге $\tau$ следует выполнить все $n_\tau$ операций, которые выполнялись на итерации $\tau$ расписания $H_\infty$ . Выполнение этих операций может быть выполнено не более, чем за $\lceil n_\tau/ p\rceil$ итераций при использовании p процессоров. Как результат, время выполнения алгоритма T_p может быть оценено следующим образом

$T_p=\sum\limits_{\tau=1}^{T_\infty}\lceil\frac{n_\tau}{p}\rceil<\sum\limits_{\tau=1}^{T_\infty}\left(\frac{n_\tau}{p}+1\right)=\frac{T_1}{p}+T_\infty$

Доказательство теоремы дает практический способ построения расписания параллельного алгоритма. Первоначально может быть построено расписание без учета ограниченности числа используемых процессоров (расписание для паракомпьютера). Затем, согласно схеме вывода теоремы, может быть построено расписание для конкретного количества процессоров.

Дальше >>

Авторизоваться

Intel Parallel Programming Professional (Introduction)

Умножение разреженных матриц

Приложение. Моделирование и анализ параллельных вычислений

Модель вычислений в виде графа "операции–операнды"

Описание схемы параллельного выполнения алгоритма

Определение времени выполнения параллельного алгоритма

Вопросы и ответы