|
поддерживаю выше заданые вопросы
|
Умножение разреженных матриц
7. Итерационные методы решения СЛАУ
В данном разделе мы рассмотрим методы решения систем линейных уравнений, принципиально отличающиеся от прямых методов поиска точного решения, рассмотренных в предыдущем разделе. Пусть
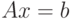 |
( 7.49) |
 с
симметричной положительно определенной матрицей
с
симметричной положительно определенной матрицей  размерности
размерности  и правой частью вектором
и правой частью вектором  Точное решение системы (7.49) обозначим
через
Точное решение системы (7.49) обозначим
через 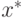
Итерационный метод , предназначенный для решения системы (7.49), генерирует последовательность векторов  ,
,  каждый из которых может рассматриваться исследователем как приближенное решение
системы (7.49). Начальное приближение – вектор
каждый из которых может рассматриваться исследователем как приближенное решение
системы (7.49). Начальное приближение – вектор 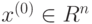 – задает исследователь. Итерационный метод называется сходящимся , если для любого
начального приближения
– задает исследователь. Итерационный метод называется сходящимся , если для любого
начального приближения 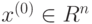 последовательность
последовательность  ,
,  сходится к точному решению
сходится к точному решению 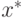 , т.е.
, т.е.
 |
( 7.50) |
 обозначена любая векторная норма.
обозначена любая векторная норма.На практике используют два критерия остановки итерационных методов одновременно: остановку по точности и остановку по числу итераций. Первый критерий определяется условием
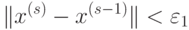 |
( 7.51) |
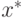 – приближение, полученное на итерации с номером
– приближение, полученное на итерации с номером  ,
, 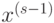 – приближение, полученное на предыдущей итерации. Параметр точности метода
– приближение, полученное на предыдущей итерации. Параметр точности метода 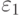 задает исследователь. Если условие (7.51) выполнено, метод завершает работу и вектор
задает исследователь. Если условие (7.51) выполнено, метод завершает работу и вектор  трактуется как приближенное решение системы (7.49). Величина
трактуется как приближенное решение системы (7.49). Величина 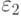 , определяемая как
, определяемая как  |
( 7.52) |
Второй критерий определяется максимальным числом итераций  , на которое готов пойти исследователь. Если номер итерации, которую предстоит выполнить, превышает
, на которое готов пойти исследователь. Если номер итерации, которую предстоит выполнить, превышает  N, итерация не выполняется, метод завершает
работу, вектор
N, итерация не выполняется, метод завершает
работу, вектор 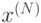 трактуется как приближенное решение системы и достигнутая точность метода
трактуется как приближенное решение системы и достигнутая точность метода  также сообщается исследователю.
также сообщается исследователю.
При изучении сходимости итерационных методов и при их реализации в
качестве векторной нормы  обычно используют евклидову норму
обычно используют евклидову норму  ,
,  , определяемую суммой модулей всех компонент вектора, норму
, определяемую суммой модулей всех компонент вектора, норму 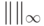 ,определяемую максимальным модулем компоненты, а также
энергетическую норму
,определяемую максимальным модулем компоненты, а также
энергетическую норму  , порождаемую симметричной, положительно определенной матрицей
, порождаемую симметричной, положительно определенной матрицей  . Так как в конечномерных нормированных пространствах указанные нормы эквивалентны, для доказательства сходимости метода или для его реализации можно пользоваться любой из перечисленных
норм.
. Так как в конечномерных нормированных пространствах указанные нормы эквивалентны, для доказательства сходимости метода или для его реализации можно пользоваться любой из перечисленных
норм.
Метод простой итерации
Последовательный алгоритм
Метод простой итерации относится к классу явных стационарных
одношаговых итерационных методов решения линейных систем вида с симметричной положительно определенной матрицей  . Метод определяется формулой
. Метод определяется формулой 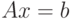 с симметричной положительно определенной матрицей
с симметричной положительно определенной матрицей  . Метод определяется формулой
. Метод определяется формулой

 – текущее приближение,
– текущее приближение, 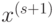 – следующее приближение,
– следующее приближение, 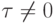 – фиксированное число, являющееся параметром метода.
– фиксированное число, являющееся параметром метода.Формула для вычисления нового приближения по предыдущему может быть записана в виде

 – невязка приближения с номером
– невязка приближения с номером 
Далее нетрудно записать явные формулы для отыскания компонент нового
вектора 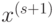 :
:

Справедлива следующая теорема о сходимости: если матрица  симметрична и положительно определена и параметр метода
симметрична и положительно определена и параметр метода  лежит в интервале
лежит в интервале  , где
, где  - максимальное собственное число матрицы
- максимальное собственное число матрицы  , метод сходится к точному решению системы (7.49) с любого начального приближения. Известно, что оптимальным значением параметра
, метод сходится к точному решению системы (7.49) с любого начального приближения. Известно, что оптимальным значением параметра  является значение
является значение

 и
и  – минимальное и максимальное собственные числа матрицы
– минимальное и максимальное собственные числа матрицы
 соответственно.
соответственно.Напомним, что погрешностью приближения с номером  называют вектор
называют вектор
 , определяемый как
, определяемый как
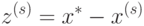
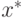 – точное решение системы
– точное решение системы 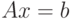 . Для метода простой итерации с оптимальным параметром справедлива следующая оценка:
. Для метода простой итерации с оптимальным параметром справедлива следующая оценка: 
Здесь через  обозначена среднеквадратичная норма вектора,
обозначена среднеквадратичная норма вектора,  через
через 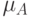 – число обусловленности матрицы
– число обусловленности матрицы  , согласованное с векторной нормой
, согласованное с векторной нормой  и в силу этого вычисляемое как
и в силу этого вычисляемое как 
Оценим трудоемкость предложенного алгоритма. Анализ расчетных формул показывает, что они включают одну операцию умножения матрицы на вектор и три операции над векторами (сложение, вычитание, умножение на константу). Общее количество операций, выполняемых на одной итерации, составляет

Таким образом, выполнение  итераций метода потребует
итераций метода потребует
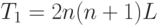
Параллельный алгоритм
При распараллеливании итерационных методов линейной алгебры (в частности, метода простой итерации) в первую очередь следует учесть, что выполнение итераций метода осуществляется последовательно и, тем самым, наиболее целесообразный подход состоит в распараллеливании вычислений, реализуемых в ходе выполнения итераций.
Анализ последовательного алгоритма показывает, что основные затраты на
 -й итерации – порядка
-й итерации – порядка 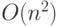 операций – состоят в умножении матрицы
операций – состоят в умножении матрицы  на вектор текущего приближения
на вектор текущего приближения  . Как результат, при организации параллельных вычислений могут быть использованы известные методы параллельного умножения матрицы на вектор (например, параллельный алгоритм матрично-векторного умножения при ленточном горизонтальном
разделении матрицы). Дополнительные вычисления, имеющие порядок
сложности
. Как результат, при организации параллельных вычислений могут быть использованы известные методы параллельного умножения матрицы на вектор (например, параллельный алгоритм матрично-векторного умножения при ленточном горизонтальном
разделении матрицы). Дополнительные вычисления, имеющие порядок
сложности  , представляют собой операции сложения и умножение на
скаляр для векторов. Организация таких вычислений также может быть
выполнена в многопоточном режиме.
, представляют собой операции сложения и умножение на
скаляр для векторов. Организация таких вычислений также может быть
выполнена в многопоточном режиме.
Несмотря на простоту распараллеливания, данный метод редко применяется, т.к. он обладает существенно меньшей скоростью сходимости по сравнению с иными методами, к рассмотрению которых мы переходим.
Метод верхней релаксации
Рассмотрим систему (7.49) с симметричной, положительно определенной
матрицей  размера
размера  . Обозначим через
. Обозначим через  диагональную матрицу
диагональную матрицу  такую, что ее главная диагональ совпадает с главной диагональю матрицы
такую, что ее главная диагональ совпадает с главной диагональю матрицы
 . Через
. Через  обозначим нижнюю треугольную матрицу
обозначим нижнюю треугольную матрицу  такую, что ее
ненулевые (поддиагональные) элементы также совпадают с элементами
такую, что ее
ненулевые (поддиагональные) элементы также совпадают с элементами  ,
а главная диагональ является нулевой. Аналогично обозначим через
,
а главная диагональ является нулевой. Аналогично обозначим через  верхнюю треугольную матрицу
верхнюю треугольную матрицу  , ненулевые (наддиагональные) элемен-
ты которой совпадают с элементами
, ненулевые (наддиагональные) элемен-
ты которой совпадают с элементами  , а главная диагональ также является
нулевой. В этом случае для
, а главная диагональ также является
нулевой. В этом случае для  справедливо представление в виде
справедливо представление в виде
 |
( 7.5) |
 |
( 7.54) |
 – приближение, полученное на итерации с номером
– приближение, полученное на итерации с номером  ,
, 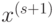 – следующее приближение,
– следующее приближение,  – число (параметр метода), матрицы
– число (параметр метода), матрицы и вектор
и вектор  определены выше.
определены выше.Необходимым условием сходимости метода релаксации с любого начального приближения 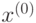 к точному решению задачи
к точному решению задачи 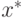 является выполнение
условия
является выполнение
условия  . Если же матрица
. Если же матрица  симметрична и положительно определена, то выполнение данного условия является также и достаточным. При
этом если
симметрична и положительно определена, то выполнение данного условия является также и достаточным. При
этом если  , то говорят о методе нижней релаксации , а при
, то говорят о методе нижней релаксации , а при
 - о методе верхней релаксации , при
- о методе верхней релаксации , при 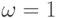 метод релаксации
будет совпадать с известным методом Зейделя .
метод релаксации
будет совпадать с известным методом Зейделя .
Скорость сходимости метода верхней релаксации определяется выбором
параметра  . Известно [4], что при решении некоторых классов разреженных систем уравнений, метод Зейделя требует
. Известно [4], что при решении некоторых классов разреженных систем уравнений, метод Зейделя требует 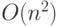 итераций, а при
надлежащем выборе итерационного параметра
итераций, а при
надлежащем выборе итерационного параметра  метод будет сходиться за
метод будет сходиться за
 итераций.
итераций.
В общем случае нет аналитической формулы для вычисления оптимального параметра  , обеспечивающего наилучшую сходимость. Например,
для решения систем уравнений, возникающих при аппроксимации дифференциальных уравнений в частных производных, можно использовать эвристические оценки вида
, обеспечивающего наилучшую сходимость. Например,
для решения систем уравнений, возникающих при аппроксимации дифференциальных уравнений в частных производных, можно использовать эвристические оценки вида
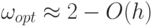
 – шаг сетки, на которой проводилась дискретизация.
– шаг сетки, на которой проводилась дискретизация.В некоторых случаях можно более точно оценить оптимальный параметр. Известной оценкой [17] является выражение
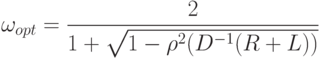
 – спектральный радиус матрицы, а
– спектральный радиус матрицы, а 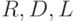 – из (7.53). Возникающий
при этом вопрос об оценке спектрального радиуса может быть решен численно, например, при помощи степенного метода [2].
– из (7.53). Возникающий
при этом вопрос об оценке спектрального радиуса может быть решен численно, например, при помощи степенного метода [2].Также следует отметить, что для ряда задач, возникающих при решении задач математической физики методом сеток, оптимальные параметры метода верхней релаксации найдены аналитически.
Последовательный алгоритм
Получим формулы для отыскания 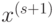 по предыдущему приближению
по предыдущему приближению  в явном виде.
в явном виде.

С учетом того, что 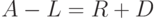 , получаем
, получаем

Далее нетрудно записать явные формулы для отыскания компонент нового
вектора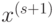 :
:
 |
( 7.55) |
Как следует из формулы (7.55), при подсчете  -й компоненты нового приближения все компоненты, индекс которых меньше
-й компоненты нового приближения все компоненты, индекс которых меньше  , берутся из нового
приближения
, берутся из нового
приближения 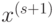 , а все компоненты, индекс которых больше либо равен
, а все компоненты, индекс которых больше либо равен  – из старого приближения
– из старого приближения  . Таким образом, после того, как
. Таким образом, после того, как  -я компонента нового приближения вычислена,
-я компонента нового приближения вычислена,  -я компонента старого приближения нигде использоваться не будет. Напротив, для подсчета следующих
компонент вектора
-я компонента старого приближения нигде использоваться не будет. Напротив, для подсчета следующих
компонент вектора 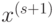 компоненты с индексом, меньшим или равным
компоненты с индексом, меньшим или равным  ,
будут использоваться "в новой версии". В силу этого обстоятельства для
реализации метода достаточно хранить только одно (текущее) приближение
,
будут использоваться "в новой версии". В силу этого обстоятельства для
реализации метода достаточно хранить только одно (текущее) приближение  , а при расчете следующего приближения
, а при расчете следующего приближения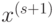 использовать формулу (7.55) для всех компонент по порядку и постепенно обновлять вектор
использовать формулу (7.55) для всех компонент по порядку и постепенно обновлять вектор  .
.
Организация параллельных вычислений
При распараллеливании метода верхней релаксации также применим подход, который состоит в распараллеливании вычислений, реализуемых в ходе выполнения итераций.
Анализ последовательного алгоритма показывает, что основные затраты на
 -й итерации – порядка
-й итерации – порядка  операций – заключаются в операциях матричного умножения
операций – заключаются в операциях матричного умножения  и
и 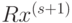 . Однако напрямую распараллелить эти
операции не представляется возможным, т.к. в методе верхней релаксации
не только итерации осуществляются последовательно, но и вычисление
компонент вектора очередного приближения
. Однако напрямую распараллелить эти
операции не представляется возможным, т.к. в методе верхней релаксации
не только итерации осуществляются последовательно, но и вычисление
компонент вектора очередного приближения 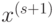 также осуществляется
последовательно, начиная с первой.
также осуществляется
последовательно, начиная с первой.
Применение ленточного разделения данных, аналогично методу простой итерации, приведет к изменению вычислительной схемы алгоритма. Поэтому одним из возможных способов распараллеливания, сохраняющем в точности последовательность действий метода, состоит в распараллеливании операций, необходимых для получения одной компоненты вектора нового приближения. При этом распараллелить можно вычисление сумм в формуле (7.55).

