|
После приведения формулы вида ПНФ к виду ССФ вы получаете формулу, в безквантовой матрице которой дизъюнкт содержит оба контранрных атома: |
Множества
В данной лекции мы попробуем реализовать некоторое приближение математического понятия "множество" в Прологе. Заметим, что в Прологе, в отличие от некоторых императивных языков программирования, нет такой встроенной структуры данных, как множество. И, значит, нам придется реализовывать это понятие, опираясь на имеющиеся стандартные домены. В качестве базового домена используем стандартный списковый домен, с которым мы работали на протяжении двух последних лекций.
Итак, что мы будем понимать под множеством? Просто список, который не содержит повторных вхождений элементов. Другими словами, в нашем множестве любое значение не может встречаться более одного раза.
На самом деле я не знаю ни одной реализации понятия множества, которая бы достаточно точно соответствовала этому математическому объекту. Наше подобие множества также, по большому счету, лишь отчасти будет приближаться к "настоящему" множеству.
Нам предстоит разработать предикаты, которые реализуют основные теоретико-множественные операции.
Начнем с написания предиката, превращающего произвольный список во множество, в том смысле, в котором мы договорились понимать этот термин. Для этого нужно удалить все повторные вхождения элементов. При этом мы воспользуемся предикатом delete_all, который был создан нами ранее, в седьмой лекции. Предикат будет иметь два аргумента: первый — исходный список (возможно, содержащий повторные вхождения элементов), второй — выходной (то, что остается от первого аргумента после удаления повторных вхождений элементов).
Предикат будет реализован посредством рекурсии. Базисом рекурсии является очевидный факт: в пустом списке никакой элемент не встречается более одного раза. По правде говоря, в пустом списке нет ни одного элемента, который встречался бы в нем хотя бы один раз, то есть в нем вообще нет элементов. Шаг рекурсии позволит выполнить правило: чтобы сделать из непустого списка множество (в нашем понимании этого понятия), нужно удалить из хвоста списка все вхождения первого элемента списка, если таковые вдруг обнаружатся. После выполнения этой операции первый элемент гарантированно будет встречаться в списке ровно один раз. Для того чтобы превратить во множество весь список, остается превратить во множество хвост исходного списка. Для этого нужно только рекурсивно применить к хвосту исходного списка наш предикат, удаляющий повторные вхождения элементов. Полученный в результате из хвоста список с приписанным в качестве головы первым элементом и будет требуемым результатом ( множеством, т.е. списком, образованным элементами исходного списка и не содержащим повторных вхождений элементов).
Закодируем наши рассуждения.
list_set([],[]). /* пустой список является множеством
в нашем понимании */
list_set ([H|T],[H|T1]) :–
delete_all(H,T,T2),
/* T2 — результат удаления
вхождений первого элемента
исходного списка H из хвоста T */
list_set (T2,T1).
/* T1 — результат удаления
повторных вхождений элементов
из списка T2 */Например, если применить этот предикат к списку [1,2,1,2,3, 2,1], то результатом будет список [1,2,3].
Заметим, что в предикате, обратном только что записанному предикату list_set и переводящем множество в список, нет никакой необходимости по той причине, что наше множество уже является списком.
Теперь займемся реализацией теоретико-множественных операций, таких как принадлежность элемента множеству, объединение, пересечение, разность множеств и т.д.
При реализации этих предикатов можно было бы воспользоваться предикатами, предназначенными для работы с обыкновенными списками, но в результате их применения могут получаться списки, содержащие некоторые элементы несколько раз, даже если исходные списки были множествами, в нашем понимании этого слова.
Можно, конечно, после каждого применения теоретико-множественной операции превращать полученный список обратно во множество применением вышеописанного предиката list_set, но это было бы не очень удобно. Вместо этого мы попробуем написать каждую из теоретико-множественных операций так, чтобы в результате ее работы гарантированно получалось множество.
Итак, приступим.
В качестве реализации операции принадлежности элемента множеству вполне можно использовать предикат member3, который мы разработали в седьмой лекции, когда только начинали знакомиться со списками. Напомним, что факт принадлежности элемента x множеству A в математике принято обозначать следующим образом: 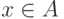 .
.
Для того чтобы найти мощность множества, вполне подойдет предикат length, рассмотренный нами в седьмой лекции. Напомним, что для конечного множества мощность — это количество элементов во множестве .
Пример. Реализуем операцию объединения двух множеств. На всякий случай напомним, что под объединением двух множеств понимают множество, элементы которого принадлежат или первому, или второму множеству. Обозначается объединение множеств A и B через 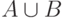 . В математической записи это выглядит следующим образом:
. В математической записи это выглядит следующим образом:  . На рисунке объединение множеств A и B обозначено штриховкой.
. На рисунке объединение множеств A и B обозначено штриховкой.
У соответствующего этой операции предиката должно быть три параметра: первые два — множества, которые нужно объединить, третий параметр — результат объединения двух первых аргументов. В третий аргумент должны попасть все элементы, которые входили в первое или второе множество. При этом нам нужно проследить, чтобы ни одно значение не входило в итоговое множество несколько раз. Такое могло бы произойти, если бы мы попытались, например, воспользоваться предикатом conc (который мы рассмотрели в седьмой лекции), предназначенным для объединения списков. Если бы какое-то значение встречалось и в первом, и во втором списках, то в результирующий список оно бы попало, по крайней мере, в двойном количестве. Значит, вместо использования предиката conc нужно написать новый предикат, применение которого не приведет к ситуации, в которой итоговый список уже не будет множеством за счет того, что некоторые значения будут встречаться в нем более одного раза.
Без рекурсии мы не обойдемся и здесь. Будем вести рекурсию по первому из объединяемых множеств. Базис индукции: объединяем пустое множество с некоторым множеством. Результатом объединения будет второе множество. Шаг рекурсии будет реализован посредством двух правил. Правил получается два, потому что возможны две ситуации: первая — голова первого множества является элементом второго множества, вторая — первый элемент первого множества не входит во второе множество. В первом случае мы не будем добавлять голову первого множества в результирующее множество, она попадет туда из второго множества. Во втором случае ничто не мешает нам добавить первый элемент первого списка. Так как этого значения во втором множестве нет, и в хвосте первого множества оно также не может встречаться (иначе это было бы не множество ), то и в результирующем множестве оно также будет встречаться только один раз.
Давайте запишем эти рассуждения:
union([ ],S2,S2). /* результатом объединения
пустого множества со множеством S2
будет множество S2 */
union([H|T],S2,S):–
member3(H,S2),
/* если голова первого
множества H принадлежит второму
множеству S2, */
!,
union(T,S2,S).
/* то результатом S будет
объединение хвоста первого
множества T и второго
множества S2 */
union([H |T],S2,[H|S]):–
union(T,S2,S).
/* в противном случае результатом
будет множество, образованное
головой первого множества H
и хвостом, полученным объединением
хвоста первого множества T
и второго множества S2 */Если объединить множество [1,2,3,4] со множеством [3,4,5], то в результате получится множество [1,2,3,4,5].


 . Как тогда проводить его унификацию, если в случае замены x на f(x) весь дизъюнкт обратится в единицу?
. Как тогда проводить его унификацию, если в случае замены x на f(x) весь дизъюнкт обратится в единицу?