|
После приведения формулы вида ПНФ к виду ССФ вы получаете формулу, в безквантовой матрице которой дизъюнкт содержит оба контранрных атома: |
Логические основы Пролога
Эта лекция будет посвящена теоретическим основам языка Пролог. В принципе, вполне можно писать хорошие программы на языке Пролог, не вдаваясь в глубины математической логики. И в этом смысле можно считать эту главу необязательной, факультативной. Однако тем, кому интересно узнать, "как она вертится", мы попробуем объяснить, как устроен Пролог, на чем он основывается.
Давайте начнем с самого начала или почти с самого начала, раз уж мы договорились, что никаких предварительных навыков от слушателей не требуется. Нам придется попытаться разобраться с понятиями логики первого порядка, которая лежит в основе Пролога; они обычно изучаются в курсе математической логики. Конечно, для того чтобы изучить даже самые начала математической логики, одной лекции недостаточно. Поэтому мы попытаемся пробежаться только по тому кусочку, который имеет отношение к языку Пролог. Часть используемых нами понятий все-таки останется "за кадром".
Говорят, что задана некая формальная система F, если определены:
- алфавит системы — счетное множество символов;
- формулы системы — некоторое подмножество всех слов, которые можно образовать из символов, входящих в алфавит (обычно задается процедура, позволяющая составлять формулы из символов алфавита системы);
- аксиомы системы — выделенное множество формул системы;
- правила вывода системы — конечное множество отношений между формулами системы.
Зададим логику первого порядка (или логику предикатов), на которой основывается Пролог. Язык логики предикатов — один из формальных языков, наиболее приближенных к человеческому языку.
Алфавит логики первого порядка составляют следующие символы:
- переменные (будем обозначать их последними буквами английского алфавита u, v, x, y, z );
- константы (будем обозначать их первыми буквами английского алфавита a, b, c, d );
- функциональные символы (используем для их обозначения ближние буквы f и g );
- предикатные символы (обозначим их дальними буквами p, q и r );
- пропозициональные константы истина и ложь ( true и false );
- логические связки
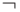 (отрицание),
(отрицание),  (конъюнкция),
(конъюнкция),  (дизъюнкция),
(дизъюнкция),  (импликация);
(импликация); - кванторы:
 (существования),
(существования), 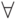 (всеобщности);
(всеобщности); - вспомогательные символы (, ), ,.
Всякий предикатный и функциональный символ имеет определенное число аргументов. Если предикатный (функциональный) символ имеет n аргументов, он называется n -местным предикатным (функциональным) символом.
Термом будем называть выражение, образованное из переменных и констант, возможно, с применением функций, а точнее:
- всякая переменная или константа есть терм;
- если t1,...,tn — термы, а f — n -местный функциональный символ,то f(t1,...,tn) — терм;
- других термов нет.
По сути дела, все объекты в программе на Прологе представляются именно в виде термов.
Если терм не содержит переменных, то он называется основным или константным термом.
Атомарная или элементарная формула получается путем применения предиката к термам, точнее, это выражение p(t1,...,tn), где p — n -местный предикатный символ, а t1,...,tn — термы.
Формулы логики первого порядка получаются следующим образом:
- всякая атомарная формула есть формула;
- если A и B — формулы, а x — переменная, то выражения
 (читается "не A" или "отрицание A"),
(читается "не A" или "отрицание A"),  (читается "A и B"),
(читается "A и B"), 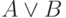 (читается "A или B"), A -> B (читается "A влечет B"),
(читается "A или B"), A -> B (читается "A влечет B"), 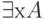 (читается "для некоторого x" или "существует x") и
(читается "для некоторого x" или "существует x") и  (читается "для любого x" или "для всякого x")– формулы;
(читается "для любого x" или "для всякого x")– формулы; - других формул нет.
В случае, если формула имеет вид  или
или 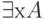 , ее подформула A называется областью действия квантора
, ее подформула A называется областью действия квантора 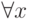 или
или  соответственно. Если вхождение переменной x в формулу находится в области действия квантора
соответственно. Если вхождение переменной x в формулу находится в области действия квантора 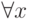 или
или  , то оно называется связанным вхождением. В противном случае, вхождение переменной в формулу называется свободным.
, то оно называется связанным вхождением. В противном случае, вхождение переменной в формулу называется свободным.
Чтобы не увеличивать чрезмерно объем лекции, мы не будем рассматривать полный список аксиом и правил вывода логики первого порядка.Те из них, которые пригодятся нам в дальнейшем, будут приведены в соответствующих местах.
Литералом будем называть атомарную формулу или отрицание атомарной формулы. Атом называется положительным литералом, а его отрицание — отрицательным литералом.
Дизъюнкт — это дизъюнкция конечного числа литералов. Если дизъюнкт не содержит литералов, его называют пустым дизъюнктом и обозначают посредством символа 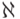 .
.
Давайте посмотрим, как можно привести любую формулу к множеству дизъюнктов, с которым работает метод резолюций. Для этого нам понадобятся некоторые определения нормальных форм.
Говорят, что формула находится в конъюнктивной нормальной форме,если это конъюнкция конечного числа дизъюнктов. Имеет место теорема о том, что для любой бескванторной формулы существует формула, логически эквивалентная исходной и находящаяся в конъюнктивной нормальной форме.
Формула находится в предваренной (или префиксной ) нормальной форме, если она представлена в виде Q1x1,..., QnxnA, где Qi — это квантор 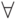 или
или 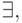 а формула A не содержит кванторов. Выражение Q1x1,..., Qnxn называют префиксом, а формулу A — матрицей.
а формула A не содержит кванторов. Выражение Q1x1,..., Qnxn называют префиксом, а формулу A — матрицей.
Формула находится в сколемовской нормальной форме, если она находится в предваренной нормальной форме и не содержит кванторов существования.

 . Как тогда проводить его унификацию, если в случае замены x на f(x) весь дизъюнкт обратится в единицу?
. Как тогда проводить его унификацию, если в случае замены x на f(x) весь дизъюнкт обратится в единицу?