НОУ ИНТУИТ | Модели и смыслы данных в Cache и Oracle. Лекция 7: Языки реляционных баз данных

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Кубанский государственный университет

Опубликован: 24.12.2013 | Доступ: свободный | Студентов: 681 / 8 | Длительность: 24:28:00

Тема: Базы данных

Специальности: Администратор баз данных

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

7.3 Исчисление высказываний

Определение. Высказывание — это утверждение, которое имеет однозначно определенное значение истинности. Высказывание в логике предикатов — это формула, все переменные которой связаны кванторами.

Заметьте, что нас по-прежнему не волнует смысл. Иначе говоря, исчисление дает форму, в которой могут быть сделаны правильные выводы, то есть утверждает, что из набора ППФ можно (или нельзя) построить заданную ППФ. И ничего более.

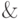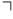Определение. Символы исчисления высказываний — это символы высказываний А,В,С, ..., символы значений истинности Т,_1_ и символы логических связок $\vee$ , $\&$ , $\urcorner$ , $\Rightarrow$ .

Определение. Правильно построенные формулы (ППФ):

символ высказывания или значения истинности есть ППФ;
отрицание ППФ есть ППФ;
конъюнкция и дизъюнкция ППФ есть ППФ;
импликация одной ППФ в другую ППФ есть ППФ.

Системы аксиом исчисления высказываний (например, аксиоматика Кли-ни) хорошо исследованы, но мы их не рассматриваем, так как не будем строить доказательства, исходя из выбранной системы аксиом.

7.4 Исчисление предикатов

7.4.1 ППФ в исчислении предикатов

Логика высказываний расширяется до логики предикатов путем включения в формулы утверждений, являющихся предикатами. Естественно, появляются и предикатные переменные. Поэтому определение ППФ усложняется.

Определение (Терм).

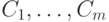переменные $X_1,\dots,X_n$ и константы $C_1,\dots,C_m$ — это термы;
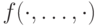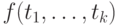если $f(\cdot,\dots,\cdot)$ — функция переменных, ставящая в соответствие изучаемым объектам другой объект, и $t_1,\dots,t_k$ —термы, то $f(t_1,\dots,t_k)$ —терм;

Определение (Формула).

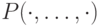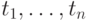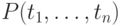если $P(\cdot,\dots,\cdot)$ — -местный предикат, а $t_1,\dots,t_n$ — термы, то $P(t_1,\dots,t_n)$ — (атомарная) формула;
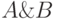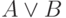если и — формулы, то $A\&B$ , $A\vee B$ , $A\Rightarrow B$ — формулы;
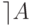если — формула, то $\rceil A$ — формула;
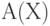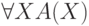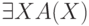если — формула, содержащая переменную , то $\forall X A(X)$ , $\exists X A(X)$ — формулы.

7.4.2 Замечание о функциональных символах

При внимательном прочтении приведенного выше определения терма должны возникнуть вопросы:

Чем функциональный символ отличается от предикатного символа?
А зачем вообще нужны функциональные символы?

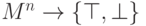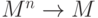Ответ на первый вопрос: -местный предикат на множестве задает отображение $M^n\to \{\top,\bot\}$ , а -местная функция определяет отображение $M^n\to M$ .

Ответ на второй вопрос: 0-местная функция 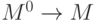$M^0\to M$ отождествляется с элементом множества . Не всегда удобно иметь отдельный символ для каждого элемента множества . Функциональные символы позволяют дать более сжатое представление. Например, фраза естественного языка "моя левая нога" может пониматься как существование левой ноги у субъекта "Я" и записываться как функция "ЛеваяНога(Я)", что позволяет не именовать по отдельности левые ноги всех людей.

Учтите, что за определенной таким образом функцией не предполагается никакой процедуры ее вычисления.

7.4.3 Определение узкого исчисления предикатов

Для определения узкого исчисления предикатов необходимо определить набор допустимых символов, правильно построенные формулы, набор аксиом и правила вывода.

Определение. Символы исчисления предикатов — это символы переменных, констант, функций и предикатов, символы значений истинности 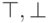$\top,\bot$ , символы логических связок 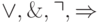$\vee ,\&, \urcorner, \Rightarrow$ и кванторы общности 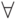$\forall$ и существования $\exists$ .

Правильно построенные формулы и входящие в них термы определены выше. Набор аксиом включает аксиомы исчисления высказываний и следующие дополнительные аксиомы:

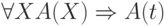
$\forall X A(X)\Rightarrow A(t)$
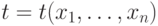$A(t)\Rightarrow\existsxA(x)$ , где $t=t(x_1,\dots,x_n)$ - терм и в формуле A нет кванторов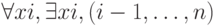 $\forall xi,\exists xi,(i-1,\dots,n)$

Дополнительные правила вывода:

Если 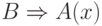$B\Rightarrow A(x)$ , то $B\Rightarrow \forallxA(x)$
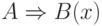Если $A\Rightarrow B(x)$ , то $\forallxA(x)\Rightarrow B$ .

К дополнительным правилам вывода относят еще "исключение &", "введение &" и "универсальное инстанцирование".

Определение. "Исключение &" —это вывод истинности обоих конъюнктов и и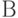з истинности $А\&В$ .

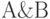Определение. "Введение &" — это вывод истинности 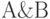$А\&В$ из истинности обоих конъюнктов А и В.

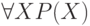Определение (Правило универсального инстанцирования). Если любую переменную, стоящую под квантором всеобщности, заменить на любой терм из области определения, то полученное выражение истинно. Например, если терм А принадлежит той же области определения, что , и $\forall XP(X)$ , то выводимо Р(А) .

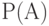7.4.4 Порядок исчисления предикатов

Исчисление первого порядка: В исчислении первого порядка можно связывать знаком квантора только переменные, но не функции или предикаты.

Исчисление высших порядков: В исчислении предикатов высших порядков можно связывать знаком квантора не только переменные, но и функции и предикаты.

Пусть требуется найти отношение, в котором имеется заданный атрибут 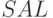SAL . Это запрос в логике второго порядка. Ему соответствует формула:

$\exists Р ~ (SAL~ есть предикатная переменная в Р)$

в которой квантор навешен на имя предиката Р.

В рамках реляционной теории можно работать только с кортежами, но не с отношениями. В реализациях баз данных существует словарь. Это база метаданных, обычно реляционного типа. Словарь содержит сведения о созданных таблицах, их столбцах, ограничениях целостности и т.д. В реляционной модели данных словарь не предполагается. В этом одно из существенных различий между реляционной моделью и моделями данных реальных СУБД. Именно наличие словаря позволяет писать запросы в логике второго порядка.

Прикладное исчисление предикатов: В такое исчисление введены дополнительные знаки констант, функций, операций, предикатов и дополнительные аксиомы, связывающие эти новые знаки.

Пример: Исчисление предикатов с равенством.

Дальше >>

Авторизоваться

Модели и смыслы данных в Cache и Oracle

Языки реляционных баз данных