Инструменты Gnumeric для статистиков

5.3 Корреляция

Корреляционный анализ, как известно, позволяет выявить взаимосвязь двух случайных величин. Коэффициент корреляции (корреляция по Пирсону) может принимать значения от -1 до 1. Чем ближе к 1 абсолютная величина коэффициента корреляции, тем сильнее связаны исследуемые случайные величины.

Для примера рассмотрим несколько выборок. Первая выборка (назовем ее "Выборка1") является нормально распределенной случайной величиной со средним значением 5 и стандартным отклонением 1, вторая ("Выборка2") – также нормально распределенная случайная величина со средним значением 4 и стандартным отклонением 2, третья ("Выборка3") – случайная величина с однородным распределением в интервале . Четвертая выборка ("Выборка4") получена путем удвоения значений Выборки1 и добавления к результату десятой доли значений Выборки3 (т.е. Выборка4=2*Выборка1+Выборка3/10) в каждой точке.

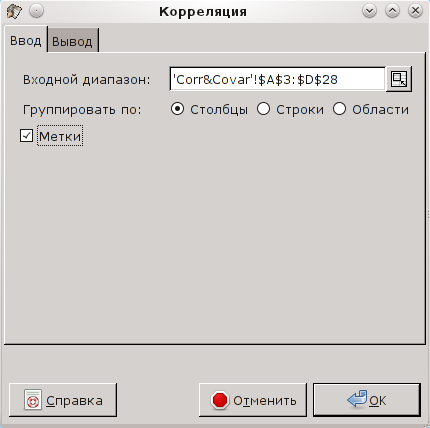
Пусть в каждой выборке будет по 25 значений, и начинать генерацию исходных данных будем со столбца . После создания выборок вызовем диалог "Корреляция" ("Статистика/Описательные статистики/Корреляция...", рис. 5.12).

Присвоение имён столбцам исходных данных и использование режима "Метки" в диалоге "Корреляция" позволяет на выходе получить именованные результаты (рис. 5.13).

Видно, что каждая выборка сама с собой прекрасно коррелирует (коэффициент равен 1), а четвертая выборка с первой дает коэффициент почти равный 1 (почти, но не совсем, поскольку Выборка4 искажена дополнительным влиянием Выборки3).

Для упражнения полезно вычислить коэффициент корреляции двух независимых выборок случайных величин с одинаковыми параметрами распределения.

5.4 Ковариация

Коэффициент ковариации также позволяет определить взаимосвязи случайных величин, но, в отличие от коэффициента корреляции, этот параметр не является нормированным, поэтому его значение не несет никакой очевидной информации. Более информативным является вычисление коэффициента корреляции. Посмотрим на результаты вычисления ковариации ("Статистика/Описательные статистики/Ковариация...") для тех же исходных данных, что и в примере вычисления корреляции (рис. 5.14).

Рис. 5.12. Определение исходных данных для вычисления корреляции

Рис. 5.13. Результаты вычисления корреляции выборок

Рис. 5.14. Результат вычисления ковариации выборок

Видно, что без дополнительных усилий как-то интерпретировать результаты вычисления ковариации достаточно сложно.