НОУ ИНТУИТ | Электронная таблица Gnumeric. Лекция 6: Регрессионный анализ в Gnumeric

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 24.04.2015 | Доступ: свободный | Студентов: 146 / 0 | Длительность: 04:57:00

Темы: Офисные технологии, Программное обеспечение

Специальности: Менеджер, Математик, Преподаватель, Физик

|

Вам нравится? Нравится 7 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

6.1 Небольшое теоретическое введение

Всегда полезно знать, что и почему вычисляется в той или иной задаче. Поэтому сначала рассмотрим некоторые теоретические основы регрессионного анализа.

Линейный парный регрессионный анализ заключается в определении параметров эмпирической линейной зависимости (1), описывающей связь между некоторым числом пар значений x_i и y_i , обеспечивая при этом наименьшую среднеквадратическую погрешность (метод наименьших квадратов).

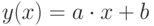$y(x)=a \cdot x+b$

( 6.1)

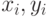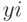Графически это выглядит как проведение прямой в "облаке" точек с координатами x_i, y_i так, чтобы величина всех отклонений между значениями y на этой прямой при имеющихся значениях и координатами имеющихся точек отвечала условию (6.2).

$U= \sum^N_{i=1}(y_i-y(x_i))^2 \to min$

( 6.2)

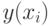где y(x_i) – теоретическая зависимость (6.1). Для этого нужно приравнять к нулю частные производные (6.3 и 6.4).

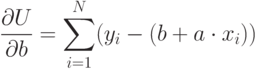$\frac{\partial U}{\partial b}= \sum^N_{i=1}(y_i-(b+a \cdot x_i))$

( 6.3)

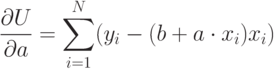$\frac{\partial U}{\partial a}= \sum^N_{i=1}(y_i-(b+a \cdot x_i)x_i)$

( 6.4)

Тогда для определения коэффициентов линейной регрессии и получаем систему уравнений (6.5).

$\left \begin{cases} b \cdot N+a \cdot \sum^N_{i=1}x_i=\sum^N_{i=1}y_i \\ b \cdot \sum^N_{i=1}x_i+a \cdot \sum^N_{i=1}x^2_i=\sum^N_{i=1}x_i \cdot y_i\\ \end{cases} \right$

( 6.5)

Решение этой системы даётся соотношениями 6.6 и 6.7.

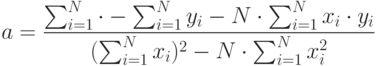$a= \frac{\sum^N_{i=1} \cdot - \sum^N_{i=1}y_i-N \cdot \sum^N_{i=1}x_i \cdot y_i}{(\sum^N_{i=1}x_i)^2-N \cdot \sum^N_{i=1}x^2_i}$

( 6.6)

$b= \frac{1}{N} \cdot \left(\sum^N_{i=1}y_i-a \cdot \sum^N_{i=1}x_i \right)$

Для определения отклонения связи между x_i и y_i от линейной используется коэффициент парной корреляции (6.8).

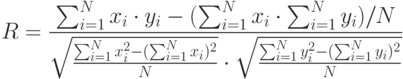$R= \frac{\sum^N_{i=1}x_i \cdot y_i-(\sum^N_{i=1}x_i \cdot \sum^N_{i=1}y_i)/N}{\sqrt{\frac{\sum^N_{i=1}x^2_i-(\sum^N_{i=1}x_i)^2}{N}} \cdot \sqrt{\frac{\sum^N_{i=1}y^2_i-(\sum^N_{i=1}y_i)^2}{N}}}$

( 6.8)

Если экспериментальная зависимость явно нелинейная, для её интерполяции (аппроксимации) применяются различные нелинейные зависимости (экспоненциальная, степенная с положительными или отрицательными показателями степени, полиномиальные различных порядков и пр.). При этом интерполяционная функция "линеаризуется", т. е. сводится к виду (6.1) путём замены переменных. Соответственно пересчитываются значения экспериментальных точек и коэффициент парной корреляции показывает успешность этого преобразования. Поскольку знак коэффициента парной корреляции при оценке качества линеаризации не является существенным, часто используется значение R^2 .

Дальше >>

Авторизоваться

Электронная таблица Gnumeric

Регрессионный анализ в Gnumeric

6.1 Небольшое теоретическое введение

Вопросы и ответы