Опубликован: 24.04.2015 | Доступ: свободный | Студентов: 146 / 0 | Длительность: 04:57:00
Специальности: Менеджер, Математик, Преподаватель, Физик
Лекция 7:
Линейная оптимизация (поиск решения)
Ключевые слова: функция, вектор, модуль, поиск, программирование, прибыль, таблица, меню, максимум, переключатель, ключ, ячейка, значение, алгоритм, сообщение об ошибке, objective
7.1 Оптимизация как задача линейного программирования
Всегда полезно, что и почему вычислятся в той или иной задаче. Поэтому сначала рассмотрим некотрые теоретические основы регрессионного анализа.
Пусть имеется функция, называемая целевой, линейно зависящая от некоторых переменных (факторов).
 |
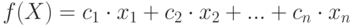( 7.1) |
В данном случае 
– вектор неизвестных (значений факторов).
 |
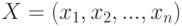( 7.2) |
Значения неизвестных находятся из системы m линейных ограничений, которая может содержать как уравнения, так и неравенства.
 |
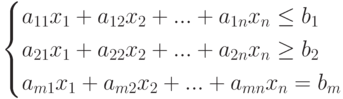( 7.3) |
При этом вводится дополнительное условие неотрицательности значений переменных.
 |
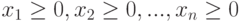( 7.4) |
Неотрицательное решение системы (7.3), то есть вектор при соблюдении условий (7.3) и (7.4), называется "планом задачи".
| Продукция Сырье | Продукт 1 | Продукт 2 | Запасы сырья |
|---|---|---|---|
| 1 | 5 | 9 | 45 |
| 2 | 3 | 9 | 19 |
| 3 | 2 | 1 | 10 |
| ПРИБЫЛЬ | 5 | 6 |
План X' называется оптимальным планом задачи максимизации (минимизации), если для любого плана X выполняется условие
 |
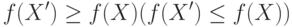( 7.5) |
Таким образом, поскольку решение задачи линейного программирования сводится к нахождению оптимального плана и вычислению максимального (минимального) значения целевой функции, такие задачи также называют задачами линейной оптимизации.
В современных офисных электронных таблицах для решения подобных задач имеется модуль "Solver" ("Поиск решения"). Далее рассмотри пример решения задачи линейной оптимизации в Gnumeric.
