|
При переходе на страницу 2 после изучения постоянных издержек, лекция сразу "говорит" о технологическом процессе. кроме того, в имеющейся лекции нет формул, задачи на которые в большом количестве представлены в тесте |
Финансовый план
Цель лекции. Научиться разрабатывать финансовый план и проводить его анализ.
9.1. Инвестиции и время
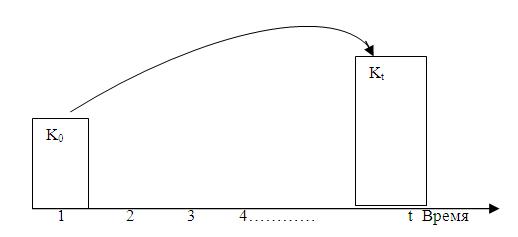
Одна из главных проблем при расчете инвестиций заключается в сопоставлении выплат, которые делаются в разные моменты времени. Одинаковые по величине доходы или затраты, осуществляемые в разное время, экономически неравнозначны. Когда фирма принимает решение о строительстве завода и закупке оборудования, она должна сравнить капиталовложения, которые ей предстоит сделать сейчас, с дополнительной прибылью, которую принесет новый капитал в будущем. Чтобы провести подобное сопоставление, фирма должна ответить на следующий вопрос: сколько будущие прибыли стоят сегодня? Расчеты текущей стоимости будущих доходов, а также другие межвременные инвестиционные решения принимаются с помощью операций по начислению сложных процентов и дисконтированию. Известно, что процесс роста основной суммы вклада за счет накопления процентов называется начислением сложного процента, а сумма, полученная в результате накопления процента, называется наращенной, или будущей стоимостью суммы вклада по истечении периода, за который осу ществляется расчет (Рис. 9.1). Первоначальная сумма вклада называется текущей стоимостью.
Если обозначить первоначальную сумму вклада через 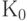 , будущую сумму в t-м году через
, будущую сумму в t-м году через  , ставку процента через
, ставку процента через  , число лет через
, число лет через  , получим будущую (наращенную) стоимость:
, получим будущую (наращенную) стоимость:
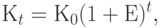 |
( 9.1) |
где  — коэффициент начисления сложных процентов
— коэффициент начисления сложных процентов 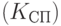 .
.
Предположим, что у вас есть 1 руб. и его можно инвестировать под процент  . По прошествии одного года вы получите 1 руб. плюс процент, заработанный на 1 руб. Тогда
. По прошествии одного года вы получите 1 руб. плюс процент, заработанный на 1 руб. Тогда 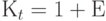 . Если повторить этот процесс в конце второго года, то
. Если повторить этот процесс в конце второго года, то 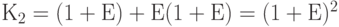 , а будущая стоимость 1 руб., инвестированного на
, а будущая стоимость 1 руб., инвестированного на  периодов, составит:
периодов, составит:
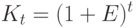
Если инвестировать не 1 руб., а 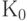 руб., то получим формулу (9.1).
руб., то получим формулу (9.1).
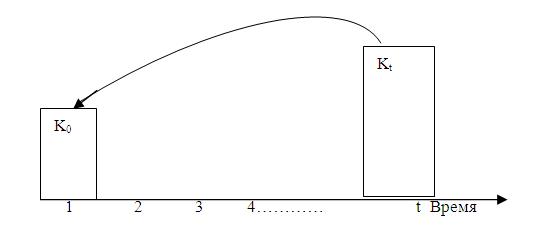
В финансовой практике часто сталкиваются с задачей, обратной определению наращенной суммы: по заданной сумме  , которую следует уплатить через некоторое время
, которую следует уплатить через некоторое время  , необходимо определить сумму полученной ссуды
, необходимо определить сумму полученной ссуды 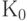 . В этом случае говорят, что сумма
. В этом случае говорят, что сумма  дисконтируется (Рис. 9.2).
дисконтируется (Рис. 9.2).
При помощи дисконтирования решается и сформулированная выше задача: сколько будущие прибыли стоят сегодня? Приведем формулу дисконтирования по ставкам сложных процентов:
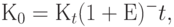 |
( 9.2) |
где 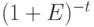 — дисконтный множитель за
— дисконтный множитель за  лет.
лет.
Величину 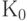 ,полученную дисконтированием
,полученную дисконтированием  часто называют текущей, современной (приведенной) величиной
часто называют текущей, современной (приведенной) величиной  . Она характеризует ту исходную (базовую) сумму, на которую начисление процентов дает величину
. Она характеризует ту исходную (базовую) сумму, на которую начисление процентов дает величину  . Поэтому коэффициент дисконтирования также называют коэффициентом текущей стоимости:
. Поэтому коэффициент дисконтирования также называют коэффициентом текущей стоимости:
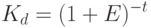
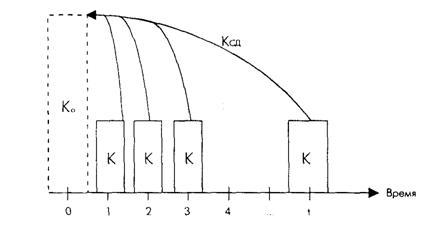
На практике часто дисконтируют и ряд платежей. Предположим, что имеем дело с арендой, причем платежи по годам одинаковые (Рис. 9.3).
Какова же наличная стоимость этих платежей? Речь идет о превращении платежного ряда в "разовый платеж сейчас". Техника такой операции следующая: надо привести каждый разовый платеж к моменту t = 0 и просуммировать полученные величины.
Величину 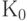 в этом случае называют суммой дисконтирования.
в этом случае называют суммой дисконтирования.
 |
( 9.3) |
Сумма дисконтированных множителей:
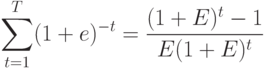
поэтому сумма дисконтирования
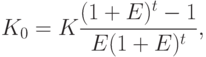 |
( 1.4) |
где  — постоянный платеж,
— постоянный платеж,  — коэффициент суммы дисконтирования.
— коэффициент суммы дисконтирования.
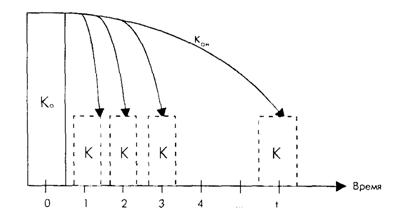
Аннуитет (от позднелат. annuitas — ежегодный платеж) — во-первых, это один из видов срочного займа, по которому ежегодно выплачиваются проценты и погашается часть суммы; во-вторых, так называют равные друг другу денежные платежи, выплачиваемые через определенные промежутки времени в счет погашения полученного кредита, займа, и проценты по нему.
Аннуитет рассчитывается с помощью коэффициента аннуитета ( ), который распределяет величину
), который распределяет величину 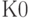 на равные суммы платежей (аннуитеты)
на равные суммы платежей (аннуитеты)  с учетом процента на
с учетом процента на  лет, т.е. превращает "разовый платеж сейчас" в платежный ряд (Рис. 9.4).
лет, т.е. превращает "разовый платеж сейчас" в платежный ряд (Рис. 9.4).
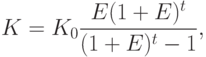 |
( 9.4) |
где 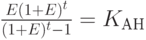 — коэффициент aннуитета.
— коэффициент aннуитета.
Срок службы большинства видов оборудования составляет, как правило, больше года. Фактические расходы на покупку инвестиционных товаров и срок их службы не совпадают в один и тот же период учета. Поэтому в целях недопущения занижения прибыли в период покупки, с одной стороны, и завышения прибыли в последующие годы, с другой, предприятия рассчитывают срок службы оборудования и распределяют общий объем стоимости инвестиционных товаров более или менее равномерно на весь срок службы оборудования. Ежегодные отчисления, которые показывают объем капитала, потребленного в ходе производства в отдельные годы, называются амортизацией. Ежегодные амортизационные отчисления определяются умножением стоимости основных фондов на норму амортизации или на коэффициент амортизационных отчислений. В бухгалтерской практике амортизационные отчисления определяются с помощью норм амортизации, установленных государством по отдельным элементам основных фондов. При проведении экономических инвестиционных расчетов, особенно когда объекты различаются по срокам службы, амортизация определяется с помощью рассчитываемых коэффициентов амортизации.
Если равномерно распределить амортизационные отчисления за срок службы объекта, то коэффициент амортизации будет определяться по формуле
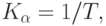 |
( 9.5) |
где  — срок службы объекта.
— срок службы объекта.
А.Л. Лурье предложил [36] для определения коэффициента амортизации другую формулу, учитывающую фактор времени:
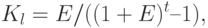 |
( 9.6) |
Сущность вывода формулы состоит в том, что сумма амортизационных отчислений должна быть равна восстановительной стоимости объекта. Таким образом, для определения амортизационных отчислений получено уравнение
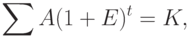
где  — годовая амортизация,
— годовая амортизация,  принимает значения
принимает значения 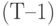 — для отчислений, производимых в конце первого года службы объекта,
— для отчислений, производимых в конце первого года службы объекта,  — для отчислений, производимых в конце второго года, и т.д. до
— для отчислений, производимых в конце второго года, и т.д. до  — для отчислений, производимых в последний год его службы. По формуле суммы членов геометрической прогрессии имеем
— для отчислений, производимых в последний год его службы. По формуле суммы членов геометрической прогрессии имеем
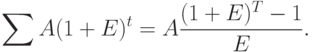
Отсюда:
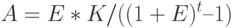
Если выразить величину амортизационных отчислений в долях от  , то
, то
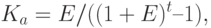 |
( 9.8) |
Приведем пример. Определить норму амортизационных отчислений с учетом и без учета фактора времени. Первоначальная стоимость машины К = 10 000 руб., срок службы машины Т — 5 лет, процентная ставка Е = 0,1.
Решение: Без учета фактора времени норма амортизационных отчислений составит:

Сумма амортизационных отчислений  за срок службы составит:
за срок службы составит:
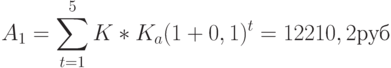
Рассчитаем норму амортизационных отчислений с учетом фактора времени по формуле (9.6):
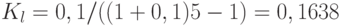
Сумма амортизационных отчислений за срок службы составит:
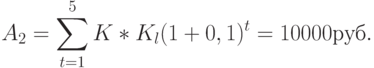
Этот пример наглядно показывает, что в инвестиционных инновационных расчетах, которые носят не бухгалтерский, а экономический характер амортизацию следует считать по формуле А. Лурье.