Основы Maxima
2.7.7 Преобразование тригонометрических выражений
Функция  раскладывает все тригонометрические и гиперболические функции от сумм и произведений в комбинации соответствующих функций единичных углов и аргументов. Для усиления пользовательского контроля один вызов
раскладывает все тригонометрические и гиперболические функции от сумм и произведений в комбинации соответствующих функций единичных углов и аргументов. Для усиления пользовательского контроля один вызов  выполняет упрощение на одном уровне. Для управления вычислением имеется флаг
выполняет упрощение на одном уровне. Для управления вычислением имеется флаг  . Изначально флаг
. Изначально флаг  установлен в
установлен в 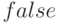 . Если флаг
. Если флаг  установить в
установить в 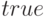 , то функция
, то функция  будет работать до тех пор, пока выражение не перестанет меняться.
будет работать до тех пор, пока выражение не перестанет меняться.
(%i1) x+sin(3*x)/sin(x),trigexpand=true,expand;
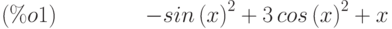
(%i2) trigexpand(sin(10*x+y));
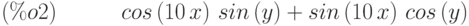
(%i3) trigexpand(sin(3*x)+cos(4*x));

Функция trigreduce свёртывает все произведения тригонометрических и гиперболических функций в комбинации соответствующих функции от сумм. Функция работает не до конца, так что повторный вызов может изменить выражение. При вызове функции в формате trigreduce(expr,x) преобразования осуществляются относительно функций x.
Примеры:
(%i8) trigreduce(cos(x)^4 + cos(x)^3 + cos(x)^2 + cos(x) + 1);
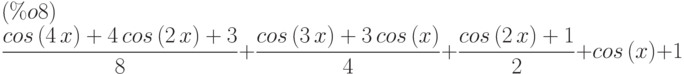
(%i9) trigreduce(-sin(x)^2+3*cos(x)^2+x);
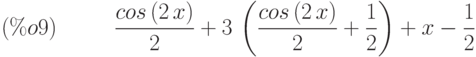
Функция 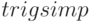 упрощает тригонометрические и и гиперболические выражения, применяя к ним правила
упрощает тригонометрические и и гиперболические выражения, применяя к ним правила 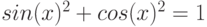 и
и  .
.

(%i1) trigsimp(sin(x)^2+3*cos(x)^2);

(%i2) trigsimp(sinh(x)^2+3*cosh(x)^2);

Функция 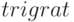 (синтаксис вызова
(синтаксис вызова 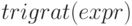 ) приводит заданное тригонометрическое выражение
) приводит заданное тригонометрическое выражение  к канонической упрощённой квазилинейной форме. Это выражение рассматривается как рациональное, содержащее
к канонической упрощённой квазилинейной форме. Это выражение рассматривается как рациональное, содержащее 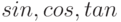 , аргументы которых линейные формы некоторых переменных и
, аргументы которых линейные формы некоторых переменных и 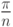 (
( — целое). Всегда, когда возможно, заданное выражение линеаризуется.
— целое). Всегда, когда возможно, заданное выражение линеаризуется.
Пример:
(%i1) trigrat((1+sin(2*b)-cos(2*b))/sin(b));
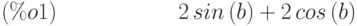
2.7.8 Преобразование степенных и логарифмических выражений
Функция radcan упрощает выражения, содержащие экспоненты, логарифмы и радикалы, путём преобразования к форме, которая является канонической для широкого класса выражений. Переменные в выражении упорядочиваются. Эквивалентные выражения в этом классе не обязательно одинаковы, но их разность упрощается применением radcan до нуля.
Примеры:
(%i1) (log(x+x^2)-log(x))^a/log(1+x)^(a/2);
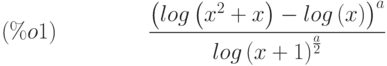
(%i2) radcan(%);

(%i10) (%e^x-1)/(1+%e^(x/2));

(%i11) radcan(%);

Функция 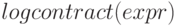 рекурсивно сканирует выражение
рекурсивно сканирует выражение  , преобразуя выражения вида
, преобразуя выражения вида 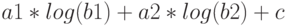 к форме
к форме 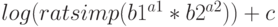 .
.
Пример:
(%i1) 2*(a*log(x)+3*b*log(y));

(%i2) logcontract(%);

Если объявить переменную  целой (используя
целой (используя 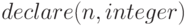 ), функция
), функция 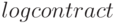 позволяет включить эту переменную в показатель степени:
позволяет включить эту переменную в показатель степени:
(%i1) declare(n,integer);

(%i2) logcontract(3*a*n*log(x));

2.7.9 Пользовательские функции
Для записи функции необходимо указать её название, а затем, в круглых скобках записать через запятую значения аргументов. Если значением аргумента является список, то он заключается в квадратные скобки, а элементы списка также разделяются запятыми.
Пример:
sin(x); integrate(sin(x),x,-5,5); plot2d([sin(x)+3,cos(x)],[x,-%pi,%pi],[y,-5,5]);
Пользователь может задать собственные функции. Для этого сначала указывается название функции, в скобках перечисляются названия аргументов, после знаков := (двоеточие и равно) следует описание функции. После задания пользовательская функция вызывается точно так, как и встроенные функции Maxima.
Пример:
(%i44) f(x):=x^2;

(%i45) f(3 + 7);

Не следует использовать для функций названия, зарезервированные для встроенных функций Maxima. Для создания функций используется также встроенная функция 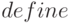 , которая позволяет преобразовать выражение в функцию. Синтаксис вызова
, которая позволяет преобразовать выражение в функцию. Синтаксис вызова 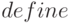 довольно многообразен:
довольно многообразен:
Варианты вызова функции 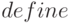 различаются, какой именно объект создаётся: ординарная функция (аргументы в круглых скобках) или массив (аргументы в квадратных скобках). Если первый аргумент — операторы
различаются, какой именно объект создаётся: ординарная функция (аргументы в круглых скобках) или массив (аргументы в квадратных скобках). Если первый аргумент — операторы 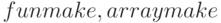 , то функция создаётся и вычисляется (аналогично и ev).
, то функция создаётся и вычисляется (аналогично и ev).
Примеры:
Ординарная функция:
(%i1) expr : cos(y) - sin(x);

(%i2) define (F1 (x, y), expr);
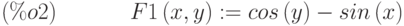
(%i3) factor(F1(a,b));

Создание функции-массива:
(%i1) define (G2 [x, y], x.y - y.x);

Создание массива:
(%i2) define (arraymake (F, [u]), cos(u) + 1);

Использование функции  для задания пользовательской функции:
для задания пользовательской функции:
(%i3) define (ev (foo (x, y)), sin(x) - cos(y));
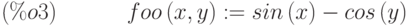


![define(f[x_1,... ,x_n],expr)](/sites/default/files/tex_cache/6de796af93060d58d9407eb3cb665eb1.png)
![define(funmake(f, [x_1,... ,x_n]),expr)](/sites/default/files/tex_cache/ddb9672f6e118b33e3cfceb708f8bcc1.png)
![define(arraymake(f, [x_1,... ,x_n]),expr)](/sites/default/files/tex_cache/f530c7787e1ad339b29b21b9bcf4ee3f.png)
