НОУ ИНТУИТ | Инструктивный синтез нанометровых вычислительных структур. От элементной базы к алгоритмически ориентированным субпроцессорам.. Лекция 5: МКМД-БИТ-потоковые субпроцессоры с (микро)программируемой архитектурой

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 01.10.2013 | Доступ: свободный | Студентов: 260 / 23 | Длительность: 24:58:00

ISBN: 978-5-9963-0223-9

Темы: САПР, Аппаратное обеспечение, Нанотехнологии

Специальности: Разработчик аппаратуры

|

Вам нравится? Нравится 5 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

4.3. Ассоциативные конструкции в базовой системе команд МКМД-бит-потокового (суб)процессора векторно-матричной обработки

В современных задачах цифровой обработки сигналов и изображений темпа реального времени [70] доминируют векторно-матричные преобразования, операционное ядро которых образует скалярное произведение (свертка)

$L(X^{s}_n,Y^s_n)=\sum\limits_{s=1}^{S_n}{X_n^s*Y_n^s}$

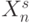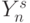двух векторов X_n^s и Y_n^s размерности S_m и разрядности . В результате упрощенная функциональная схема операционного устройства цифровых процессоров обработки сигналов принимает вид рис. 4.6, где все блоки реализованы аппаратно.

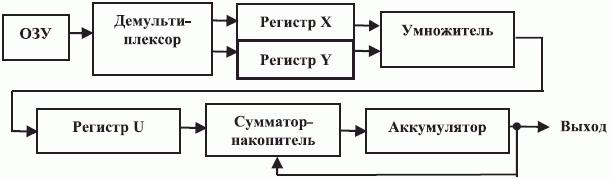
Рис. 4.6. Упрощенная функциональная схема операционного устройства цифровых процессоров обработки сигналов

В векторно-конвейерной арифметике умножение можно выполнить в прямом коде над абсолютными значениями входных векторов $| U^{s}_{2(n-2)}| = |X_{n-2}^s|*| Y_{n-2}^s |$ с последующим присвоением знака $z_u = z_x \oplus z_y$ результату $U^{s}_{2n}$ , где все операнды имеют традиционный для МКМД-бит-потоковой организации вычислений формат фиксированной запятой с "нулевым" старшим разрядом и следующим за ним знаковым разрядом. В этом случае:

$|U^{s}_{2(n-2)}| = \sum\limits_{j=1}^{n-2}{(x_i^s\bigwedge\limits_{i=1}^{n-2}{y_j^s})*2^{j-1}}$

( 4.3)

где $x_i^s\in|X_{n-2}^s|$ , $y_j^s\in|Y_{n-2}^s|$ i,j = \overline{1,n-2} - содержимое бит ( n - 2 )-разрядных модулей множимого $| X^{s}_{n-2}|$ и множителя $| Y^s_{n-2}|.$

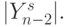
Отвечающая (4.3) схема МКМД-бит-потокового (по $s = (1,\infty)$ конвейерного умножителя (рис. 4.7) работает в соответствии с ассоциативным алгоритмом: для всех $y^{s}_j\in |Y^{s}_{n-2}|:$

$u_{ij}^s(t_0+(s-1)+i+j) = \begin{cases} u_{i}^s(t_0+(s-1)+i+(j-1)) + x_{i}^s(t_0+(s-1)+i+j), & \text{ если } y_{j} = 1, \\ u_{i}^s(t_0+(s-1)+i+(j-1)), & \text{ если } y_{j} = 0. \end{cases}$

( 4.4)

где $u_{ij}^s(t_0+(s-1)+i+j) \in |U_{(n-2)+j}^s(t_0+(s-1)+i+j)|$ , а множитель $2^{j-1}$ реализуется пошаговым наращиванием временного сдвига на (j-1) тактов по отношению к накапливаемой сумме частных произведений.

Здесь: $U_{n-2}^s(t_0+s-1)= const(s) \equiv 0$ , а $t_{0}$ - целочисленное время начальной задержки поступления потоков $| X^{s}_{n-2}|$ и $| Y^{s}_{n-2}|$ на входы умножителя.

Отвечающая (4.4) топологическая схема DD -ассоциативного МКМД-бит-потокового умножителя приведена на рис. 4.7, и в ней:

-й цикл работы продолжительностью тактов задается циклической константой $C_{2n-1}$ вида: первый справа (младший) бит - "единица", а остальные бита - "нули", которая распространяется по каналам транзита первой строки бит-процессоров с задержкой на 2 такта в каждом и передается вниз с задержкой на 1 такт в каждом столбце бит-матрицы;
поток множителей $| Y^{s}_{n}|$ (в каждом из которых 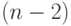младших бита - значащие, а остальные - "нули") распространяется по каналам транзита бит-процессоров 2-й строки (с задержкой на 1 такт в каждом);
содержимое -го бита запоминается циклически (по ) на тактов и с выхода бит-инструкции ST1 передается вниз с задержкой на 2 такта (см. табл. 5.8 курса "Задачи и модели вычислительных наноструктур") в соответствующем -м столбце бит-матрицы;

Рис. 4.7. Топологическая схема микропрограммы DD-ассоциативной слов-инструкции умножения (MLTDD)
поток множимых ? $| X^{s}_{2n}|$ формата: ( ) бит - значащие, а остальные - "нули", распространяется по каналам транзита бит-процессоров 3-й строки с задержкой на 2 такта в каждом и через бит-инструкцию 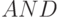ответвляется вниз в каждом столбце бит-матрицы;
операция "сдвиг - сложение" -го множимого с самим собой (в зависимости от содержимого -го бита соответствующего -го множителя) реализуется в бит-процессорах 4-й строки бит-матрицы, причем операция сдвига на 1 разряд в каждом столбце осуществляется за счет дополнительной задержки множимого на 1 такт по отношению к моменту поступления соответствующей суммы частных произведений.

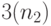В этой схеме время начальной задержки равно ( n-2 ) цикла изменения индекса , а аппаратные затраты на FIFO -регистровую память зависят от линейно: 1-я строка - $2(n _{2})$ бит, 2-я строка - $4(n _{2})$ бит, 3-я строка - $3(n _{2})$ бит, 4-я строка - $2(n _{2})$ бит, что в сумме дает $11(n _{2})$ бит.

Однако скорость приращения индекса равна циклам изменения индекса .

Из приведенных алгоритмов и схем видно, что содержимое бит множителя определяет структуру "сдвигов-сложений", что является необходимой предпосылкой эффективного использования PD -ассоциативных конструкций при построении операционных устройств самого разнообразного функционального назначения.

В схеме конвейерного умножителя рис. 4.7:

регистр является виртуальным и соответствует времени задержки -го бита, множимого на соответствующем входе (первый бит-процессор 3-й строки бит-матрицы);
регистр формируется бит-процессорами 2-й строки бит-матрицы (выходы бит-операций ST1);
регистр также является виртуальным и соответствует времени задержки -го бита произведения на выходе последнего бит-процессора 4-й строки бит-матрицы.

Входящий в состав операционного устройства рис. 4.6 МКМД-бит-потоковый DD -ассоциативный сумматор-накопитель реализуется совместно с аккумулятором (рис. 4.8), и в нем:

входной операнд $U^{s}_{2n}$ имеет разрядность бит, а размерность результирующей матрицы равна элемента;
входной операнд $R_{3m}$ является управляющим, задает период накопления частных произведений и имеет вид циклической константы, в которой бит - "единица", а остальные бит - "нули";
входной операнд $\overline{C^2_{n}1}$ является циклической константой вида: младший бит - "ноль", а остальные 15 бит - "единица", которая используется для обнуления буферных разрядов в 3-х накапливаемых частных суммах.

Рис. 4.8. Топологическая схема DD-ассоциативного сумматора-накопителя для умножения матриц 3*3 (n = 16 бит) (ADDA(DD))

В отличие от обычных алгоритмов поэлементного формирования результирующей матрицы, в МКМД-бит-потоковых субпроцессорах цифровой обработки сигналов используются алгоритмы формирования по строкам или по столбцам, в которых регистр-аккумулятор имеет размерность m*3 , где - соответственно размер результирующей матрицы по числу строк или столбцов. 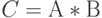В этом случае поточный алгоритм построчного формирования матрицы C = А*В имеет вид:

$a_{11}*<b_{11}, b_{12}, …, b_{1Sm}> \\ +\,\,\,\,\,+\,\,…\,\,+\\ a_{12}*<b_{21}, b_{22}, …, b_{2Sm}> \\ +\,\,\,\,\,+\,\,…\,\,+\\ ……………………\\ a_{1Sm}*<b_{Sm1}, b_{Sm2}, …, b_{SmSm}> \\ =\,\,\,\,\,=\,\,…\,\,=\\ <c_{11}, c_{12}, …, c_{1Sm}>\\ \\ \\ a_{21}*<b_{11}, b_{12}, …, b_{1Sm}> \\ +\,\,\,\,\,+\,\,…\,\,+\\ a_{22}*<b_{21}, b_{22}, …, b_{2Sm}>\\ +\,\,\,\,\,+\,\,…\,\,+\\ …………………… \\ (4.5) a_{2Sm}*<b_{Sm1}, b_{Sm2}, …, b_{SmSm}>\\ =\,\,\,\,\,=\,\,…\,\,=\\ <c_{21}, c_{22}, …, c_{2Sm}>\\ \\ \\ ……………………… \\ \\ \\ a_{Sm1}*<b_{11}, b_{12}, …, b_{1Sm}> \\ +\,\,\,\,\,+\,\,…\,\,+\\ a_{Sm2}*<b_{21}, b_{22}, …, b_{2Sm}> \\ +\,\,\,\,\,+\,\,…\,\,+\\ ........................\\ a_{SmSm}*<b_{Sm1},b_{Sm2}, …, b_{SmSm}> \\ =\,\,\,\,\,=\,\,…\,\,=\\ <c_{Sm1},c_{Sm2}, …, c_{SmSm}>$

В МКМД-бит-потоковых сопроцессорах цифровой обработки сигналов алгоритм (4.5) реализуется следующим образом:

"быстрые" переменные $\{b^{s}_{jk} \}_m$ образуют бит-поток множимых $X^s_m =\{b^{s}_{jk} \}_m$ , в котором индекс изменяется с циклом $m = 2n + lg_2{S_m}$ ; "медленные" переменные $\{a^{s}_{ij}\}_m$ образуют бит-поток множителей $Y^s_n :=\{ a_{ij}^{s} \}_n$ , в котором индекс изменяется с циклом , а каждая $a_{ij}^s$ "хранится" в теле микропрограммы такое же время;
суммирование ведется по столбцам соотношения (4.5), в которых находятся частные произведения $a_{ij}^s * b_{jk}^s$ , причем накопление суммы значения $c^s_{ik}$ осуществляется с помощью одного сумматора с FIFO-регистровым аккумулятором разрядности $S_{m}*m$ .

Одно из главных преимуществ МКМД-бит-потоковых вычислительных технологий - это возможность варьировать разрядностью, а значит, и точностью непосредственно во время вычислений. Достигается это за счет высокой скорости генерацией микропрограмм соответствующих операционных устройств, что обеспечивается очень простыми алгоритмами рекуррентного наращивания микропрограмм, зависящих в данном случае от параметров результирующих потоков данных и .

Действительно, при увеличении разрядности множимого в умножителе (см. рис. 4.7) необходимо соответственно изменить только вид циклической константы $C_{2n}1$ , а при увеличении разрядности множителя умножитель необходимо нарастить соответствующим числом столбцов, которые называются термами. Такой термальный синтез применим и к сумматору-накопителю, в котором варьируемым является только размер аккумулятора, а схемы суммирования и управления периодом накопления остаются неизменными (см. рис. 4.8). В этом случае достаточно использовать ограниченное число термов расширения разрядности аккумулятора и, в частности, терм рис. 4.8-б, если шаг наращивания составляет 18 бит. Этот терм пристраивается справа как столбец бит-матрицы рис. 4.8. Его также можно использовать и при увеличении разрядности данных в слов-инструкции DCC рис. 4.2, которая используется в схеме рис. 4.6 при сопряжении умножителя, работающего в прямом коде, с сумматором-накопителем, работающем в дополнительном коде.

Дальше >>

Авторизоваться

Инструктивный синтез нанометровых вычислительных структур. От элементной базы к алгоритмически ориентированным субпроцессорам.

МКМД-БИТ-потоковые субпроцессоры с (микро)программируемой архитектурой

4.3. Ассоциативные конструкции в базовой системе команд МКМД-бит-потокового (суб)процессора векторно-матричной обработки

Вопросы и ответы