Нейроподобные модели как формально-логический базис анализа живых систем
Разобьем все множество реализуемых ранготроном булевых функций на два класса:
-
задающие, в которых параметр г соответствует номеру базовой позиции линии задержки (
 ), по отношению к которой вычисляется текущее значение
), по отношению к которой вычисляется текущее значение 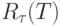 ;
; -
сателлитные, для которых
 .
.
В нашем примере задающие булевы функции те, у которых  :
:
 ;
; 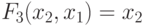 ;
;  , а остальные реализуются как сателлитные.
, а остальные реализуются как сателлитные.
Ослабим требование "цикличности" смещения 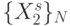 по
по 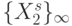 , увеличим размер "скользящего окна"
, увеличим размер "скользящего окна"  и будем считать, что в любой момент времени
и будем считать, что в любой момент времени  оно содержит полный набор входных векторов
оно содержит полный набор входных векторов  , часть из которых повторяется. В этом случае нарушается только монотонный характер изменения лексикографического ранга, но отношение порядка в последовательности рангов остается неизменным и по-прежнему
, часть из которых повторяется. В этом случае нарушается только монотонный характер изменения лексикографического ранга, но отношение порядка в последовательности рангов остается неизменным и по-прежнему  . Повторяемость входных векторов в "скользящем окне" приводит к флуктуациям ранга одного и того же входного вектора на интервале времени
. Повторяемость входных векторов в "скользящем окне" приводит к флуктуациям ранга одного и того же входного вектора на интервале времени  , в результате чего теряется однозначность реализации даже задающей булевой функции:
, в результате чего теряется однозначность реализации даже задающей булевой функции: 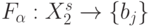 . В таких условиях адаптация порогового вектора в (8.15) позволяет избавиться от неоднозначностей только при реализации задающих булевых функций, а сателлитные булевы функции реализуются в форме стохастического конечного автомата [221].
. В таких условиях адаптация порогового вектора в (8.15) позволяет избавиться от неоднозначностей только при реализации задающих булевых функций, а сателлитные булевы функции реализуются в форме стохастического конечного автомата [221].
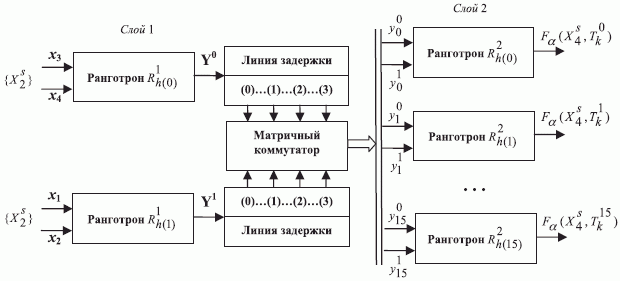
Простейшая ранготронная сеть содержит (рис. 8.9) два слоя двух-входовых булевых ранготронов, объединенных матричным коммутатором, формирующим все парные комбинации выходов двух (внешних) линий задержки. Здесь верхний индекс "внутренней" переменной сети  отражает принадлежность к выходу ранготрона 1-го слоя, а нижний - к выходу линии задержки, по которой эта переменная распространяется по сети.
отражает принадлежность к выходу ранготрона 1-го слоя, а нижний - к выходу линии задержки, по которой эта переменная распространяется по сети.
Время внутренней задержки ( 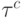 ) будем называть задержкой на формирование выходной реакции
) будем называть задержкой на формирование выходной реакции  -го ранготрона (эквивалент латентного периода реального нейрона), а время внешней задержки (
-го ранготрона (эквивалент латентного периода реального нейрона), а время внешней задержки (  ) - задержкой на распространение реакции
) - задержкой на распространение реакции  -го ранготрона по сети (эквивалент периода рефрактерности аксонно-коллатерных связей реальных нейросетей). В нашем случае матричный коммутатор реализует комбинации
-го ранготрона по сети (эквивалент периода рефрактерности аксонно-коллатерных связей реальных нейросетей). В нашем случае матричный коммутатор реализует комбинации  задержек распространения, формируя значения входных векторов для ранготронов второго слоя сети в соответствии с матрицей
задержек распространения, формируя значения входных векторов для ранготронов второго слоя сети в соответствии с матрицей  (табл. 8.7).
(табл. 8.7).
 |
 |
 |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
0 | 1 | 2 | 3 |  |
0 | 1 | 2 | 3 |  |
0 | 1 | 2 | 3 |
| 0 | (0,0) | (0,1) | (0,2) | (0,3) | 0 |  |
 |
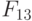 |
 |
0 |  |
 |
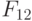 |
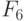 |
| 1 | (1,0) | (1,1) | (1,2) | (1,3) | 1 |  |
 |
 |
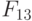 |
1 | 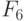 |
 |
 |
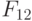 |
| 2 | (2,0) | (2,1) | (2,2) | (2,3) | 2 | 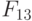 |
 |
 |
 |
2 | 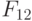 |
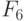 |
 |
 |
| 3 | (3,0) | (3,1) | (3,2) | (3,3) | 3 |  |
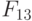 |
 |
 |
3 |  |
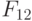 |
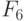 |
 |
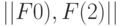 | ||||||||||||||
 |
0 | 1 | 2 | 3 | ||||||||||
| 0 |  |
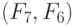 |
 |
 |
||||||||||
| 1 |  |
 |
 |
 |
||||||||||
| 2 |  |
 |
 |
 |
||||||||||
| 3 |  |
 |
 |
 |
||||||||||
Базовая задержка 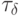 влияет на работу ранготрона и всей ранго-тронной сети следующим образом. Зафиксируем
влияет на работу ранготрона и всей ранго-тронной сети следующим образом. Зафиксируем  . Тогда в соответствии с (8.14) матрица
. Тогда в соответствии с (8.14) матрица  порождает последовательность
порождает последовательность  ;
;  ;
; 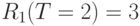 ;
;  и так далее в цикле начиная с
и так далее в цикле начиная с  .
.
В этом случае согласно (8.16) ранготрон реализует булевы функции:
Повторив эту процедуру для  и
и  , получим матрицу
, получим матрицу 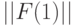 (см. табл. 8.7) циклических сдвигов булевых функций, реализуемых ранготроном. В этой матрице главная диагональ по определению образована задающей булевой функции (
(см. табл. 8.7) циклических сдвигов булевых функций, реализуемых ранготроном. В этой матрице главная диагональ по определению образована задающей булевой функции (  ), а сателлитные булевы функции циклически смещаются в зависимости от значения базовой задержки. Проделав аналогичную процедуру для системы решающих правил (8.17), получим матрицу
), а сателлитные булевы функции циклически смещаются в зависимости от значения базовой задержки. Проделав аналогичную процедуру для системы решающих правил (8.17), получим матрицу  (см. табл. 8.7).
(см. табл. 8.7).
Пусть нулевой ранготрон первого слоя сети рис. 8.9 работает согласно  , реализуя
, реализуя 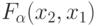 , а первый ранготрон этого же слоя работает согласно
, а первый ранготрон этого же слоя работает согласно  , реализуя
, реализуя  . Тогда при фиксированных
. Тогда при фиксированных  и варьируемых значениях
и варьируемых значениях  образуется матрица комбинаций
образуется матрица комбинаций  булевых функций (см. табл. 8.7), а смещение базы
булевых функций (см. табл. 8.7), а смещение базы 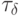 в линии внутренней задержки ранготрона обеспечивает временную (в данном случае циклическую) перестановку реализуемых им булевых функций. Здесь верхний индекс связан с номером ранготрона в соответствующем слое сети. Независимая вариация смещений
в линии внутренней задержки ранготрона обеспечивает временную (в данном случае циклическую) перестановку реализуемых им булевых функций. Здесь верхний индекс связан с номером ранготрона в соответствующем слое сети. Независимая вариация смещений 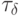 у ранготронов предыдущего слоя сети обеспечивает формирование различных пар "внутренних" переменных на входах ранготронов последующего слоя сети, так как матричный коммутатор создает все пары
у ранготронов предыдущего слоя сети обеспечивает формирование различных пар "внутренних" переменных на входах ранготронов последующего слоя сети, так как матричный коммутатор создает все пары  , для которых определены матрицы типа
, для которых определены матрицы типа  .
.
Можно убедиться [252], что вариации  перемещают задающую булеву функцию всей сети
перемещают задающую булеву функцию всей сети 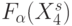 на любой ее выход, так как организованная по принципу "каждый с каждым" ранготронная сеть носит пространственно-временной характер.
на любой ее выход, так как организованная по принципу "каждый с каждым" ранготронная сеть носит пространственно-временной характер.
Ранготронная сеть может работать и в асинхронном режиме [252], что ослабляет требование принадлежности (в любой момент времени  полного набора входных векторов
полного набора входных векторов  "скользящему окну"
"скользящему окну"  . В этом случае вычисление ранга
. В этом случае вычисление ранга  необходимо продолжать до тех пор, пока через ранготрон не пройдет полный набор
необходимо продолжать до тех пор, пока через ранготрон не пройдет полный набор  . Поэтому в асинхронном ранготроне появляется нестабильный латентный период, который определяется варьируемым временем накопления ранга.
. Поэтому в асинхронном ранготроне появляется нестабильный латентный период, который определяется варьируемым временем накопления ранга.
Отсюда, отсутствие у существующих моделей функционально значимого латентного периода и периода рефрактерности исключает фактор влияния внутренней активности отдельных нейронов на физиологически важную функцию пространственно-временной интеграции входных возмущений во всей нейросети [25].
В пределах одного поведенческого акта морфология реальной нейросети достаточно стабильна, а сама сеть, вообще говоря, не ориентирована направлении от определенного (под)множества входов 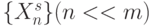 к какому-то определенному набору
к какому-то определенному набору  -выходов. В таких условиях зависимость пространственно-временного положения булевой функции от соотношений
-выходов. В таких условиях зависимость пространственно-временного положения булевой функции от соотношений  является важным фактором управления нейрональной сетью, в которой активность каждого нейрона проявляется в том, что адекватная входному воздействию
является важным фактором управления нейрональной сетью, в которой активность каждого нейрона проявляется в том, что адекватная входному воздействию  реакция нейросети существенно зависит от выбора в каждом из них базовой позиции во входной последовательности. При этом выбор
реакция нейросети существенно зависит от выбора в каждом из них базовой позиции во входной последовательности. При этом выбор 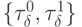 определяется не только внешними, но и внутренними факторами, требующими скоординированной субней-рональной активности по
крайней мере подмножества нейронов сети, обеспечивающих отображение
определяется не только внешними, но и внутренними факторами, требующими скоординированной субней-рональной активности по
крайней мере подмножества нейронов сети, обеспечивающих отображение 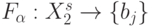 .
.
Из приведенных данных также следует, что принятая у современных исследователей оценка эффективности работы нейрокомпьютера измеряется количеством коммутаций/c [170, 255], но она имеет мало общего с реальными нейросетями, где эффект групповой (пере)коммутации промежуточных переменных играет более важную роль, чем частные пересылки данных, так как такой эффект является одним из существенных механизмов синтеза целенаправленных поведенческих актов, направленных на удовлетворение доминирующей мотивации [25, 249].
Таким образом, ранготрон и сети на его основе:
- Позволяют исследовать механизмы, более адекватные по своим мор-фофункциональным свойствам реальным нейронам и нейронным ансамблям, чем предшествующие модели формальных нейронов.
- Существенно используют входную неоднозначность, связанную с временем задержки на формирование и распространение промежуточных переменных сети. В результате ранготронная сеть обладает качественно новым свойством группового управления пространственно-временным положением выходных реакций неориентированной нейросети.
- Являются статистически неустойчивыми в том смысле, что на их выходах могут присутствовать сателлитные булевы функции с явно стохастическим характером отображения
 для разных значений
для разных значений  . Поэтому настройка ранготронной сети состоит в том, чтобы скоординированно по времени и пространству получить на ряде "биологически важных" выходов сети спектр задающих булевых функций, определенных на произвольных подмножествах
. Поэтому настройка ранготронной сети состоит в том, чтобы скоординированно по времени и пространству получить на ряде "биологически важных" выходов сети спектр задающих булевых функций, определенных на произвольных подмножествах  из
из  , где
, где  .
. - Неиспользуемые в традиционных моделях факторы задержки на формирование выходной реакции нейрона и на ее распространение по нейросети создают качественно новые возможности и для распараллеливания вычислений за счет одновременного соотнесения реакции выхода произвольному вектору, поступившему на вход за время задержки, и для управления сетью нейроподобных элементов.
При этом следует помнить, что варьируемое время задержки в ранготроне и ранготронной сети отражает не саму избирательную биологическую или физиологическую активность, а только ее интегральные последствия.
" Нечисленная " идентификация и голографический принцип системной организации процессов жизнедеятельности. Биологические процессы соподчинены законам физики, по которым функционируют эволюцион-но более ранние нелинейные неравновесные системы. Поэтому управление несколькими тысячами сопряженных химических реакций с множеством глубоких обратных связей, поддерживающих метаболизм только одной клетки, представляет собой задачу, практически неразрешимую строгими формальными методами. В таких условиях полуэмпирическую схему инструктированного синтеза на основе формально-логической конструкции "если…, то…" можно считать уникальной возможностью повышения сложности биологических систем без потери их управляемости. Основные достоинства такой схемы инструктированного синтеза макромолекул нативных белков:
- она поддерживает найденное эмпирическим путем корректное сопряжение фиксированной совокупности нелинейных и неравновесных химических реакций, которое можно осуществить при фиксированном комплексе метастабильных внешних условий; при этом поиск и отбор самих нелинейных и неравновесных химических реакций производится флуктуационными методами и средствами формирования диссипативных структур;
- она позволяет без потери информативности включать химические реакции-предшественники в качестве самостоятельных единиц, сопрягаемых химическими реакциями-наследниками, что воспринимается и как иерархия управления биологическими объектами возрастающей сложности, и как иерархия организации памяти живых систем.
Требование сохранности информации, заложенной в субстрат нижнего уровня иерархии, можно удовлетворить, если перейти к структурно-параметрическим методам и средствам хранения и преобразования информации [256]. В этом случае память представляет собой структурно-функциональное образование ассоциативного типа, которое не только хранит, но и преобразует информацию, что согласуется с голографическим принципом системной организации процессов жизнедеятельности К.В. Судакова [250]. Согласно этому принципу, потребность выступает в качестве опорной волны, которая формируется на основе доминирующей мотивации и выступает в качестве акцептора результатов действия, по П.К. Анохину [25]. Предметная волна по аналогии с физической голограммой формируется под воздействием результатов поведенческого акта и интерферирует с опорной волной на разных уровнях иерархии [ 250]:
- на клеточном уровне под воздействием сигналов о потребности происходит экспрессия эффекторных специфических белков, которые управляют ростом, дифференцировкой клеток и их метаболизмом, направленным на опережающее устранение возникшей потребности;
- на межклеточном уровне многочисленные биологически активные вещества (белковые молекулы, гормоны, олигопептиды и так далее) взаимодействуют с мембранами клеток, образуя второй уровень голографического экрана;
- на уровне структур мозга голографический экран поддерживается взаимодействием коллоидов глии с молекулами ДНК и РНК отдельных нейронов.
Из приведенных данных следует, что между физической голографией с одной стороны и молекулярно-биологической и физиологической голографией с другой стороны имеется принципиальное отличие. В физических голограммах информация кодируется параметрами сигналов, а в молекулярно-биологических голограммах информационные процессы на всех уровнях иерархии организма и его нервной системы поддерживаются структурно-параметрическими методами и средствами, которые невозможно осуществить без инструктированного синтеза субстратов, участвующих в метаболизме клеток и нейронов.
Это отличие приводит к тому, что расширение емкости физической голографической памяти за счет ее иерархической организации достигается только при определенных ограничениях на допустимую структуру связей нижнего уровня. В частности, в оптических вычислителях на произвольно коммутируемых через голографическую память вентильных матрицах [228] отличают пространственно-переменные и пространственно-инвариантные (однородные) связи. Чтобы обеспечить произвольный доступ к каждому из  вентилей матрицы в первом случае требуется база, пропорциональная
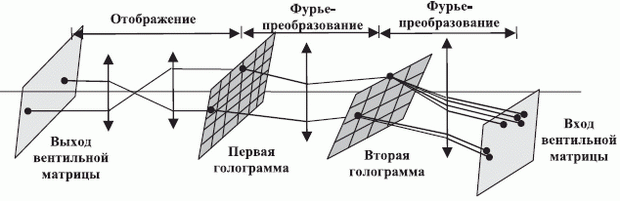
вентилей матрицы в первом случае требуется база, пропорциональная  . Под базой понимается произведение пространственной протяженности оптического вентиля на ширину полосы частот реализуемого Фурье-преобразования (рис. 8.10).
. Под базой понимается произведение пространственной протяженности оптического вентиля на ширину полосы частот реализуемого Фурье-преобразования (рис. 8.10).
Из-за ограничений устройств записи база голограммы в тот период времени позволяла управлять произвольной коммутацией между 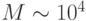 оптическими вентилями. При пространственно-инвариантной организации связей схема соединения
оптическими вентилями. При пространственно-инвариантной организации связей схема соединения  вентилей фиксирована и поэтому база пропорциональна
вентилей фиксирована и поэтому база пропорциональна  , что позволяло создавать голографически управляемые матрицы из
, что позволяло создавать голографически управляемые матрицы из  оптических вентилей. Отсюда, поднять на 4 порядка информационную емкость физической голограммы удалось только за счет перехода к однотипным структурам связей, что резко ограничило выбор возможных архитектур оптических процессоров. Поэтому в качестве компромисса была предложена гибридная схема организации голографической памяти (см. рис. 8.10), в которой на нижнем уровне иерархии пространственно-инвариантные связи поддерживались между
оптических вентилей. Отсюда, поднять на 4 порядка информационную емкость физической голограммы удалось только за счет перехода к однотипным структурам связей, что резко ограничило выбор возможных архитектур оптических процессоров. Поэтому в качестве компромисса была предложена гибридная схема организации голографической памяти (см. рис. 8.10), в которой на нижнем уровне иерархии пространственно-инвариантные связи поддерживались между  вентилями,
образующими ячейки с пространственно-переменными связями между собой. В совокупности это позволило довести размер управляемой матрицы до
вентилями,
образующими ячейки с пространственно-переменными связями между собой. В совокупности это позволило довести размер управляемой матрицы до 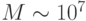 оптических вентилей.
оптических вентилей.
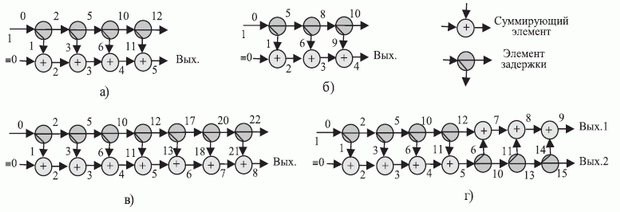
При структурно-параметрической организации памяти иерархия позволяет практически неограниченно наращивать ее емкость с сохранением информативности. Этот эффект достигается за счет того, что на каждом уровне иерархии принадлежащий ему молекулярно-биологический субстрат можно рассматривать как независимый носитель структурно закодированной информации. В частности, исходный, абстрактный молекулярный субстрат рисунок6 при подаче на их входы одиночного возбуждающего импульса воспроизводит на выходах двоичные последовательности вида: 10001011 (рис. 8.11-а) и 01010001 (рис. 8.11-б).
Эти последовательности можно интерпретировать как целые числа 139 и 81, если считать, что младший значащий разряд расположен справа и появляется на выходе с задержкой на 5 и 4 такта соответственно. В вычислительной технике симметричное, последовательное соединение исходного "субстрата" синтезирует "продукт" (рис. 8.11-в), который реализует преобразование  , порождающее с 8 такта последовательность вида
, порождающее с 8 такта последовательность вида  .
.
В реальном метаболизме последовательное соединение исходного субстрата не может произойти без изменений их пространственной структуры, что приведет к формированию новой двоичной последовательности. В частности, при асимметричном соединении исходного субстрата (рис. 8.11-г) синтезированный "продукт" реализует преобразование  , которому на верхнем выходе соответствует двоичная последовательность вида
, которому на верхнем выходе соответствует двоичная последовательность вида 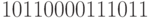 (начиная с 9 такта). При этом в асимметричной структуре можно сохранить в неизменном виде только множимое, то есть операнд 139, который появится на нижнем выходе начиная с 15 такта.
(начиная с 9 такта). При этом в асимметричной структуре можно сохранить в неизменном виде только множимое, то есть операнд 139, который появится на нижнем выходе начиная с 15 такта.
Отсюда, в реальных условиях для воспроизводства информации, структурно представленной в исходном субстрате, необходима деструкция продукта, соразмерная с условиями его синтеза, что предполагает
глобальную обратимость метаболических процессов нейронов. При этом следует учитывать [256], что реакция структурно организованной памяти зависит от возбуждающего сигнала, который может быть и не единичным, а интерпретация выходной двоичной последовательности, как и у ранготрона, зависит от начальной задержки. В частности, если интерпретировать результаты возбуждения одиночным импульсом исходного субстрата не с 5 и 4 тактов, а с 4 и 3 соответственно, то выходные последовательности примут вид  (рис. 8.11-а) и
(рис. 8.11-а) и  (рис. 8.11-б), что соответствует числам
(рис. 8.11-б), что соответствует числам  и
и  . Поэтому в живых системах должны быть механизмы, устраняющие или ослабляющие подобного рода неоднозначные
реакции памяти, что и создает предпосылки для активного восприятия и отображения организмом конкретных внешних и внутренних событий.
. Поэтому в живых системах должны быть механизмы, устраняющие или ослабляющие подобного рода неоднозначные
реакции памяти, что и создает предпосылки для активного восприятия и отображения организмом конкретных внешних и внутренних событий.
Информационный базис "нечисленной" идентификации связан с алгоритмической теорией измерений А.П. Стахова [37], в рамках которой проводится принципиальное различие между шенновской и измерительной неопределенностью. Первая характеризует неопределенность отбора измеряемой величины из множества возможных, что типично для условий подготовки эксперимента. Вторая характеризует незнание "индивидуального" значения величины, уже отобранной для измерения. Неопределенность первого типа можно оценить комбинаторной мерой количества информации [51]  , с помощью которой достаточно просто определяется количество бит, необходимых для передачи и хранения известного сообщения. В нашем случае знание количества бит позволяет выбирать систему "гирь", покрывающую нужды "нечисленной" идентификации, проводимой с помощью рычажных весов.
Здесь считается, что идентифицируемый объект
, с помощью которой достаточно просто определяется количество бит, необходимых для передачи и хранения известного сообщения. В нашем случае знание количества бит позволяет выбирать систему "гирь", покрывающую нужды "нечисленной" идентификации, проводимой с помощью рычажных весов.
Здесь считается, что идентифицируемый объект  принадлежит конечному множеству
принадлежит конечному множеству 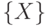 из
из  неповторяющихся элементов, и поэтому "информационная энтропия" выбора объекта
неповторяющихся элементов, и поэтому "информационная энтропия" выбора объекта  равна
равна 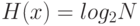 . Отсюда, выбрав конкретный объект идентификации
. Отсюда, выбрав конкретный объект идентификации 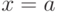 , мы снимаем эту неопределенность, то есть сообщаем "информацию"
, мы снимаем эту неопределенность, то есть сообщаем "информацию"  . На втором этапе производится снятие "индивидуальной" неопределенности, которое состоит в заполнении I бит "нулями" и "единицами" в зависимости от результатов многошаговой процедуры сравнения, которая является детерминированной и состоит в последовательных замещениях более "тяжелых гирь" суммой более "легких гирь", если чаша с "гирями" перетягивает чашу с идентифицируемым объектом [37]. В итоге формируется индивидуальный
. На втором этапе производится снятие "индивидуальной" неопределенности, которое состоит в заполнении I бит "нулями" и "единицами" в зависимости от результатов многошаговой процедуры сравнения, которая является детерминированной и состоит в последовательных замещениях более "тяжелых гирь" суммой более "легких гирь", если чаша с "гирями" перетягивает чашу с идентифицируемым объектом [37]. В итоге формируется индивидуальный  -битный код однозначно идентифицированного объекта.
-битный код однозначно идентифицированного объекта.
" Нечисленная " идентификация и " системоквант " поведения. Принцип опережающего отражения действительности П.К. Анохина [25] лежит в основе приспособительной деятельности организма к повторяющимся событиям внешней среды, которые образуют пространственно-временной
континуум. При этом активность организма в обучении вообще и в выработке условных рефлексов в частности как раз и состоит в событийной дискретизации непрерывного потока и в установлении в нем достаточно условных "причинно-следственных" связей, которые обеспечивают опережающий запуск биологических и физиологических механизмов и гарантируют тем самым достижение полезного приспособительного эффекта. Именно гипербольшое количество альтернатив, обеспечивающих однозначный, но не взаимно однозначный переход от непрерывного к дискретному пространственно-временному потоку событий, создает необходимые условия активного взаимодействия живых систем с окружающей средой. Такой неоднозначный переход в пределе граничит с волюнтаризмом, но тем не менее, он предопределяет гипербольшое многообразие форм приспособительной деятельности различных организмов и даже особей в одних и тех же внешних условиях.
В технике дискретизацию непрерывных во времени процессов осуществляют согласно теореме Котельникова 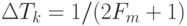 , которая связывает период равномерной дискретизации
, которая связывает период равномерной дискретизации  с максимальной частотой гармонических колебаний
с максимальной частотой гармонических колебаний 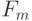 в спектре преобразуемого сигнала, что гарантирует взаимно однозначный переход от непрерывного к дискретному.
в спектре преобразуемого сигнала, что гарантирует взаимно однозначный переход от непрерывного к дискретному.
В живых системах цель дискретизации совершенно иная и состоит в нахождении баланса между нелинейными авторегуляторными (автокаталитическими) механизмами самоорганизации и механизмами инструктированного синтеза и управления. На физиологическом уровне нелинейные авторегуляторные механизмы предполагают наличие функциональных систем, поддерживающих их устойчивость. Поэтому "системоквант" [25] физиологического поведения не может быть постоянным во времени, так как должен обладать атрибутами целостного поведенческого акта, выраженными "языком" соответствующего уровня самоорганизации. Сопряжение "системоквантов" более низкого уровня иерархии в организме и в его нервной системе можно осуществить с помощью более простых механизмов "нечисленной" идентификации, запускающих цепочку "системоквантов", которые и формируют поведенческий акт более высокого уровня иерархии.