Нейроподобные модели как формально-логический базис анализа живых систем

Изначально физики исходили из того, что предоставленная самой себе физико-химическая система всегда придет к "статистическому идеалу" в виде равновесного состояния, для которого характерна полная неупорядоченность (неразличимость) на молекулярном уровне. Однако это справедливо только для изолированных систем, которые не способны обмениваться массой и энергией с внешней средой. Согласно Больцману, энтропия таких систем возрастает до максимального значения, характерного для термодинамического равновесия, так как 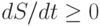. Именно по этой причине упорядоченность в физике стали связывать со снижением энтропии, но приведенное неравенство исключает возможность даже спонтанного образования упорядоченных структур в изолированных системах.

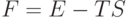Замкнутые системы способны обмениваться энергией с внешней средой, и при фиксированной температуре их поведение уже определяется не столько энтропией, сколько свободной энергией Гельмгольца [33]: , которая стремится к минимуму при приближении системы к равновесному состоянию. Здесь - внутренняя энергия замкнутой системы. Вероятность обнаружить замкнутую систему в равновесном состоянии с энергией 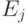определяется соотношением Ландау - Лившица [248]: 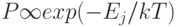, из которого следует, что при достаточно низких температурах заселенными могут быть только уровни с малыми значениями 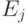, что говорит о наличии элементарной упорядоченности. (Здесь - постоянная Больцмана.) Но с ростом вклад энтропии в энергию Гельмгольца становится сравнимым с внутренней энергией замкнутой системы 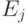, что и приводит к выравниванию заселенности различных энергетических уровней, то есть к росту энтропии и разрушению элементарного порядка. Отсюда, при низких температурах в неизолированных системах возможно образование низкоэнтропийных, равновесных (больцмановских) упорядоченных структур, что и наблюдается в процессах низкотемпературной кристаллизации.

Приведенные данные говорят о том, что больцмановского механизма упорядочения явно недостаточно, чтобы при комнатных температурах образовался "сгусток материи" в виде полимера белка, молекулярный вес которого находится на уровне 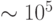, в то время как у воды он составляет всего 18. Однако биологические системы являются не замкнутыми, а (полу) открытыми, то есть они способны (избирательно) обмениваться с внешней средой не только энергией, но и массой. Поэтому для описания открытых систем потребовался расширенный вариант второго закона термодинамики [33], который учитывает изменение энтропии 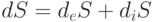за время 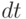как за счет потока энтропии (d S), так и за счет ее производства ( 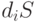) внутри системы. Первая составляющая энтропии обусловлена обменом массой и энергией с внешней средой, а вторая - необратимыми процессами внутри системы (диффузия, теплопроводность, химические реакции и т. п.).

Отсюда, открытые системы отличаются от изолированных систем наличием потока энтропии, соответствующего обмену массой и/или энергией с внешней средой. Но если производство энтропии всегда положительно, то поток энтропии может иметь произвольный знак, что позволяет открытой системе (при 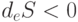) переходить в состояния с более низкой энтропией. С точки зрения соотношения Ландау - Лившица такой переход маловероятен, но само состояние может существовать как угодно долго при выполнении в системе условий стационарности, когда 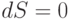, но 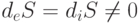. Неравенство нулю потока и производства энтропии является необходимым условием образования диссипативных структур, и для его поддержания требуется достаточно большой поток отрицательной энтропии, который поступает в систему бесконечно долго и сохраняет в ней некоторую упорядоченность. Именно поддержание неравновесных условий препятствует выполнению "р авновесного" равенства 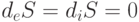. Таким образом, главным источником диссипативной упорядоченности являются устойчивые когерентные флуктуации, стабилизированные обменом массой и/или энергией с внешней средой, которая поддерживает неравновесные условия в системе.

Вместе с тем механизмы диссипативного упорядочения оказались достаточными только на предбиологическом этапе эволюции, когда зародились относительно сложные макромолекулы, способные вступать в автокаталитические реакции [34]. При этом для поддержания самовоспроизводства таких макромолекул предбиологические системы должны были стремиться к состояниям, максимально устойчивым к ошибкам (флуктуациям) копирования, которые свойственны веществам, обладающими определенными автокаталитическими свойствами. Качественный скачок в эволюции биологических систем, согласно М. Эйгену наступил после того, как были освоены механизмы инструктированного синтеза макромолекул белка, многопороговая модель которых показала (см. раздел 8.2):

• в процессе инструктированного синтеза нативных белков используется вариационный механизм структурно-параметрической идентификации, положительный результат которой запускает спусковой механизм отделения аминокислоты от аминоацилового комплекса и включение ее в состав синтезируемого полимера белка;
• неравенство 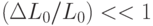говорит о флуктуационном характере взаимной идентификации кодонов и антикодонов, что характерно для диссипативных структур.

Переход к инструктированному синтезу биологических макромолекул не изменил базовые механизмы самоорганизации диссипативных структур, в которых используются количественные соотношения непрерывного типа, через которые выражаются физико-химические законы, обуславливающие взаимодействие исходных компонентов, объединяемых в пространственные структуры. Но организация диссипативных структур напрямую зависит от переноса энергии с микро- на макроуровень открытых неравновесных систем, в то время как в инструктированном синтезе биологических макромолекул количественные соотношения используются только в процессе взаимной идентификации информационных и транспортных рибонуклеиновых кислот, а подстановка соответствующих аминокислот в пространственную структуру синтезируемого белка осуществляется с вероятностью "единица", если произошло взаимное узнавание кодона -РНК и (квази)комплементарного ему антикодона -РНК.

Проведенная в 8.2 формализация позволила численно выразить и отношение вырожденности, и отношение комплементарности в биологическом коде, а проверить само отношение комплементарности можно не только численными, но и "нечисленными" методами и средствами. В последнем случае условие (8.6) можно проконтролировать парным сравнением 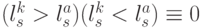, результат которого представляет собой логическое противоречие, связанное с одновременным выполнением двух взаимоисключающих неравенств, что в конечном счете интерпретируется как численное равенство. Здесь - логическое произведение (И). В этом случае уже не требуется точное знание численных значений 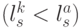, а процедуру сравнения идентификационных активностей кодонов и антикодонов можно реализовать с помощью "биологических рычажных весов".

В итоге оператор линейной свертки 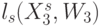, отражающий взвешенную идентификационную активность нуклеотидов, можно заменить группой подстановок (см. раздел 4.7 [100]): , которая при 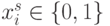представляет собой прямое произведение групп подстановок индексов , где:

• группа инверсии знаков компонент весового вектора (при неизменных абсолютных значениях) индуцирует изоморфную группу подстановок 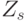значений свертки 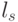компонент весового вектора, а с ними и индексов на скалярной оси ;
• группа подстановок (по индексу ) множества компонент весового вектора над компонентами входного вектора (порядок групп !) изменяет порядок расположения весовых коэффициентов в (8.1) над входными переменными 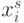, что индуцирует изоморфную группу подстановок 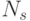значений свертки 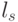, а вместе с ними и индексов на скалярной оси ,
• оператор ассоциативного суммирования 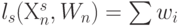- компонент весового вектора порождает систему неоднозначных неравенств , которые и индуцируют группу подстановок .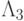

Переход к группе подстановок, порождаемых оператором взвешенного суммирования идентификационных активностей нуклеотидов, не нарушает общности модели, так как, согласно теореме Кэли [103], любую конечную группу (преобразований) можно представить группой подстановок.

Таким образом, в процессе эволюции реализована схема типа "если…, то…", в которой запуск спускового механизма отрыва мономера белка от аминоацилового комплекса и включения его в состав полимера белка можно осуществить "нечисленным" сравнением. Эта схема только впоследствии была взята на вооружение кибернетиками, но с использованием численных соотношений. Более того, "нечисленные" сравнения по своей сути первичны, так как в окружающем нас мире равенство можно считать абстракцией, что подтверждено иррациональным характером всех фундаментальных физических и химических констант.

Проведенный анализ источников возникновения неоднозначностей в природе показал:

1. Неоднозначная идентификация физико-химических объектов, от которой невозможно избавиться даже с привлечением фундаментальных констант:
   • предопределяет необходимость использования полуэмпирических методов и средств управления сложным нелинейным комплексом молекулярно-биологических процессов с глубокими обратными связями;
   • служит главным источником имитационного моделирования, которое обеспечивает любому организму необходимые условия восприятия и последующего анализа всех внешних воздействий.
2. Механизмы структурно-параметрической идентификации кодонов и антикодонов, через которые реализуется инструктированный синтез полимеров нативного белка, не исключают, а только дополняют механизмы формирования диссипативных структур. Такое соотношение между механизмами-наследниками и механизмами-предшественниками можно считать атрибутом всех этапов и уровней сложности эволюции. Этот атрибут проявляется в том, что механизмы инструктированного синтеза нативных белков и предбиологические механизмы диссипативного упорядочения продолжают сосуществовать и эффективно использоваться и на морфофункциональном, и на физиологическом уровне организации живых систем в форме регуляторных процессов субклеточного и клеточного уровней, дифференцировки тканей, условных рефлексов и т. д.

8.6. "Нечисленная" идентификация как средство повышения сложности живых систем

В живых системах однажды освоенные механизмы управления сохраняются по мере нарастания их структурно-функциональной сложности, что, в частности, характерно для физиологических механизмов, лежащих в основе мотивации [249], опережающего отражения повторяющихся событий внешнего мира [25], голографического принципа работы мозга [250] и т. д. В справедливости данного утверждения проще всего убедиться, сравнив схему инструктированного синтеза биополимеров с классической схемой условного рефлекса, в которой условный стимул функционально эквивалентен процедуре взаимной идентификации кодонов и антикодо-нов, которая запускает механизмы отрыва мономера белка от аминоаци-лового комплекса и подстановки его в полимер синтезируемого белка.

С формальных позиций такую схему можно представить конструкцией "если…, то…", в которой причина и следствие имеют разную физико-химическую, молекулярно-биологическую или физиологическую природу, а сама причинно-следственная связь устанавливается эмпирическим путем. Главные достоинства такой формальной конструкции:

• она сохраняет многоальтернативность исходов сравнения и вытекающих из них следствий, что является необходимым условием активного отношения живого к окружающей среде;
• она позволяет устанавливать искусственные (условные, а в ряде случаев и волюнтаристские) причинно-следственные связи между предметами и процессами разной модальности и с разными энергетическими или информационными последствиями, реализуемыми в фиксированном комплексе внешних условий и только в нем.

Покажем роль формально-логической конструкции "если…, то…" (альтернативного следования) в нейрокибернетических системах, где информационная составляющая "если…" формируется методами и средствами нечисленной идентификации, а следствие "то…" представляет собой управление другим информационным или энергетическим процессом, инструктированным синтезом субнейрональных или межнейрональных структур и т. п.

Мотивация и "нечисленные" стохастические модели формальных нейронов. В современной (нейро)кибернетике сложилась ситуация, аналогичная той, которая предопределила развитие методов и средств статистической физики и нелинейной термодинамики. Современные (нейро)математики [70, 87, 88] только нащупывают эффективные пути управления системами из сверх- и гипербольшого количества детерминированных дискретных элементов, взаимосвязи и функции которых постоянно меняются. В частности, даже возродившие интерес к нейроматематике и нейрокомпью-терным технологиям сети Хопфилда - Танка учитывают только электрофизиологическую активность реальных нейронов и обучаются методами и средствами равновесной термодинамики, что явно не адекватно условиям функционирования реальных нейросетей.

Для физиологов и (нейро)математиков первоочередной интерес представляет поиск прямых методов и средств измерения величины мотиваци-онного потенциала, который не только задает направление приложения биологической и физиологической активности, но и существенно ограничивает гипербольшое количество возможных альтернативных путей достижения полезного приспособительного эффекта. Такая роль мотивации во всей архитектуре поведенческого акта указывает на то, что величина мотивационного потенциала характеризует интегральную степень "(полу) открытости" всего организма, а тип этого возбуждения (голод, жажда и т. п.) характеризует направление этой "(полу)открытости". Как было показано выше, в точных науках такие величины задаются градиентами отдельных ингредиентов. В физиологии это сделать не удается, и поэтому мотивацию измеряют косвенными методами: либо сроком депривации, косвенно характеризующим степень истощения резервов организма, либо количеством потребления того или и ного ресурса, восполняющего исходный дефицит, либо величиной преодолеваемого препятствия на пути к удовлетворению мотивации и т. п. Модальность мотивации (направление (полу)открытости) определяется по качеству подкрепления, предпочтенного в условиях выбора, что можно сделать только апостериори.

Но одной "(полу)открытости" какой-либо части клеток явно недостаточно, чтобы организм направил свою деятельность на "замыкание" по этим ингредиентам, так как в живых системах потребность - это особая форма отношений живого к окружающей среде, выражающая необходимость его избирательного взаимодействия с некоторыми элементами этой среды для пластичного, энергетического и информационного обеспечения собственной потребности [251]. Поэтому раскрытые К.В. Судаковым [249] системные механизмы мотивации обуславливают изменение отношения организма с внешней средой, что не может не вызывать в нем переходный процесс от одной внутренней упорядоченности (в том числе и диссипатив-ной) к другой. При этом с "тоническими" показателями мотивации обычно связывают готовность организма к реализации той или иной функции, в то время как широко используемая в формальных моделях нейронов "спай-кова я" активность совпадает с самой реализацией требуемой функции. Это указывает на то, что "спайковая" активность подходит не только для преобразования информации, но и для единовременного оперативного управления структурно-функциональной схемой нейрональной подсети, когда имеются альтернативные возможности функционирования, зависящие от содержимого обрабатываемой информации (ассоциативное управление).

Такое соотношение между "тонической" и "спайковой" активностью можно продемонстрировать с помощью ранготронной модели [252], в основе которой лежит "нечисленное" сравнение и вычисление целочисленного ранга текущего входного вектора в постоянно обновляемой конечной упорядоченной последовательности входных векторов. Вычисление ранга уже само по себе требует учета как содержимого обрабатываемых операндов, так и временного фактора при формировании выходной реакции отдельного нейрона и при распространении "спайков" по нейросети, что, как показывает нейрофизиологический опыт [253, 254], весьма существенно для работы реальных нейронов и нейронных ансамблей.

Пусть задана упорядоченная по целочисленному времени конечная последовательность векторов 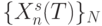с целочисленными компонентами.

Будем говорить, что 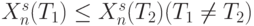, если при некотором фиксированном весовом векторе 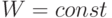покомпонентная свертка этих векторов находится в том же отношении ; а рангом вектора 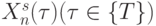в последовательности 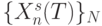будем называть число:

( 8.14)

где суммирование ведется по всем 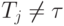, а

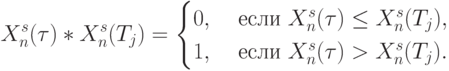
В простейшем случае ранг входного вектора 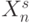равен лексикографическому индексу , если "скользящее окно" 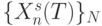в любой момент времени содержит ровно по одному вектору из полного набора входных векторов .

Пусть конечная последовательность векторов 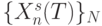(через время начальной задержки ) смещается по "бесконечной" последова-тельности 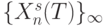таким образом, что вектор появляется вместо вектора 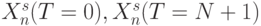- вместо вектора 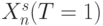и так далее. В результате такого "скольжения" 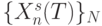по бесконечной последовательности 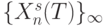формируется последовательность рангов .

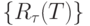Определим систему решающих правил, которые настраивает ранготрон на реализацию функции 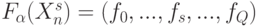, считая компоненты вектора порогов 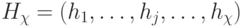заданными на множестве рангов :

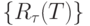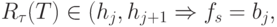( 8.15)

где , , ,

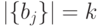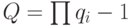
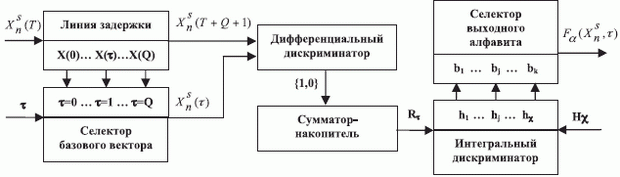
Отвечающая (8.14) и (8.15) структурно-функциональная схема ран-готрона включает (рис. 8.8): линию задержки с выводами для фиксации базовой -позиции, по отношению к которой вычисляются 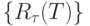; управляемый извне селектор базового вектора 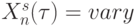; дифферен-циальный дискриминатор, который последовательно (по ) сравнивает базовый вектор 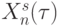со всеми элементами текущего "скользящего окна" 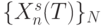; сумматор-накопитель, который формирует последовательность рангов 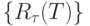; интегральный дискриминатор, который фиксирует принадлежность текущего значения ранга одному из возможных пороговых полуинтервалов ; блок подстановки значений дискретной функции 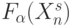по правилам (8.15).

Такой ранготрон в принципе не может работать без начальной задержки хотя бы на один входной вектор, и он адаптивен по определению, так как ранг любого входного вектора определяется по отношению к той совокупности входных векторов, которые попали в "скользящее окно"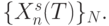

Проиллюстрируем работу ранготрона на примере класса булевых функций 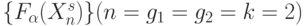таблицы 8.6.

Будем считать, что накопленная в линии задержки ранготрона после-довательность 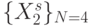содержит полный набор двумерных булевых векторов 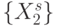, а процесс смещения такого "скользящего окна" по "бесконечной" последовательности 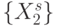эквивалентен циклическому сдвигу 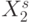в

Таблица 8.6. Тривиальная alpha-нумерация булевых функций

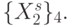
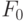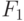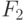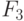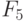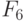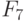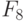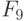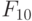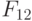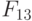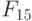0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	2	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	3	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

увеличить изображение
Рис. 8.8. Структурно-функциональная схема ранготрона

Тогда совокупности различных состояний линии задержки ранготрона будет отвечать подгруппа циклических сдвигов с образующей, формируемой в период начальной загрузки линии задержки. Если образующая упорядочена в лексикографическом порядке, то разнообразие внутренних состояний линии задержки ранготрона описывается матрицей циклического сдвига векторов :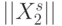

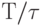	0	1	2	3
0	(0,0)	(ОД)	(1,0)	(1,1)
1	(1,1)	(0,0)	(0,1)	(1,0)
2	(1,0)	(1,1)	(0,0)	(ОД)
3	(0,1)	(1,0)	(1,1)	(0,0)

Здесь элементы строки однозначно связаны с тактом задержки , а элементы столбца - с тактом смещения 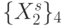по бесконечной последовательности .

Зафиксируем базовую позицию в линии задержки ранготрона, по отношению к которой вычисляется последовательность рангов 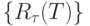. Тогда согласно (8.14) входная последовательность 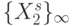, отвечающая требованиям матрицы 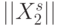, порождает последовательность рангов , , , 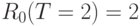и так далее в цикле начиная с .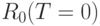

Пусть модифицируемая извне система решающих правил имеет вид:

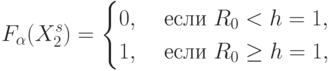( 8.16)

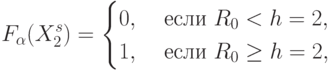( 8.17)

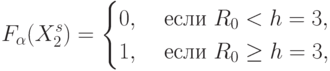( 8.18)

Каждое из правил (8.16)-(8.18) применимо одновременно ко всем столбцам матрицы 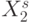, и поэтому можно считать, что в ранготроне одновременно реализуются следующие булевы функции:

• при настройке на правило (8.16):

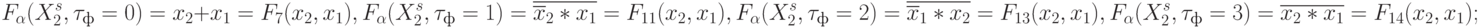
  ( x_2,x_1)

• при настройке на правило (8.17):
  
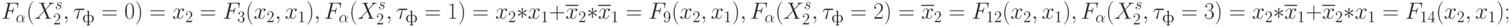
• при настройке на правило (8.18):
  

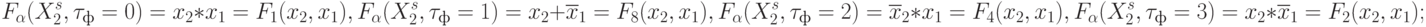
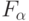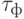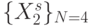Здесь нижний индекс булевой функции соответствует ее -нумерации таблицы 2, фиксирует положение вектора в "скользящем окне" , по отношению к которому "интерпретируется" отображение 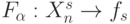, а ( ) и ( 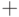) - соответственно логическое умножение и сложение.

Отсюда, "булев" ранготрон на циклически сдвигаемой входной последовательности с фиксированной образующей является практически полным логическим модулем по отношению к классу двумерных булевых функций. При этом коэффициент "виртуального" (конвейерного) распараллеливания вычислений (по "входу") в ранготроне равен . Виртуальность в данном случае означает, что выполняемое ранготроном отображение в каждый момент времени имеет вид 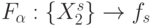, так как система решающих правил (8.16)-(8.18) распространяется на все 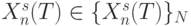в каждый момент времени , несмотря на то что текущий ранг 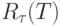, а с ним и определяются по содержимому базовой позиции 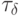.