|
Входит ли данный курс в перечень программы по переподготовки ФСТЭК? |
Измерение формы и спектра сигналов
Общие сведения
Радиотехнические сигналы при взаимодействии друг с другом или с помехой, а также проходя через устройства, содержащие нелинейные элементы, претерпевают изменение формы и спектра. При взаимодействии сигналов возникает модуляция и значение искажений необходимо измерять форму сигнала и его спектр.
Измерение спектра предусматривает определение большого числа гармонических составляющих, которое при исследовании непериодических сигналов стремится к бесконечности.
Спектральная функция импульсного сигнала х(t) представляет собой комплексную функцию вида
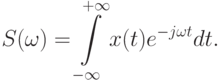 |
( 10.1) |
Измерения выполняются в течение некоторого интервала времени T, поэтому формула (10.1) преобразуется в следующую:
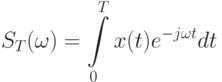 |
( 10.2) |
Из рассмотрения формулы (10.2) видно, что измеряемый спектр является функцией частоты и интервала времени измерения. Функцию 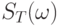 называют текущим спектром сигнала. Очевидно, что с увеличением интервала времени измерения текущий спектр приближается к истинному.
называют текущим спектром сигнала. Очевидно, что с увеличением интервала времени измерения текущий спектр приближается к истинному.
Для определения спектра периодического несинусоидального сигнала необходимо измерить амплитуды и частоты его гармонических составляющих. Для этой цели применяют приборы – анализаторы гармоник и анализаторы спектра – как с ручным управлением, так и автоматические. Гармонические составляющие можно измерять поочередно или одновременно; первый способ анализа спектра называют последовательным, а второй – параллельным.
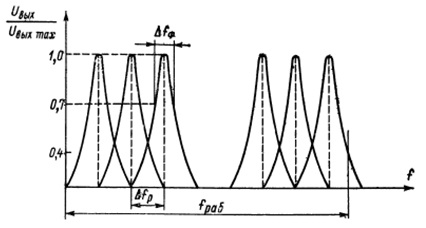
Основными характеристиками анализаторов являются разрешающая способность и время анализа. Разрешающая способность 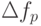 определяется минимальным расстоянием по оси частот, при котором можно выделить и измерить с заданной погрешностью две соседние составляющие спектра. Разрешающая способность прямо пропорциональна полосе пропускания фильтра
определяется минимальным расстоянием по оси частот, при котором можно выделить и измерить с заданной погрешностью две соседние составляющие спектра. Разрешающая способность прямо пропорциональна полосе пропускания фильтра 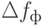 избирательного контура (рис. 10.1
рис.
10.1):
избирательного контура (рис. 10.1
рис.
10.1):
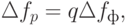 |
( 10.3) |
где 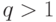 .
.
В автоматических анализаторах на разрешающую способность влияют переходные процессы. Время, в течении которого характеристика анализатора приближается к его статистической, называют временем установления 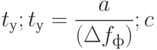 , где a – коэффициент, близкий к единице; значение a зависит от типа применяемого избирательного контура или фильтра.
, где a – коэффициент, близкий к единице; значение a зависит от типа применяемого избирательного контура или фильтра.
Время анализа анализаторами параллельного действия соизмеримо со временем установления:
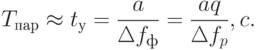 |
( 10.4) |
Скорость анализа определяется отношением рабочего диапазона частот анализатора fраб (рис. 10.1 рис. 10.1) к времени анализа:
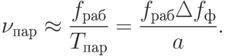 |
( 10.5) |
Обозначив  , где
, где 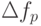 – разрешающая способность резонатора, определяемая формулой (10.3), получаем выражение для скорости параллельного анализа
– разрешающая способность резонатора, определяемая формулой (10.3), получаем выражение для скорости параллельного анализа
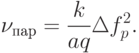
Скорость последовательного анализа определяется уравнением  или, с учетом ранее приведенных соотношений,
или, с учетом ранее приведенных соотношений,
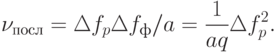
 |
( 10.6) |
т.е. оно в k раз больше, чем при параллельном анализе.