Координатные преобразования в OpenGL

Стек матриц

При формировании изображений часто возникает необходимость сохранения содержания текущей матрицы и затем восстановления её значения. Для этого OpenGL реализует стек матриц, который функционирует по принципу "последним пришел – первым ушел". Для видовой и проекционной матриц OpenGL реализует отдельные стеки. Размер этих стеков различается. Для видовой матрицы размер стека составляет не менее 32 матриц, для проекционной – не менее 2 матриц. Некоторые реализации библиотеки могут иметь больший размер этих стеков. Небольшой размер стека проекционных матриц объясняется тем, что проекционные матрицы редко используются для реализации композиции преобразований. Текущий стек матриц изменяется при изменении типа текущей матрицы с помощью команды MatrixMode, поэтому текущая видовая матрица может быть скопирована только в стек видовых матриц, текущая проекционная матрица соответственно может быть скопирована только в стек проекционных матриц.

Для копирования текущей матрицы в соответствующий её типу стек матриц используется команда PushMatrix.

C#:
  void PushMatrix();
Object Pascal:
  procedure glPushMatrix;

Если на момент вызова команды стек уже заполнен, то копия текущей матрицы в стек добавлена не будет и библиотека сгенерирует ошибку переполнения стека:

C#:
  ErrorCode.StackOverflow
Object Pascal:
  GL_STACK_OVERFLOW

Которую можно проанализировать с помощью команды GetError:

C#:
  ErrorCode GetError();
Object Pascal:
  function  glGetError: GLenum;

Для извлечения последней матрицы из стека в текущую матрицу используется команда PopMatrix:

C#:
  void PopMatrix();
Object Pascal:
  procedure glPopMatrix;

Если стек пуст, то текущая матрица не будет изменена, а библиотека сгенерирует ошибку:

C#:
  ErrorCode.StackUnderflow
Object Pascal:
  GL_STACK_UNDERFLOW

Которую можно проанализировать с помощью команды GetError.

Краткие итоги

В лекции рассмотрены основные команды для выполнения видовых и перспективных преобразований, а также команды универсального назначения для преобразования матриц OpenGL. Рассмотрены особенности выполнения комбинаций преобразований с использованием матриц OpenGL, ситуации в которых комбинации преобразований являются аддитивными и мультипликативными. Показаны варианты определения результатов видовых преобразований. Рассмотрены особенности формирования параллельной и перспективной центральной проекции.

Упражнения. Построение поверхностей вращения

Пример выполнения задания

Задание: Постройте изображение цилиндра, используя в качестве основных примитивов четырехугольники с общими гранями.

Выполнение задания

В качестве основы для программы можно использовать программу, созданную в "Структура приложений, использующих OpenGL" . Для формирования цилиндра можно использовать координаты точек на двух окружностях, которые расположены, например, вдоль оси OZ. Сами окружности будут располагаться параллельно плоскости XOY. Для расчёта координат точек на окружности можно использовать уравнения:

Где 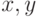– координаты точки на окружности, - угол поворота радиус-вектора вокруг центра окружности в плоскости её построения, – радиус окружности.

Построение точек на окружности будет выполняться в цикле.

Так как все грани цилиндра будут одного цвета, и он строится без использования освещения, то в программе будет предусмотрено переключение между режимами отображения многоугольников: отображаемых в виде закрашенных фрагментов и отображение только граней четырехугольников. Для этого необходимо объявить глобальную переменную, которая и будет определять режим отображения примитивов.

C#:
    PolygonMode mode = PolygonMode.Fill;
Object Pascal:
  var
    mode: GLenum = GL_FILL;

Для изменения режима отображения будет использоваться команда PolygonMode.

Формирование изображения многоугольника будет выполняться с помощью фрагмента кода:

C#:

private void glControl1_Paint(object sender, PaintEventArgs e)
{
…
  GL.PolygonMode(MaterialFace.FrontAndBack, mode);
  GL.Begin(BeginMode.QuadStrip);
  double r = 0.5;
  int n = 20;
  for (int i = 0; i <= n; ++i)
  {
    double a = 2 * Math.PI/n * i;
    double x = r * Math.Cos(a);
    double y = r * Math.Sin(a);
    GL.Vertex3(x, y, -0.5);
    GL.Vertex3(x, y, 0.5);
  }
  GL.End();
…
}

Object Pascal:

procedure TfrmMain.FormPaint(Sender: TObject);
  var
  i, n: integer;
  x, y, r, a: double;
begin
…
  glPolygonMode(GL_FRONT_AND_BACK, mode);
  glBegin (GL_QUAD_STRIP);
  r := 0.5;
  n := 20;
  for i := 0 to n do
  begin
    a := 2*pi/n * i;
    x := r * Cos(a);
    y := r * Sin(a);
    glVertex3d(x, y, -0.5);
    glVertex3d(x, y, 0.5);
  end;
  glEnd; 
…
end;

Для изменения режима отображения примитивов будут использоваться клавиши F1 и F2.

C#:

private void glControl1_KeyDown(object sender, KeyEventArgs e)
{
  switch(e.KeyCode)
  {
    case Keys.Insert:   AngleX += AngleDl; break;
    case Keys.Delete:   AngleX -= AngleDl; break;
    case Keys.Home:     AngleY += AngleDl; break;
    case Keys.End:      AngleY -= AngleDl; break;
    case Keys.Prior:    AngleZ += AngleDl; break;
    case Keys.Next:     AngleZ -= AngleDl; break;
    case Keys.F1: mode = PolygonMode.Fill; break;
    case Keys.F2: mode = PolygonMode.Line; break;
  }
  glControl1.Invalidate(); 
}

Object Pascal:

procedure TfrmMain.FormKeyDown(Sender: TObject; var Key: Word;
  Shift: TShiftState);
begin
 if Key = VK_ESCAPE then Close;
 case Key of
   VK_INSERT: inc(AngleX, AngleDl);
   VK_DELETE: dec(AngleX, AngleDl);
   VK_HOME:   inc(AngleY, AngleDl);
   VK_END:    dec(AngleY, AngleDl);
   VK_PRIOR:  inc(AngleZ, AngleDl);
   VK_NEXT:   dec(AngleZ, AngleDl);
   VK_F1: mode := GL_FILL;
   VK_F2: mode := GL_LINE;
 end;
 InvalidateRect(Handle, nil, False);
end;

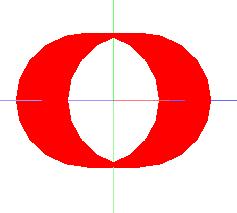
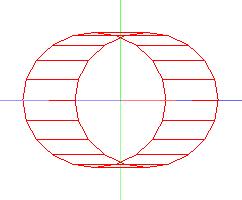
На рис. 5.11 и рис. 5.12 показан вид цилиндра при режимах отображения граней примитивов PolygonMode.Fill/GL_FILL и PolygonMode.Line/GL_LINE.

Рис. 5.11. Вид цилиндра при режиме отображения граней примитивов PolygonMode.Fill(C#)/GL_FILL (Object Pascal)

Рис. 5.12. Вид цилиндра при режиме отображения граней примитивов PolygonMode.Line(C#)/GL_LINE(Object Pascal)

Задания

1. Постройте изображение тора, используя в качестве основных примитивов треугольники с общими гранями.
2. Постройте изображение тора, используя в качестве основных примитивов четырехугольники с общими гранями.
3. Постройте поверхность вращения на основе графика функции лемниската Бернули, уравнение которой в полярной системе координат:
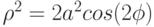
4. Постройте изображение конуса, используя в качестве основных примитивов треугольники с общими гранями.
5. Постройте изображение сферы, используя в качестве основных примитивов четырехугольники с общими гранями.
6. Постройте поверхность вращения на основе графика функции розы, уравнение которой в полярных координатах .
7. Постройте изображение цилиндра, используя в качестве основных примитивов треугольники с общими гранями.
8. Постройте поверхность вращения на основе графика функции, уравнение которой .
9. Постройте поверхность вращения на основе графика функции эллипса .
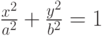