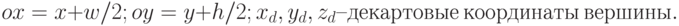Координатные преобразования в OpenGL

Проекционные преобразования

Проекционные преобразования определяются матрицей проекции и выполняются после видовых преобразований ( рис. 5.3).

Матрица проекции выполняет несколько функций:

1. Ограничивает область видимости объемной сцены. Для этого в командах Ortho и Frustum в качестве параметров передаются три пары координат для трех осей координат. С ограничением области вывода неразрывно связана операция усечения координат. Результатом этого преобразования является преобразование координат вершин видимой области сцены для каждой из осей координат, таким образом, чтобы они находились в интервале от –1 до 1.
2. Определяет перспективные преобразования.
3. Выполняет преобразование мировой (правосторонней) системы координат ( рис. 5.1) в видовую (левостороннюю) систему координат ( рис. 5.2). Преобразование заключается в изменении направления оси OZ на противоположное.

Результатом умножения видовых координат вершин на матрицу проекций является получение усеченных координат вершин видимой области, лежащих в интервале от -1 до 1 для каждой из осей координат.

Параллельная проекция

Для формирования матрицы параллельной проекции используется команда

Ortho(l, r, b, t, n, f: GLdouble)

Команда имеет шесть параметров. Каждая пара параметров определяет координаты границ области видимости для каждой из осей координат:

l, r – левая и правая границы области видимости вдоль оси OX;

b, t – нижняя и верхняя границы области видимости вдоль оси OY;

n, f – ближняя и дальняя границы области видимости вдоль оси OZ.

Фактически параметры команды определяют расположение граничных плоскостей, ограничивающих видимую область пространства.

Команда Ortho формирует матрицу:

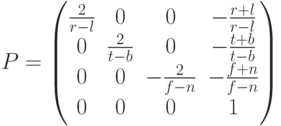
Диагональные элементы матрицы выполняют усечение каждой из осей координат в соответствии с границами области видимости, определяемой командой Ortho. В результате координаты видимой области находятся в интервале [-1;1] для каждой из осей. Поэтому диагональные элементы имеют вид дроби с числом 2 в качестве числителя (длина области видимости в усеченных координатах) и знаменателя, который равен длине области видимости в мировых координатах.

Элемент в третьем столбце матрицы имеет отрицательный знак для изменения направления оси OZ на противоположное, и преобразует мировую систему координат в видовую.

Элементы матрицы четвертого столбца переносят изображение в центр системы координат с учётом усечения координат.

Центр сцены для параллельной проекции имеет координаты:

Формируемая командой Ortho матрица () умножается на текущую матрицу (M результирующая матрица (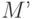) заменяет текущую матрицу:

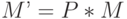
Перспективная проекция

Для задания центральной перспективной проекции в OpenGL используется команда Frustum:

Frustum (l, r, b, t, n, f: GLdouble);

Команда Frustum имеет шесть параметров, которые определяют граничные координаты области видимости:

• l, r – левая и правая границы области видимости вдоль оси OX;
• b, t – нижняя и верхняя границы области видимости вдоль оси OY;
• n, f – ближняя и дальняя границы области видимости вдоль оси OZ.

Ближняя граница оси OZ (параметр n) так же определяет положение плоскости проекции, которая располагается перпендикулярно оси OZ.

Точка наблюдения находится в начале координат. Видимый объем представляет собой усеченную пирамиду, проекция видимой области формируется на плоскости усечения, перпендикулярной оси OZ. Значения l, r, b, t задаются для ближней к наблюдателю плоскости отсечения. Значения n и f должны быть положительными.

Команда Frustum формирует матрицу ():

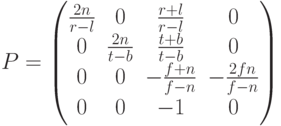
При выполнении команды Frustum матрица перспективной проекции () умножается на текущую матрицу (), и результирующая матрица (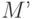) замещает текущую матрицу:

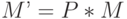
Центр сцены имеет координаты:

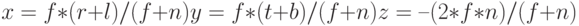
После умножения на матрицу проекции координаты вершин будут в интервале [-1,1] для всех осей координат.

Эффект перспективы зависит от расстояния ближней плоскости до наблюдателя. Чем ближе плоскость проекции расположена к точке наблюдения, тем больше эффект перспективы.

Определение области вывода

На последнем этапе координатных преобразований вычисляются координаты области вывода. Координаты области вывода определяются с помощью команды:

Viewport (x,y: GLint; w, h: GLsizei);

Команда имеет четыре параметра:

• x, y – координаты верхнего левого угла области вывода;
• w, h – ширина и высота области вывода.

Оконные координаты проекции вычисляются как

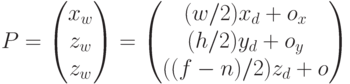
где – координаты центра области вывода изображения: