Координатные преобразования в OpenGL

Пример координатных преобразований

Рассмотрим преобразования, которые выполняет OpenGL при построении изображения квадрата, который формируются в листинге 5.1 на языке C# с использованием библиотеки OpenTK и в листинге 5.2 на языке Object Pascal.

private void glControl1_Paint(object sender, PaintEventArgs e)
{
  GL.ClearColor(0.5f, 0.5f, 0.75f, 1.0f); // цвет фона
  // очистка буферов цвета и глубины
  GL.Clear(ClearBufferMask.ColorBufferBit | ClearBufferMask.DepthBufferBit);
  // поворот изображения
  GL.LoadIdentity();
  GL.Rotate(AngleX, 1.0, 0.0, 0.0);
  GL.Rotate(AngleY, 0.0, 1.0, 0.0);
  GL.Rotate(AngleZ, 0.0, 0.0, 1.0);
  // формирование осей координат
  GL.Begin(BeginMode.Lines);
  GL.Color3(1f, 0f, 0f); GL.Vertex3(-10, 0, 0); GL.Vertex3(10, 0, 0);
  GL.Color3(0f, 1f, 0f); GL.Vertex3(0, -10, 0); GL.Vertex3(0, 10, 0);
  GL.Color3(0f, 0f, 1f); GL.Vertex3(0, 0, -10); GL.Vertex3(0, 0, 10);
  GL.End();
  // видовые преобразования
  GL.Rotate(45, 0, 0, 1);
  GL.Translate(5, 0, 0);
  // формирования квадрата
  GL.Color3(0f, 0f, 1f); // цвет фона
  GL.Rect(-1f, -1f, 1f, 1f);
  // завершение формирования изображения
  GL.Flush();
  GL.Finish();
  glControl1.SwapBuffers();
}
private void glControl1_Resize(object sender, EventArgs e)
{
  GL.Viewport(0, 0, glControl1.Width, glControl1.Height);
  GL.MatrixMode(MatrixMode.Projection);
  GL.LoadIdentity();
  GL.Ortho(-10, 10, -10, 10, -10, 10);
  GL.MatrixMode(MatrixMode.Modelview);
  glControl1.Invalidate();
}

procedure TfrmGL.FormPaint(Sender: TObject);
begin
  glClearColor (1, 1, 1, 1); // цвет фона
  glClear (GL_COLOR_BUFFER_BIT or GL_DEPTH_BUFFER_BIT);
  // установка видовой матрицы в качестве текущей
  glMatrixMode(GL_MODELVIEW);
  // установка видовой матрицы единичной
  glLoadIdentity;
  // формирование осей координат
  glBegin (GL_LINES);
    glColor3f(1, 0, 0); glVertex3f (-10, 0, 0); glVertex3f (10, 0, 0);
    glColor3f(0, 1, 0); glVertex3f (0, -10, 0); glVertex3f (0, 10, 0);
    glColor3f(0, 0, 1); glVertex3f (0, 0, -10); glVertex3f (0, 0, 10);
  glEnd;
  // видовые преобразования
  glRotatef(45, 0, 0, 1);
  glTranslate(5, 0, 0);
  // формирования квадрата
  glColor (0, 0, 0, 1); // цвет фона
  glRectd(-1, -1, 1, 1);
  // завершение формирования изображения
  glFlush;
  glFinish;
  SwapBuffers(DC);
end;
procedure TfrmGL.FormResize(Sender: TObject);
begin
  // определение области вывода
  glViewport(0, 0, ClientWidth, ClientHeight);
  // задание матрицы проекции
  glMatrixMode(GL_PROJECTION);
  glLoadIdentity;
  glOrtho(-10, 10, -10, 10, -10, 10);
  // перерисовка изображения
  InvalidateRect(Handle, nil, False);
end;

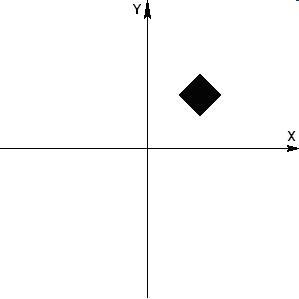
В программе используются преобразования параллельного переноса и вращения вокруг оси OZ. Результат работы программы представлен на рис. 5.4 Дополнительно на рисунке изображены направления осей координат OX и OY.

Рис. 5.4. Пример координатных преобразований

Рассмотрим формирование видовой матрицы, которое выполняется при формировании изображения. Видовая матрица является текущей после выполнения команды MatrixMode:

C#:
  GL.MatrixMode(MatrixMode.Modelview);
Object Pascal:
  glMatrixMode(GL_MODELVIEW);

Перед формированием изображения видовой матрице задается единичное значение с помощью команды LoadIdentity. Вызов команды Rotate формирует матрицу поворота () вокруг оси OZ:

C#:
  GL.Rotate(45, 0, 0, 1);
Object Pascal:
  glRotatef(45, 0, 0, 1);

Эта матрица умножается на видовую матрицу (), полученная матрица становится текущей ():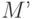

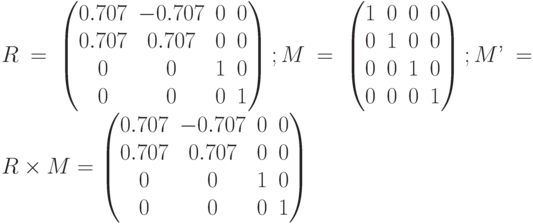
Команда Translate формирует матрицу параллельного переноса () и умножает её на видовую матрицу (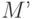), результирующая матрица (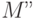) становится текущей:

C#:
GL.Translate(5, 0, 0);
Object Pascal:
glTranslate(5, 0, 0);

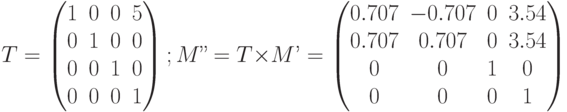
Матрица проекций формируется в методе glControl1_Paint в программе на C# и в процедуре FormResize в программе на Object Pascal. В программе используется параллельная проекция, определяемая с помощью команды Ortho. После выбора матрицы проекции в качестве текущей с помощью команды MatrixMode её значение устанавливается единичным с помощью команды LoadIdentity:

C#:
GL.MatrixMode(MatrixMode.Projection);
GL.LoadIdentity();
Object Pascal:
glMatrixMode(GL_PROJECTION);
glLoadIdentity;

Команда Ortho формирует матрицу параллельной проекции (P), которая умножается на текущую матрицу проекции. Результирующая матрица становится новой матрицей проекции. Так как на момент вызова команды Ortho матрица проекции является единичной, то значение результирующей матрицы совпадает со значением матрицы, формируемой командой Ortho.

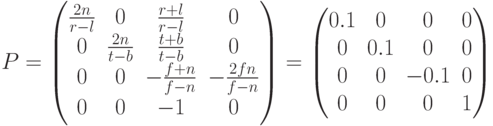
Рассчитаем координаты проекции одной из вершин квадрата с координатами (-1,-1,0). После видового преобразования координаты точки будут иметь значения:

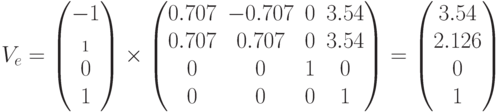
После умножения видовых координат вершин на матрицу проекций получаются усечённые координаты вершин, которые имеют значения:

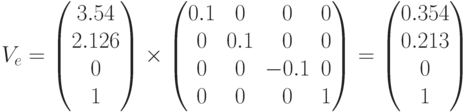
Полученные значения преобразуются в координаты области вывода, которые определяются командой Viewport:

C#:
  GL.Viewport(0, 0, glControl1.Width, glControl1.Height);
Object Pascal:
  glViewport(0, 0, ClientWidth, ClientHeight);

В рассматриваемом примере ширина и высота клиентской области формы одинаковы и равны 300 пикселов.

После преобразования в координаты области вывода, координаты проекции вершины принимают значения:

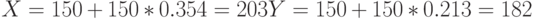
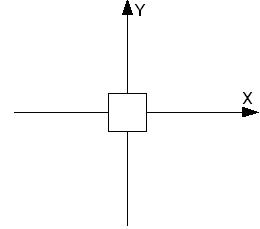
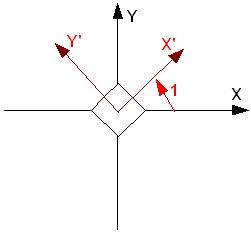
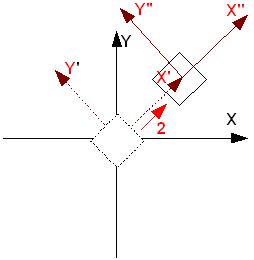
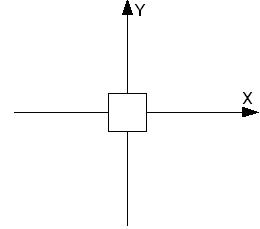
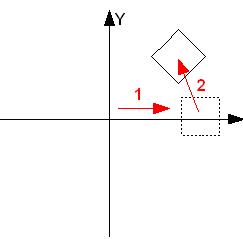
Для наглядного представления выполняемых преобразований обычно используют два варианта рассмотрения преобразований. В первом варианте видовые преобразования изменяют положение локальной системы координат объекта, и следующее преобразование выполняется уже относительно измененной системы координат. Порядок преобразований в этом случае совпадает с порядком вызова команд преобразования видовой матрицы. На рис. 5.5, рис. 5.6, рис. 5.7 показан такой вариант преобразований. Первое преобразование поворота вокруг оси OZ на 45° изменяет направление осей OX и OY локальной системы координат ( рис. 5.6). Преобразование сдвига меняет положение объекта относительно преобразованной локальной системы координат объекта X’OY’ ( рис. 5.7).

Рис. 5.5. Исходное положение объекта

Рис. 5.6. Положение объекта после преобразования поворота

Рис. 5.7. Положение объекта после преобразования сдвига

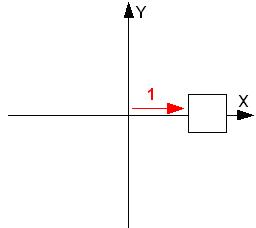
Во втором варианте система координат остается неподвижной, и все преобразования выполняются в исходной системе координат. Для того чтобы получить результат выполнения преобразований необходимо представить выполнение видовых преобразований в порядке обратном вызову соответствующих команд в программе. Например, для выше приведенного примера порядок преобразований необходимо рассматривать в следующем порядке: сначала перенос, а затем поворот вокруг оси OZ ( рис. 5.8, рис. 5.9, рис. 5.10).

Рис. 5.8. Исходное положение объекта

Рис. 5.9. Положение объекта после преобразования сдвига

Рис. 5.10. Положение объекта после преобразования поворота