|
Подскажите, пожалуйста, планируете ли вы возобновление программ высшего образования? Если да, есть ли какие-то примерные сроки? Спасибо! |
Координатные преобразования в OpenGL
Параллельный перенос
Для выполнения параллельного переноса библиотека реализует команду Translate[f d]. Команда имеет три параметра, определяющие координаты вектора параллельного переноса. Команда Translate формирует матрицу параллельного переноса и умножает её на текущую матрицу OpenGL.
При выполнении команды Translate формируется вертикальная матрица:
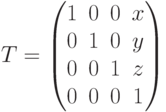
где 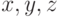 – координаты вектора параллельного переноса.
– координаты вектора параллельного переноса.
Полученная матрица ( ) умножается на текущую матрицу библиотеки (
) умножается на текущую матрицу библиотеки ( ), и результирующая матрица (
), и результирующая матрица (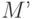 ) заменяет текущую матрицу OpenGL:
) заменяет текущую матрицу OpenGL:
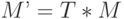
В результате преобразование параллельного переноса добавляется к тем преобразованиям, которые выполняла текущая матрица на момент вызова команды Translate.
В библиотеке OpenTK команда реализована как ряд статических методов класса GL (C#):
void Translate(Vector3 trans); void Translate(Vector3d trans); void Translate(double x, double y, double z); void Translate(float x, float y, float z);
В Object Pascal в файле OpenGL.pas объявлено несколько процедур, которые реализуют эту команду, и различаются только типом параметров:
procedure glTranslated (x,y,z: GLdouble); procedure glTranslatef (x,y,z: GLfloat); procedure glTranslate(x,y,z: GLdouble); overload; procedure glTranslate(x,y,z: GLfloat); overload;
Масштабирование относительно начала координат
Для выполнения операции масштабирования относительно начала координат используется команда Scale[f d]. Команда имеет три параметра, которые определяют коэффициенты масштабирования для каждой из осей координат. Команда формирует матрицу:
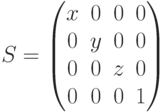
В результате выполнения команды Scale матрица масштабирования ( ) умножается на текущую матрицу (
) умножается на текущую матрицу ( ), и результирующая матрица (
), и результирующая матрица (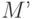 ) заменяет текущую матрицу:
) заменяет текущую матрицу:
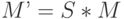
В результате к преобразованиям, выполняемым текущей матрицей перед вызовом команды Scale, добавляется еще преобразование масштабирования.
В библиотеке OpenTK команда реализована как ряд статических методов класса GL (C#):
void Scale(Vector3 scale); void Scale(Vector3d scale); void Scale(double x, double y, double z); void Scale(float x, float y, float z);
В Object Pascal команда реализуется с помощью процедур, которые различаются типом используемых параметров:
procedure glScaled (x,y,z: GLdouble); procedure glScalef (x,y,z: GLfloat); procedure glScale(x,y,z: GLdouble); overload; procedure glScale(x,y,z: GLfloat); overload;
Поворот вокруг произвольной оси в пространстве
Преобразование поворота вокруг произвольной оси в пространстве может быть выполнено с помощью команды Rotate[f d].
В OpenTK команда реализована как ряд статических методов класса GL (C#):
void Rotate(double angle, Vector3d axis); void Rotate(float angle, Vector3 axis); void Rotate(double angle, double x, double y, double z); void Rotate(float angle, float x, float y, float z);
В Object Pascal команда реализуется с помощью процедур, которые различаются типом параметров:
procedure glRotated (angle, x,y,z: GLdouble); procedure glRotatef (angle, x,y,z: GLfloat); procedure glRotate(angle, x,y,z: GLdouble); overload; procedure glRotate(angle, x,y,z: GLfloat); overload;
Параметры x, y, z задают координаты вектора, вокруг которого выполняется поворот. Первый параметр angle определяет угол поворота в градусах вокруг вектора против часовой стрелки, если смотреть вдоль отрицательного направления вектора поворота. Необходимо обратить внимание на то, что угол поворота задается в градусах, в отличие от параметров различных тригонометрических функций в Object Pascal.
Как и при выполнении команд Translate и Scale, при выполнении команды Rotate библиотека формирует матрицу преобразования ( ), которая умножается на текущую матрицу (
), которая умножается на текущую матрицу ( ), результирующая матрица (
), результирующая матрица (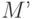 ) затем становится текущей матрицей.
) затем становится текущей матрицей.
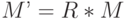
Преобразование поворота вокруг произвольного вектора в пространстве является сложным преобразованием. На практике часто используют комбинацию преобразований из поворотов вокруг осей координат. Ниже приведены матрицы, выполняющие повороты вокруг осей координат.
 |
 |
 |
glRotated(a, 1,0,0) GL.Rotate(a, 1,0,0) |
glRotated(a, 0,1,0) GL.Rotate(a, 0,1,0) |
glRotated(a, 0,0,1) GL.Rotate(a, 0,0,1) |
Композиция преобразований
Последовательное выполнение нескольких преобразований можно представить в виде единой матрицы суммарного преобразования. Умножение на единственную матрицу выполняется быстрее, чем последовательное умножение координат каждой вершины на несколько матриц.
Матрица суммарного преобразования может быть получена умножением матриц отдельных преобразований. В общем случае результат произведения матриц зависит от порядка их умножения и не является аддитивным. Т. е. результат преобразований, который описывается матрицами, в общем случае зависит от последовательности выполнения преобразований.
При выполнении некоторых однотипных преобразований произведение матриц может быть аддитивной или мультипликативной операцией и результат выполнения таких операций не будет зависеть от порядка их выполнения. К таким преобразованиям, в частности, относятся видовые преобразования: параллельный перенос, масштабирование относительно начала координат, поворот вокруг произвольного вектора.
Две последовательные операции параллельного переноса являются аддитивными. Результат выполнения этих операций не зависит от порядка их выполнения. Например, результат последовательного сдвига точки P0 на расстояние ( ) в точку P1, а затем сдвига точки P1 на расстояние (
) в точку P1, а затем сдвига точки P1 на расстояние ( ) в точку P2 не зависит от порядка умножения матриц
) в точку P2 не зависит от порядка умножения матриц 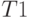 и
и  которые описывают каждую из операций сдвига:
которые описывают каждую из операций сдвига:
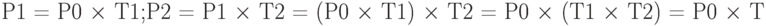
Суммарный перенос, вычисленный как произведение матриц, аддитивен:
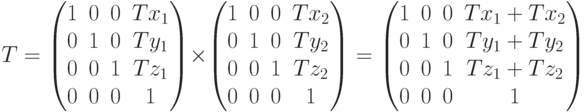
Последовательное выполнение операций масштабирования является мультипликативной операцией. Например, результат последовательного выполнения двух операции масштабирования с коэффициентами ( ) и (
) и ( ) не зависит от порядка их выполнения. Если обозначить через
) не зависит от порядка их выполнения. Если обозначить через 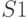 и
и 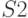 матрицы масштабирования, получим:
матрицы масштабирования, получим:
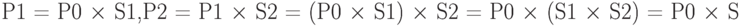
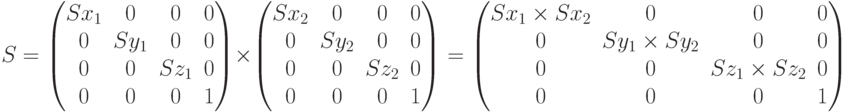
Из вычисления видно, что результирующее масштабирование, вычисленное как произведение матриц, мультипликативно и не зависит от порядка умножения матриц.
Аналогичным образом можно показать, что два последовательных поворота вокруг осей координат аддитивны.
