Нейронные сети ассоциативной памяти
Сети Хопфилда
Наиболее известной сетью ассоциативной памяти является сеть Хопфилда [8.1]. В основе сети Хопфилда лежит следующая идея - запишем систему дифференциальных уравнений для градиентной минимизации "энергии" H (функции Ляпунова). Точки равновесия такой системы находятся в точках минимума энергии. Функцию энергии будем строить из следующих соображений:
- Каждый эталон должен быть точкой минимума.
- В точке минимума все координаты образа должны иметь значения
 .
.
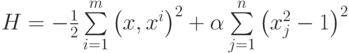
не удовлетворяет этим требованиям строго, но можно предполагать, что первое слагаемое обеспечит притяжение к эталонам (для вектора x фиксированной длины максимум квадрата скалярного произведения 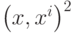 достигается при x=xi ), а второе слагаемое
достигается при x=xi ), а второе слагаемое 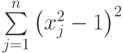 - приблизит к единице абсолютные величины всех координат точки минимума. Величина
- приблизит к единице абсолютные величины всех координат точки минимума. Величина  характеризует соотношение между этими двумя требованиями и может меняться со временем.
характеризует соотношение между этими двумя требованиями и может меняться со временем.
Используя выражение для энергии, можно записать систему уравнений, описывающих функционирование сети Хопфилда:
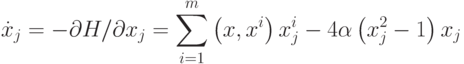 |
( 1) |
Сеть Хопфилда в виде (1) является сетью с непрерывным временем. Это, быть может, и удобно для некоторых вариантов аналоговой реализации, но для цифровых компьютеров лучше воспользоваться сетями, функционирующими в дискретном времени - шаг за шагом.
Построим сеть Хопфилда с дискретным временем. Сеть должна осуществлять преобразование входного вектора  так, чтобы выходной вектор
так, чтобы выходной вектор  был ближе к тому эталону, который является правильным ответом. Преобразование сети будем искать в следующем виде:
был ближе к тому эталону, который является правильным ответом. Преобразование сети будем искать в следующем виде:
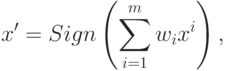 |
( 2) |
где 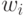 - вес
- вес  -го эталона, характеризующий его близость к вектору
-го эталона, характеризующий его близость к вектору  ,
, 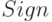 - нелинейный оператор, переводящий вектор с координатами
- нелинейный оператор, переводящий вектор с координатами  в вектор с координатами
в вектор с координатами 
Функционирование сети. Сеть работает следующим образом:
- На вход сети подается образ
 , а на выходе снимается образ
, а на выходе снимается образ  .
. - Если
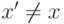 , то полагаем
, то полагаем 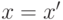 и возвращаемся к шагу 1.
и возвращаемся к шагу 1. - Полученный вектор
 является ответом.
является ответом.
Таким образом, ответ всегда является неподвижной точкой преобразования сети (2) и именно это условие (неизменность при обработке образа сетью) и является условием остановки.
Пусть 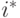 - номер эталона, ближайшего к образу
- номер эталона, ближайшего к образу  . Тогда, если выбрать веса пропорционально близости эталонов к исходному образу
. Тогда, если выбрать веса пропорционально близости эталонов к исходному образу  , то следует ожидать, что образ
, то следует ожидать, что образ  будет ближе к эталону
будет ближе к эталону  , чем
, чем  , а после нескольких итераций он станет совпадать с эталоном
, а после нескольких итераций он станет совпадать с эталоном  .
.
Наиболее простой сетью вида (2) является дискретный вариант сети Хопфилда с весами равными скалярному произведению эталонов на предъявляемый образ:
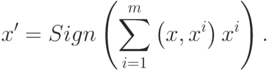 |
( 3) |
О сетях Хопфилда известно, что они способны запомнить и точно воспроизвести "порядка 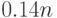 слабо скоррелированных образов". В этом высказывании содержится два ограничения:
слабо скоррелированных образов". В этом высказывании содержится два ограничения:
- число эталонов не превосходит
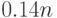 .
. - эталоны слабо скоррелированны.
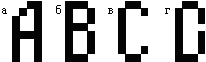
Наиболее существенным является второе ограничение, поскольку образы, которые сеть должна обрабатывать, часто очень похожи. Примером могут служить буквы латинского алфавита. При обучении сети Хопфилда распознаванию трех первых букв (см. рис. 8.1 а, б, в), при предъявлении на вход сети любого их эталонов в качестве ответа получается образ, приведенный на рис. 8.1 г.
В связи с такими примерами первый вопрос о качестве работы сети ассоциативной памяти звучит тривиально: будет ли сеть правильно обрабатывать сами эталонные образы (т.е. не искажает их)?