НОУ ИНТУИТ | Нейроинформатика. Лекция 8: Нейронные сети ассоциативной памяти

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 01.03.2007 | Доступ: свободный | Студентов: 1591 / 212 | Оценка: 4.58 / 4.39 | Длительность: 20:15:00

Тема: Искусственный интеллект и робототехника

Специальности: Программист

|

Вам нравится? Нравится 28 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Ортогональные сети

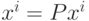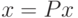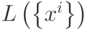Для обеспечения правильного воспроизведения эталонов достаточно потребовать, чтобы первое преобразование в (5) было таким, что x^i = Px^i . Очевидно, что если проектор является ортогональным, то это требование выполняется, поскольку x = Px при $x \in L\left( {\left\{ {x^i } \right\}} \right)$ , а $x^j \in L\left( {\left\{ {x^i } \right\}} \right)$ по определению множества $L\left( {\left\{ {x^i } \right\}} \right)$ .

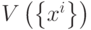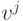Для обеспечения ортогональности проектора воспользуемся дуальным множеством векторов. Множество векторов $V\left( {\left\{ {x^i } \right\}} \right)$ называется дуальным к множеству векторов $\left\{ {x^i } \right\}$ если все вектора этого множества v^j удовлетворяют следующим требованиям:

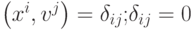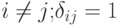$\left( {x^i ,v^j } \right) = \delta_{ij}{\rm{; }}\delta_{ij} = 0$ , при $i \ne j{\rm{; }}\delta_{ij} = 1$ при $i = j{\rm{;}}$
$v^j \in L\left( {\left\{ {x^i } \right\}} \right)$ .

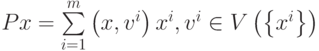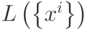Преобразование $Px = \sum\limits_{i = 1}^m {\left( {x,v^i } \right)x^i } ,{\rm{ }}v^i \in V\left( {\left\{ {x^i } \right\}} \right)$ является ортогональным проектором на линейное пространство $L\left( {\left\{ {x^i } \right\}} \right)$ .

Ортогональная сеть ассоциативной памяти преобразует образы по формуле

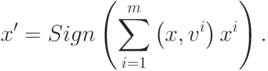$x' = Sign\left( {\sum\limits_{i = 1}^m {\left( {x,v^i } \right)x^i } } \right) .$

( 6)

Дуальное множество векторов существует тогда и только тогда, когда множество векторов $\left\{ {x^i } \right\}$ линейно независимо. Если множество эталонов $\left\{ {x^i } \right\}$ линейно зависимо, то исключим из него линейно зависимые образы и будем рассматривать полученное усеченное множество эталонов как основу для построения дуального множества и преобразования (6). Образы, исключенные из исходного множества эталонов, будут по-прежнему сохраняться сетью в исходном виде (преобразовываться в самих себя). Действительно, пусть эталон является линейно зависимым от остальных эталонов. Тогда его можно представить в виде

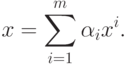
$x = \sum\limits_{i = 1}^m {\alpha_i x^i } .$

Подставив полученное выражение в преобразование (6) и учитывая свойства дуального множества получим:

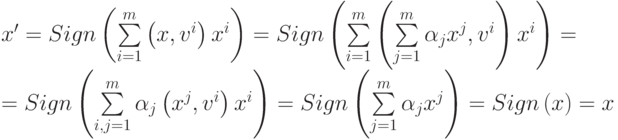$\begin{array}{l} x' = Sign\left( {\sum\limits_{i = 1}^m {\left( {x,v^i } \right)x^i } } \right) = Sign\left( {\sum\limits_{i = 1}^m {\left( {\sum\limits_{j = 1}^m {\alpha_j x^j } ,v^i } \right)x^i } } \right) = \\ = Sign\left( {\sum\limits_{i,j = 1}^m {\alpha_j \left( {x^j ,v^i } \right)x^i } } \right) = Sign\left( {\sum\limits_{j = 1}^m {\alpha_j x^j } } \right) = Sign\left( x \right) = x \\ \end{array}$

( 7)

Рассмотрим свойства сети (6) [8.2]. Во-первых, количество запоминаемых и точно воспроизводимых эталонов не зависит от степени их скоррелированности. Во-вторых, формально сеть способна работать без искажений при любом возможном числе эталонов (всего их может быть до 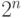2^n ). Однако, если число линейно независимых эталонов (т.е. ранг множества эталонов) равно , сеть становится прозрачной - какой бы образ не предъявили на ее вход, на выходе окажется тот же образ. Действительно, как было показано в (7), все образы, линейно зависимые от эталонов, преобразуются проективной частью преобразования (6) сами в себя. Значит, если в множестве эталонов есть линейно независимых, то любой образ можно представить в виде линейной комбинации эталонов (точнее линейно независимых эталонов), а проективная часть преобразования (6) в силу формулы (7) переводит любую линейную комбинацию эталонов в саму себя.

Если число линейно независимых эталонов меньше n , то сеть преобразует поступающий образ, отфильтровывая помехи, ортогональные всем эталонам.

Отметим, что результаты работы сетей (3) и (6) эквивалентны, если все эталоны попарно ортогональны.

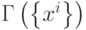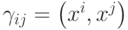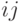Остановимся несколько подробнее на алгоритме вычисления дуального множества векторов. Обозначим через $\Gamma \left( {\left\{ {x^i } \right\}} \right)$ матрицу Грамма множества векторов $\left\{ {x^i } \right\}$ . Элементы матрицы Грамма имеют вид $\gamma_{ij} = \left( {x^i ,x^j } \right)$ ( -ый элемент матрицы Грамма равен скалярному произведению -го эталона на -ый). Известно, что векторы дуального множества можно записать в следующем виде:

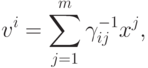$v^i = \sum\limits_{j = 1}^m {\gamma_{ij}^{ - 1} x^j } ,$

( 8)

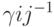где $\gamma {ij}^{ - 1}$ - элемент матрицы 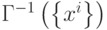$\Gamma^{ - 1} \left( {\left\{ {x^i } \right\}} \right)$ . Поскольку определитель матрицы Грамма равен нулю, если множество векторов линейно зависимо, то матрица, обратная к матрице Грамма, а следовательно и дуальное множество векторов существует только тогда, когда множество эталонов линейно независимо.

Для работы сети (6) необходимо хранить эталоны и матрицу 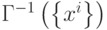$\Gamma^{ - 1} \left( {\left\{ {x^i } \right\}} \right)$ .

Рассмотрим процедуру добавления нового эталона к сети (6). Эта операция часто называется дообучением сети. Важным критерием оценки алгоритма формирования сети является соотношение вычислительных затрат на обучение и дообучение. Затраты на дообучение не должны зависеть от числа освоенных ранее эталонов.

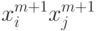Для сетей Хопфилда это, очевидно, выполняется - добавление еще одного эталона сводится к прибавлению к функции H одного слагаемого $\left( {x,x^{m + 1} } \right)^2$ , а модификация связей в сети - состоит в прибавлении к весу ij -й связи числа $x_i^{m + 1} x_j^{m + 1}$ - всего n^2 операций.

Дальше >>

Авторизоваться

Нейроинформатика

Нейронные сети ассоциативной памяти

Ортогональные сети

Вопросы и ответы