Нейронные сети ассоциативной памяти
Зависимость работы сети Хопфилда от степени скоррелированности образов можно легко продемонстрировать на следующем примере. Пусть даны три эталона  таких, что
таких, что
 |
( 4) |
Для любой координаты существует одна из четырех возможностей:

В первом случае при предъявлении сети  -го эталона в силу формулы (3) получаем
-го эталона в силу формулы (3) получаем  , так как все скалярные произведения положительны по условию (4). Аналогично получаем в четвертом случае
, так как все скалярные произведения положительны по условию (4). Аналогично получаем в четвертом случае  .
.
Во втором случае рассмотрим отдельно три варианта

так как скалярный квадрат любого образа равен  , а сумма двух любых скалярных произведений эталонов больше
, а сумма двух любых скалярных произведений эталонов больше  , по условию (4). Таким образом, независимо от предъявленного эталона получаем
, по условию (4). Таким образом, независимо от предъявленного эталона получаем  . Аналогично в третьем случае получаем
. Аналогично в третьем случае получаем  .
.
Окончательный вывод таков: если эталоны удовлетворяют условиям (4), то при предъявлении любого эталона на выходе всегда будет один образ. Этот образ может быть эталоном или "химерой", составленной, чаще всего, из узнаваемых фрагментов различных эталонов (примером "химеры" может служить образ, приведенный на рис. 8.1 г). Рассмотренный ранее пример с буквами детально иллюстрирует такую ситуацию.
Приведенные выше соображения позволяют сформулировать требование, детализирующие понятие "слабо скоррелированных образов". Для правильного распознавания всех эталонов достаточно (но не необходимо) потребовать, чтобы выполнялось следующее неравенство  . Более простое и наглядное, хотя и более сильное условие можно записать в виде
. Более простое и наглядное, хотя и более сильное условие можно записать в виде  . Из этих условий видно, что чем больше задано эталонов, тем более жесткие требования предъявляются к степени их скоррелированности, тем ближе они должны быть к ортогональным.
. Из этих условий видно, что чем больше задано эталонов, тем более жесткие требования предъявляются к степени их скоррелированности, тем ближе они должны быть к ортогональным.
Рассмотрим преобразование (3) как суперпозицию двух преобразований:
 |
( 5) |
Обозначим через  - линейное пространство, натянутое на множество эталонов. Тогда первое преобразование в (5) переводит векторы из
- линейное пространство, натянутое на множество эталонов. Тогда первое преобразование в (5) переводит векторы из 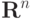 в
в 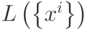 . Второе преобразование в (5) переводит результат первого преобразования
. Второе преобразование в (5) переводит результат первого преобразования 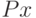 в одну из вершин гиперкуба образов. Легко показать, что второе преобразование в (5) переводит точку
в одну из вершин гиперкуба образов. Легко показать, что второе преобразование в (5) переводит точку 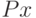 в ближайшую вершину гиперкуба. Действительно, пусть
в ближайшую вершину гиперкуба. Действительно, пусть  и
и  две различные вершины гиперкуба такие, что
две различные вершины гиперкуба такие, что  - ближайшая к
- ближайшая к 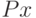 , а
, а  . Из того, что
. Из того, что  и
и  различны следует, что существует множество индексов,
в которых координаты векторов
различны следует, что существует множество индексов,
в которых координаты векторов  и
и  различны. Обозначим это множество через
различны. Обозначим это множество через  . Из второго преобразования в (5) и того, что
. Из второго преобразования в (5) и того, что  , следует, что знаки координат вектора
, следует, что знаки координат вектора 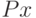 всегда совпадают со знаками соответствующих координат вектора
всегда совпадают со знаками соответствующих координат вектора  . Учитывая различие знаков
. Учитывая различие знаков  -х координат векторов
-х координат векторов  и
и 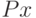 при
при  можно записать
можно записать  . Совпадение знаков
. Совпадение знаков  -х координат векторов
-х координат векторов  и
и 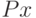 при
при  позволяет записать следующее неравенство
позволяет записать следующее неравенство  . Сравним расстояния от вершин
. Сравним расстояния от вершин  и
и  до точки
до точки 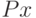

Полученное неравенство  противоречит тому, что
противоречит тому, что  - ближайшая к
- ближайшая к 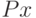 . Таким образом доказано, что второе преобразование в (5) переводит точку
. Таким образом доказано, что второе преобразование в (5) переводит точку 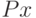 в ближайшую вершину гиперкуба образов.
в ближайшую вершину гиперкуба образов.
