Нейронные сети ассоциативной памяти
Сети для инвариантной обработки изображений
Для того, чтобы при обработке переводить визуальные образов, отличающиеся только положением в рамке изображения, в один эталон, применяется следующий прием [8.7]. Преобразуем исходное изображение в некоторый вектор величин, не изменяющихся при сдвиге (вектор инвариантов). Простейший набор инвариантов дают автокорреляторы - скалярные произведения образа на сдвинутый образ, рассматриваемые как функции вектора сдвига.
В качестве примера рассмотрим вычисление сдвигового автокоррелятора для черно-белых изображений. Пусть дан двумерный образ  размером
размером 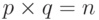 . Обозначим точки образа как
. Обозначим точки образа как 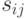 . Элементами автокоррелятора
. Элементами автокоррелятора 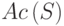 будут величины
будут величины

 при выполнении любого из неравенств
при выполнении любого из неравенств 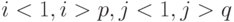 . Легко проверить, что автокорреляторы любых двух образов, отличающихся только расположением в рамке, совпадают. Отметим, что
. Легко проверить, что автокорреляторы любых двух образов, отличающихся только расположением в рамке, совпадают. Отметим, что 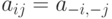 при всех
при всех  ,
и
,
и 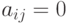 при выполнении любого из неравенств
при выполнении любого из неравенств 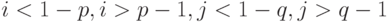 . Таким образом, можно считать, что размер автокоррелятора равен
. Таким образом, можно считать, что размер автокоррелятора равен 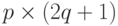 .
.Автокорреляторная сеть имеет вид
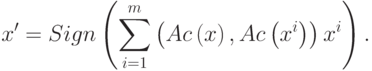 |
( 11) |
Сеть (11) позволяет обрабатывать различные визуальные образы, отличающиеся только положением в рамке, как один образ.
Подводя итоги, можно сказать, что все сети ассоциативной памяти типа (2) можно получить, комбинируя следующие преобразования:
- Произвольное преобразование. Например, переход к автокорреляторам, позволяющий объединять в один выходной образ все образы, отличающиеся только положением в рамке.
- Тензорное преобразование, позволяющее сильно увеличить способность сети запоминать и точно воспроизводить эталоны.
- Переход к ортогональному проектору, снимающий зависимость надежности работы сети от степени скоррелированности образов.
Наиболее сложная сеть будет иметь вид:
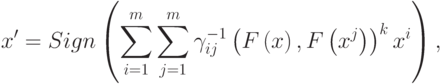 |
( 12) |
где 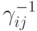 - элементы матрицы, обратной матрице Грамма системы векторов
- элементы матрицы, обратной матрице Грамма системы векторов
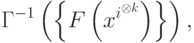
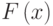 - произвольное преобразование.
- произвольное преобразование.Численный эксперимент
Работа ортогональных тензорных сетей при наличии помех сравнивалась с возможностями линейных кодов, исправляющих ошибки. Линейным кодом, исправляющим k ошибок, называется линейное подпространство в n -мерном пространстве над GF2, все вектора которого удалены друг от друга не менее чем на 2k+1 (см., например, [8.8]). Линейный код называется совершенным, если для любого вектора n -мерного пространства существует кодовый вектор, удаленный от данного не более, чем на k. Тензорной сети в качестве эталонов подавались все кодовые векторы избранного для сравнения кода. Численные эксперименты с совершенными кодами показали, что тензорная сеть минимально необходимой валентности правильно декодирует все векторы. Для несовершенных кодов картина оказалась хуже - среди устойчивых образов тензорной сети появились "химеры" - векторы, не принадлежащие множеству эталонов.
В случае n=10, k=1 (см. табл. 8.1 2 и 3, строка 1) при валентностях 3 и 5 тензорная сеть работала как единичный оператор - все входные вектора передавались на выход сети без изменений. Однако уже при валентности 7 число химер резко сократилось и сеть правильно декодировала более 60% сигналов. При этом были правильно декодированы все векторы, удаленные от ближайшего эталона на расстояние 2, а часть векторов, удаленных от ближайшего эталона на расстояние 1, остались химерами. В случае n=10, k=2 (см. табл. 8.1 2 и 3, строки 3, 4, 5) наблюдалось уменьшение числа химер с ростом валентности, однако часть химер, удаленных от ближайшего эталона на расстояние 2 сохранялась. Сеть правильно декодировала более 50% сигналов. Таким образом при малых размерностях и кодах, далеких от совершенных, тензорная сеть работает довольно плохо. Однако, уже при n=15, k=3 и валентности, большей 3 (см. табл. 8.1 2 и 3, строки 6, 7), сеть правильно декодировала все сигналы с тремя ошибками. В большинстве экспериментов число эталонов было больше числа нейронов.
Подводя итог, можно сказать, что качество работы сети возрастает с ростом размерности пространства и валентности и по эффективности устранения ошибок сеть приближается к коду, гарантированно исправляющему ошибки.
Работа выполнена при поддержке Красноярского краевого фонда науки, грант 6F0124.
