База знаний Wolfram|Alpha

Если функцию Circle заменить функцией Disk, то эллипс она вернет окрашенный, а вместо дуги эллипса будет построен его сектор.

Скругленный прямоугольник красного цвета можно построить с помощью запроса

Graphics[{Red, Rectangle[{0, 0}, {2, 1}, 
RoundingRadius -> 0.3]}]

Кривые Безье и B-сплайны

В ответ на запрос

bezier curve или b spline

система Wolfram|Alpha выдает только определение кривой Безье или B-сплайна, соответственно. Примеры данных кривых система показывает в результате запросов о функциях языка Wolfram вида

wolfram language symbol BezierCurve

(аналогично для функции BSplineCurve).

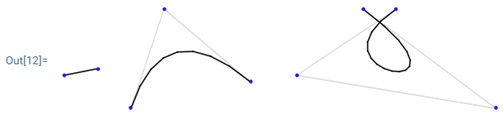
Пример 12. Рассмотрим примеры построения в облаке Wolfram кривых Безье первого, второго и третьего порядка по двум, трем и четырем точкам, соответственно:

 In[9]:= two = {{0, 0}, {0.5, 0.1}}; 
three = {{1, -0.5}, {1.5, 1}, {2.8, -0.1}};
four = {{4.5, 1}, {6.5, -0.5}, {3.5, 0}, {5, 1}};
Graphics[{LightGray, Line[three], Line[four], 
Black, BezierCurve[two], BezierCurve[three], 
BezierCurve[four], Blue, Point[two], 
Point[three], Point[four]}]

Результат показан на

рис. 7.8

Рис. 7.8. Кривые Безье первого, второго и третьего порядка

Если число точек в списке превышает 4, то они разбиваются на группы по 4 точки, так что последняя точка группы является первой точкой следующей группы, и для каждой группы строятся кривые Безье третьего порядка. Если в последней группе точек оказывается меньше четырех, т. е. она содержит 2 или 3 точки, то для нее строится кривая Безье первого или второго порядка, соответственно.

Ниже показан пример построения кривой по 9 точкам. Для точек с индексами 0 - 3 и 3 - 6 строятся кривые Безье третьего порядка, а для точек с индексами 6 - 8 - кривая Безье второго порядка

рис. 7.9

 In[13]:= p = {{0, 0}, {1, 1}, {2, -1}, {5, 2}, {7, -1}, 
{3, -1}, {6, 1}, {8, 2}, {9, 0}};
Graphics[{LightGray, Line[p], Black, 
BezierCurve[p], Blue, Point[p]}

Рис. 7.9. Кривая, составленная из трех кривых Безье

Пример 13. B-сплайн по тем же 9 точкам, что и в примере 12, можно построить следующим образом

рис. 7.10

 In[15]:= Graphics[{LightGray, Line[p], Black, 
BSplineCurve[p], Blue, Point[p]}

Рис. 7.10. B-сплайн, построенный по 9 точкам

Аналогичным образом кривые Безье и B-сплайны, а также другие графические примитивы строятся в трехмерном пространстве с помощью функции Graphics3D. Для точек в этом случае должны указываться по 3 координаты.

Фракталы

Примеры разного рода фракталов в системе Wolfram|Alpha предлагаются по запросу fractal или fractals.

В языке Wolfram также имеется большое количество функций для построения различных фракталов.

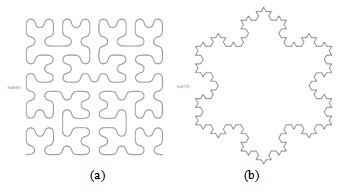
Пример 14. Ниже приведен пример построения кривой Гильберта (4 итерации), в которой ломаная заменена B-сплайном

рис. 7.11 (a)

 In[16]:= 	Graphics[{HilbertCurve[4]/.Line->BSplineCurve}]

Снежинку Коха

рис. 7.11 (b)

In[17]:= Graphics[GeometricTransformation[KochCurve[3], 
{RotationTransform[Pi, {1/2, 0}], 
 RotationTransform[-Pi/3, {1, 0}], 
 RotationTransform[Pi/3, {0, 0}]}]] 

Рис. 7.11. Приближение (a) кривой Гильберта; (b) снежинки Коха

Изображения. Звуки

В системе Wolfram|Alpha изображениями сопровождается большое количество разнообразных запросов. Например, по запросу Eiffel Tower приводятся изображения как самой Эйфелевой башни, так и ее местоположения. Кроме этого, сообщается информация об этой башне.

В ответ на запросы о преобразованиях изображений возвращаются функции языка Wolfram.

В облаке Wolfram изображение можно вставить непосредственно из буфера (используя команды копировать + вставить) и присвоить его переменной (в данном случае myimage), как обычный символ

рис. 7.12

Рис. 7.12. Изображение в облаке Wolfram

Пример 15. Ниже приведены примеры запросов, которые выполняют геометрические преобразования - отражение и поворот, заменяют цвета изображения на дополнительные в модели RGB, а также создают эффект "размытия" изображения

рис 7.13 (a-d)

 In[2]:=ImageReflect[myimage, Left]
ImageRotate[myimage, Right] 
ColorNegate[myimage]
Blur[myimage]

Рис. 7.13. Операции (a) отражения; (b) поворота; (c) инверсии; (d) размытия

Систему Wolfram|Alpha можно использовать для настройки музыкальных инструментов. Для того чтобы услышать звучание ноты или последовательности нот, достаточно ввести их название в строку поиска, например, в виде F#, C#, A#

ответ система Wolfram|Alpha покажет изображение нот на нотном стане

рис. 7.14

Рис. 7.14. Изображение нот фа-диез, до-диез, ля-диез на нотном стане

Звучание можно прослушать с помощью кнопки Play Sound.

Пример 16. Ниже приведены примеры трех запросов в облаке Wolfram, в результате ответа на которые появляется проигрыватель для прослушивания звучания нот. Ноты можно обозначать как буквами, так и цифрами: 0 соответствует ноте до первой октавы, 12 - ноте до второй октавы.

В результате первого запроса можно прослушать гамму до мажор и аккорд до-ми-соль. Второй запрос - ноты ре, фа-диез, ля, ре и аккорд, третий - хроматическая гамма от 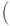ступени

рис. 7.15

In[1]:= Sound[{SoundNote["C"], SoundNote["D"],
 SoundNote["E"], SoundNote["F"], SoundNote["G"],
 SoundNote["A"], SoundNote["B" SoundNote[12],
 SoundNote[{"C", "E", "G"}]}]
Sound[{SoundNote[2], SoundNote[6], SoundNote[9],
 SoundNote[14], SoundNote[{2, 6, 9, 14}]}]
Sound[Table[SoundNote[n],{n, 0, 12}]]

Рис. 7.15. (a) До мажор; (b) ре мажор; (c) хроматическая гамма

Запросы о логических преобразованиях

Рассмотрим запросы, связанные с преобразованиями логических выражений, электронными логическими схемами, битовыми операциями, играми и клеточными автоматами.

Логические выражения

Для логических операций в системе Wolfram|Alpha используются следующие обозначения:

• дизъюнкция: or или ||;
• конъюнкция: and или &&;
• отрицание: not или !;
• импликация: implies или =>;
• эквиваленция: equivalent или <=>;
• строгая дизъюнкция:xor;
• штрих Шеффера: nand;
• стрелка Пирса: nor;
• отрицание строгой дизъюнкции: xnor;

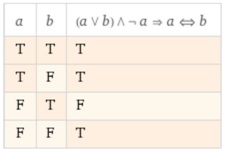
Пример 17. Построить таблицу истинности логического выражения можно с помощью запроса вида

truth table ((a || b) && !a) => (a <=> b)

Таблица истинности показана на рис. 7.16. Выражение предварительно не упрощается.

Рис. 7.16. Таблица истинности для выражения...

Пример 18. Упростить логическое выражение в системе Wolfram|Alpha можно, например, следующим образом:

simplify ((a or not b) and c) xnor ((a implies not c) nor a)

Результат имеет вид: .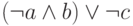

Кроме упрощенного выражения, приводится его ДНФ, КНФ и другие формы его представления через подмножество логических операций. Для исходного выражения также приводится таблица истинности, схема логической функции и клеточный автомат с правилом, которое представляет эта функция, если она имеет 3 аргумента.

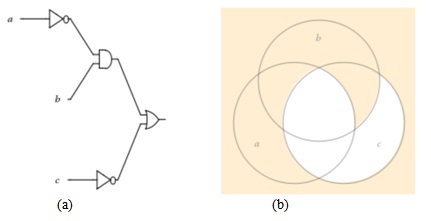
Рассмотрим результаты запроса для упрощенного выражения (not a and b) or not c.

Электронная логическая схема и диаграмма Венна, или Эйлера-Венна приведены на

рис. 7.17 (a-b)

Рис. 7.17. (a) Электронная логическая схема; (b) диаграмма Эйлера-Венна

На

рис. 7.18

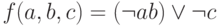Начальное состояние соответствует верхнему ряду поля.

Рис. 7.18. Клеточный автомат для правила...

На языке Wolfram таблицу истинности для рассматриваемого выражения можно построить следующим образом:

In[1]:= 	BooleanTable[{a, b, c, Or[And[Not[a], b], Not[c]]},
{a, b, c}]//TableForm
Out[1]//TableForm= 
True	True 	True	False
True	True	False	True
True	False	True	False
True	False	False	True
False	True	True	True
False	True	False	True
False	False	True	False
False	False	False	True