База знаний Wolfram|Alpha

Вместо изображения с именем сущности можно, как и выше, использовать функцию Entity. Кроме этого, можно запрашивать информацию не только о конкретных свойствах, но и о наборах свойств:

Entity["FamousMathGame", "Nim"][{ "Diagram", "Classes"}]

Для того чтобы получить информацию обо всех типах сущностей, которые имеются в базе знаний, следует ввести в строку поиска облака Wolfram запрос

Entity Types

В результате появится информация о большом количестве типов сущностей, классифицированных по областям знаний. В частности, сведения о функциях, с помощью которых можно формулировать запросы о сущностях, принадлежащих типу "FamousMathGame", находятся в разделе Mathematical & Computational Entities.

Элементарные клеточные автоматы

Общие сведения о клеточных автоматах, а также их примеры система Wolfram|Alpha приводит в ответ на запрос:

cellular automaton

Пример 22. Информацию об элементарном клеточном автомате, который соответствует конкретному правилу, например 86, система Wolfram|Alpha возвращает в ответ на запрос

cellular automaton rule 86

В частности, приводится логическая и алгебраическая форма правила 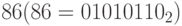. Эти формы, соответственно, имеют вид:

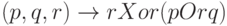
и

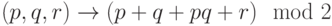
Рассмотрим примеры запросов в облаке Wolfram.

Представить правило 86 в виде преобразований клеток можно следующим образом:

In[1]:= 	RulePlot[CellularAutomaton[86]]

Out[1]=

Клетка черного цвета соответствует 1, белого - 0.

Состояния клеточного автомата в моменты времени 0 - 10 программа возвращает в результате запроса вида

рис. 7.20

In[2]:= 	RulePlot[CellularAutomaton[86], {{1}, 0}, 10,
Mesh -> All, ImageSize -> Full]

В начальном состоянии центральная клетка имеет черный цвет. Слева и справа от нее расположены клетки белого цвета, число которых равно числу шагов. На

рис. 7.20

Рис. 7.20. Состояния 0 - 10 клеточного автомата для правила 86

Первые 50 состояний поля с аналогичным начальным состоянием можно также увидеть с помощью запроса

ArrayPlot[CellularAutomaton[86, {{1}, 0}, 50]]

В результате следующего запроса возвращаются первые 2 состояния автомата для начального состояния, описываемого явным образом:

 In[3]:= 	CellularAutomaton[86, {1,0,0,0,1,0,0}, 2]
 Out[3]= 	{{1, 0, 0, 0, 1, 0, 0}, {1, 1, 0, 1, 1, 1, 1}, {0, 1, 0, 0, 0, 0, 0}}
 In[4]:= 	CellularAutomaton[86, {1,0,0,0,1,0,0}, 2]//Grid

Правила могут описываться с помощью логических или алгебраических функций (см. выше), например в виде

 In[5]:= 	CellularAutomaton[{{p_, q_, r_} -> Xor[r, Or[p, q]]},
{{True}, False}, 2]
 Out[5]= 	{{False, False, True, False, False}, {False, True, True, True, False},
{True, False, False, True, True}}
 In[6]:= 	ArrayPlot[Boole[%]]

Out[6]=

Игра "Жизнь"

Информацию об игре Джона Конвея "Жизнь" и примеры некоторых начальных состояний для этой игры можно получить в системе Wolfram|Alpha с помощью запроса

Conway's Game of Life

Пример 21. Рассмотрим пример построения клеточного поля со случайным набором живых клеток в начальном состоянии в облаке Wolfram.

Случайная расстановка живых клеток строится с помощью функции RandomInteger. Например, поле 5 * 5 может иметь вид:

 In[1]:= 	RandomInteger[1, {5, 5}]//Grid

Следующий пример реализации игры "Жизнь" приводится в документации языка Wolfram (поле сокращено до размера 20 * 20):

In[2]:= 	gameOfLife = {224, {2, {{2, 2, 2}, {2, 1, 2}, 
{2,, 2}}}, {1, 1}};
board = RandomInteger[1, {20, 20}]; 
Dynamic[ArrayPlot[board =
Last[CellularAutomaton[gameOfLife, board, 
{{0, 1}}]]]]

В первой строке кода описываются правила игры "Жизнь"; они присваиваются переменной gameOfLife. Во второй строке переменной board присваивается значение начальной конфигурации живых клеток поля; эта конфигурация задается случайным образом. Третья строка описывает динамическое отображение состояний поля, при этом в переменной board запоминается последнее состояние, которое затем преобразуется по правилам игры.

Состояния поля автоматически обновляются. На

рис. 7.21

Рис. 7.21. Состояния клеточного поля в игре "Жизнь"

Состояние поля на конкретном шаге можно получить следующим образом:

 In[5]:= 	board1 = {{0,0,1,0,0}, {1,0,1,0,0}, 
{0,1,1,0,0}, {0,0,0,0,0}, {0,0,0,0,0}};
Grid[board1]

In[7]:= 	ArrayPlot[CellularAutomaton[gameOfLife, board1,
{{{4}}}]]

Переменная board1 хранит начальное состояние поля (см. Out[6]). Программа вычисляет состояние поля на шаге 4.