Кодирование чисел и текста
Если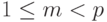 
, то такое представление числа x называется нормализованным, или нормальным, а если 
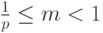, то денормализованным, или субнормальным.
Число, представленное в нормальной или субнормальной форме, называется, соответственно, нормализованным или субнормальным (денормализованным).
В экспоненциальной форме числа представляются в формате m+eq, m-eq, - m+eq или - m-eq, где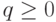 
. Если 
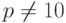, то числа p и q могут оставаться в десятичном виде.
Пример 9. Представим числа в нормализованном виде:
- 43000 = 4,3+e4; 0,00003 = 3-e05; - 1 = - 1+e0 (p = 10);
-
; 
; -
.
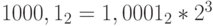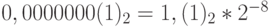Пример 10. Перейдем от экспоненциального формата к представлению в p-ичном виде:
- 2,3456701+e10 = 23456701000; 3,14151-e02 = 0,0314151;
-
; 
; -
.
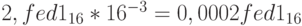Пример 11. Представим десятичное число 22,3 в денормализованном виде. Имеем: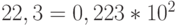 
. Поэтому мантисса числа 22,3 в субнормальной форме равна 0,223, а порядок равен 2.
В двоичной системе счисления
Отметим, что целая часть мантиссы ненулевого двоичного нормализованного числа всегда равна 1. Соответственно, первым знаком после запятой ненулевого двоичного субнормального числа является 1.
Операции с нормализованными числами
Рассмотрим арифметические операции с нормализованными числами. Операции сложения и вычитания производятся с помощью операции выравнивания - приведения к большему порядку. Для операций умножения и деления такого выравнивания не требуется.
Пусть 
и 
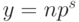- нормализованные числа, где m, n, q, s, - целые, 
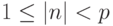для 
, 
для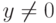 
.
Тогда
;
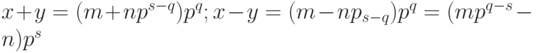}, если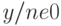 
.
После выполнения арифметической операции производится операция приведения результата к нормальной форме. Аналогичным образом выполняются операции с субнормальными числами.
Пример 12. Для десятичных чисел имеем:
-
; -
; -
; -
.
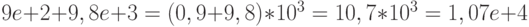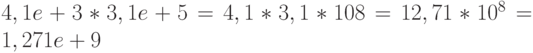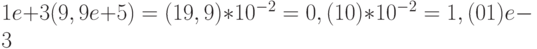Пример 13. Для двоичных чисел аналогичным образом получаем:
-
; -
; -
; -
.
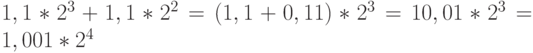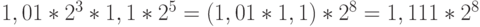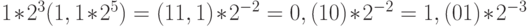Если число разрядов, которые используются для хранения чисел, ограничено, то при выполнении арифметических операций могут возникать ошибки из-за необходимости округления чисел.
Пусть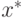 
- (приближенное) представление ненулевого числа x. Величина 
называется абсолютной погрешностью представления, а величина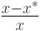 
- его относительной погрешностью.
Пример 14. Пусть x = 3,14159 и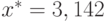 
. Тогда абсолютная и относительная погрешности равны, соответственно, 0,00041 и 
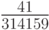, или 0,000130507... Из значения относительной погрешности следует, что верными в представлении являются 3 значащие цифры, т. е. 3,14. Относительная погрешность не изменится для чисел x = 314,159 и 
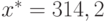, а абсолютная погрешность увеличится в 100 раз.
Представление ненулевых конечных нормализованных чисел
Рассмотрим методы представления действительных чисел в типах данных short (с половинной точностью), float (с одинарной точностью), double (с двойной точностью) и long (с двойной расширенной точностью). Ниже приведена таблица числа разрядов, которые отводятся на хранение знака, порядка и дробной части мантиссы в этих типах данных (табл. 2.3).
| Тип | Знак | Порядок | Мантисса | Общее число разрядов |
|---|---|---|---|---|
| short | 1 | 5 | 10 | 16 |
| float | 1 | 8 | 23 | 32 |
| double | 1 | 11 | 52 | 64 |
| long | 1 | 15 | 64 | 80 |
Пусть ненулевое действительное число x в нормализованной двоичной форме имеет вид 
, где
f - дробная часть мантиссы и q - целое число.
В старшем разряде типа данных хранится число s.
В разрядах, предназначенных для хранения порядка, хранится двоичное представление смещенного порядка, который обозначается e (от англ. exponent) и который в десятичной форме имеет вид:
e = bias + q,
где через bias обозначается величина смещения. Смещение используется для того, чтобы величина e была неотрицательной. Пусть k - число разрядов, которые используются для хранения порядка. Тогда
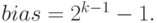
Таким образом, для типов данных short, float, double и long значение bias соответственно равно 15, 127, 1023 и 16383 (см. табл. 2.3).