Кодирование чисел и текста

Операции сложения и вычитания целых чисел

Пусть x и y - два неотрицательных целых числа. В компьютерных вычислениях разность y - x заменяется суммой прямого кода числа y и дополнительного кода числа (- x). Пусть сначала . Тогда

Коэффициент при 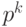выйдет за границы k разрядов, поэтому он отбрасывается (напомним, что числа рассматриваются как остатки от деления на 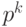). Оставшийся код является прямым кодом разности y - x.

Пусть теперь x > y. Тогда y - x < 0. Имеем:

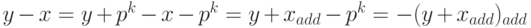
Таким образом,

Следовательно, если при вычислениях разность получается отрицательной (код начинается с p - 1), то величина y - x находится как дополнительный код полученного результата, умноженный на (- 1).

Аналогично,

Таким образом,

Пример 6. Найдем результаты операций сложения и вычитания

1. 5 - 3; 5 + 3;
2. 3 - 5; - 3 - 5

в двоичных кодах при кодировании в 1 байте.

Имеем: ; .

1. Вычислим и . Для этого найдем и . Имеем:

   

   
   

   Старший разряд полученных чисел равен 0, поэтому они представляют прямой код результатов, которые соответственно имеют вид:

   

2. Найдем 3 - 5 и - 3 - 5. Для этого вычислим и :

   

   
   

   Старший разряд обоих полученных чисел равен 1. Поэтому они представляют отрицательные числа, и в обоих случаях следует найти дополнительный код. Имеем:

   00000001 + 1 = 00000010;
   00000111 + 1 = 00001000.

   Дополнительный код представляет собой прямой код абсолютной величины результата. Следовательно, 3 - 5 = - 2 и - 3 - 5 = - 8.

Пример 7. Найдем разность 128 - 589, заменив операцию вычитания операцией сложения. Для десятичного кодирования в данном случае достаточно использовать 4 разряда (пример 4).

Прямой код числа 589 имеет вид: 0589. Поэтому дополнительный код числа (- 589) выглядит следующим образом: 9410 + 1 = 9411.

Найдем сумму прямого кода первого числа и дополнительного кода второго: 0128 + 9411 = 9539. Старший разряд полученного числа равен 9, поэтому оно представляет отрицательное число, и необходимо найти дополнительный код: 0460 + 1 = 0461. Таким образом, 128 - 589 = - 461.

Аналогичным образом вычислим сумму (- 128 - 589) с помощью сложения дополнительных кодов. Имеем: 9411 + 9872 =1 19283. Следовательно, - 128 - 589 = - 717.

При выполнении арифметических операций в k разрядах могут возникать ошибки.

Пример 8. Найдем сумму 58 + 96 при двоичном кодировании в 1 байте для типа данных целых чисел со знаком. Имеем: . Далее, 00111010 + 01100000 = 10011010.

Старший разряд полученного числа равен 1. Поэтому для полученного числа будет найден дополнительный код: 01100101 + 1 = 01100110. Далее, , и результат будет иметь вид: 58 + 96 = - 102. Причина заключается в том, что слагаемые находятся внутри диапазона чисел типа данных (табл. 2.2), а сумма - вне, так что фактически находится число 58 + 96 - 256 = - 102. В данном случае для корректного выполнения арифметических операций следует перейти к типу данных, который содержит большее число разрядов.

Кодирование действительных чисел

Действительные числа в электронных вычислительных устройствах могут иметь представление в двух форматах - с фиксированной запятой (или точкой), где для хранения дробной части используется фиксированное число разрядов, и с плавающей запятой (точкой). Ниже рассматриваются методы кодирования действительных чисел в формате с плавающей запятой (точкой) в соответствии со стандартом IEEE 754 (ред. 2019), который был разработан Институтом инженеров по электротехнике и радиоэлектронике (Institute of Electrical and Electronic Engineers).

Представление числа в нормализованном виде

Пусть p - основание системы счисления, где p - целое, p > 1.

Экспоненциальной формой представления ненулевого числа x называется его представление в виде

где s = 0 для положительных чисел, s = 1 для отрицательных чисел, m > 0 и q - целое число. Число m называется мантиссой числа x, а число q - порядком. Для числа 0 мантисса и порядок полагаются равными 0, так что 0 представляется в виде .