Введение в информатику
[+]
Российский государственный гуманитарный университет
Опубликован: 13.07.2022 | Доступ: свободный | Студентов: 350 / 39 | Длительность: 11:54:00
Темы: Программирование, Образование, Школа
Специальности: Программист
Лекция 1:

Представление чисел в системах счисления
A
|
версия для печати
Лекция 1: 1234 || Лекция 2 >

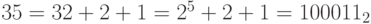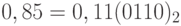Пример 8. Найдем представление числа 35,85 в двоичной системе счисления. Имеем: 35 = 32 + 2 + 1 = 2^5 + 2 + 1 = 100011_2. Для преобразования числа 0,85 будем последовательно удваивать дробные части результатов, начиная с этого числа: 1,7; 1,4; 0,8; 1,6; 1,2; 0,4; 0,8, ... Таким образом, 0,85 = 0,11(0110)_2.

Следовательно,

35,85 = 100011,11(0110)_2.
Преобразование p-ичных чисел в десятичные

Пусть для неотрицательного действительного числа x верно разложение (1). Рассмотрим некоторые способы преобразования числа x из системы счисления с основанием p в десятичную систему счисления.

Первый способ заключается в непосредственном применении формулы (1) (пример 4). Для вычислений можно использовать таблицы, в которых записывается соответствие между коэффициентами и степенями p в указанном разложении.

Пример 9. Найдем десятичное представление числа 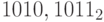1010,1011_2 с помощью таблицы 1.2.

Таблица 1.2. Соответствие коэффициентов степеням 2
1 0 1 0 1 0 1 1
8 4 2 1 1/2 1/4 1/8 1/16

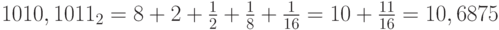Имеем: 1010,1011_2=8+2+\frac{1}{2}+\frac{1}{8}+\frac{1}{16}=10+\frac{11}{16}=10,6875.

Второй способ называется схемой Горнера. Он обычно используется в компьютерных программах, так как позволяет существенно упростить вычисления. Заметим, что

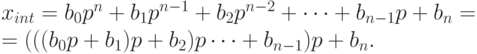
x_{int}= b_0p^n + b_1p^{n - 1} + b_2p^{n - 2} + \dots + b_{n - 1}p + b_n = \\ = (((b_0p + b_1)p + b_2)p \dots + b_{n - 1})p + b_n.

Утверждение 1. Положим

z_0 = b_0, z_j = z_{j - 1}p + b_j, ( 3)

для j = 1, 2, ..., n. Тогда 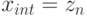x_{int} = z_n.

Доказательство. Для доказательства применим метод математической индукции. Используем индукцию по n.

Рассмотрим случай n = 1. Тогда 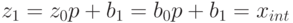z_1 = z_0p + b_1 = b_0p + b_1 = x_{int}. Следовательно, при n = 1 утверждение верно.

Предположим, что утверждение верно для 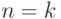n = k, т. е. что верно следующее соотношение:

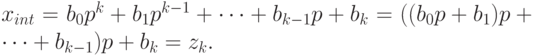
x_{int}= b_0p^k + b_1p^{k - 1} + \dots + b_{k - 1}p + b_k = ((b_0p + b_1)p + \dots + b_{k - 1})p + b_k = z_k.

Пусть теперь n = k + 1. Тогда, по предположению индукции,

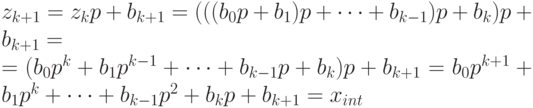
z_{k + 1}= z_kp + b_{k + 1} = (((b_0p + b_1)p + \dots + b_{k - 1})p + b_k)p + b_{k + 1} =\\ = (b_0p^k + b_1p^{k - 1} + \dots + b_{k - 1}p + b_k)p + b_{k + 1} = b_0p^{k + 1} + b_1p^k + \dots + b_{k - 1}p^2 + b_kp + b_{k + 1} = x_{int}

Следовательно, утверждение верно для 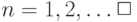n = 1, 2, \dots \Box

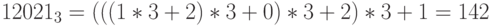Пример 10. Найдем десятичное представление числа 12021_3. Имеем: 12021_3 = (((1 * 3 + 2) * 3 + 0) * 3 + 2) * 3 + 1 = 142 ( табл. 1.3).

Таблица 1.3. Преобразование в десятичную систему счисления целого числа, p = 3
b_j 1 2 0 2 1
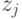z_j 1 5 15 47 142

Если дробная часть числа x содержит k знаков после запятой, то для нее выполняется аналогичное соотношение:

x_{fract}= b_{n + 1}p^{- 1} + b_{n + 2}p^{- 2} + \dots + b_{n + k}p^{ - k} =\\ = p^{- k}(b_{n + 1}p^{k - 1} + b_{n + 2}p^{k - 2} + \dots + b_{n + k}) =\\ = p^{- k}(((b_{n + 1}p + b_{n + 2})p + \dots + b_{n + k - 1})p + b_{n + k}).

Представление дробной части можно кратко записать в виде

x_{fract} = p^{ - k} * b_{n + 1}b_{n + 2} \dots b_{n + k p}.

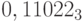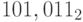Пример 11. Используя схему Горнера, найдем десятичное представление чисел 0,11022_3 и 101,011_2. Имеем:

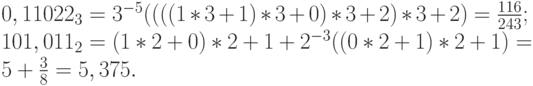
0,11022_3 = 3^{-5}((((1 * 3 + 1) * 3 + 0) * 3 + 2) * 3 + 2) =\frac{116}{243};\\ 101,011_2 = (1 * 2 + 0) * 2 + 1 + 2^{- 3}((0 * 2 + 1) * 2 + 1) = 5 +\frac{3}{8} = 5,375.

Результаты вспомогательных вычислений для числа 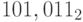101,011_2 приведены в табл. 1.4.

Таблица 1.4. Преобразование в десятичную систему счисления, p = 2
b_j 1 0 1 0 1 1
z_j 1 2 5 0 1 3

Пусть теперь дробная часть числа обладает периодом длины s и выглядит следующим образом:

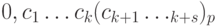
0, c_1\dots c_k(c_{k+1}\dotsc_{k+s})_p

где s > 0 и 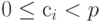0 \le с_i < p, для i = 1, ..., k, k + 1, ..., k + s. Обозначим через a и b целые десятичные числа, представление которых в системе счисления с основанием p имеет вид:

a = c_1\dotsc_{k p},\\ b = c_{k + 1}\dotsc_{k + s p}.

Утверждение 2. Является верным равенство:

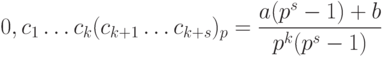0,c_1 \dots c_k(c_{k+1}\dots c_{k+s})_p=\frac{a(p^s-1)+b}{p^k(p^s-1)} ( 4)

Доказательство. Для доказательства используем разложение (1) и формулу суммы бесконечно убывающей геометрической прогрессии. Имеем:

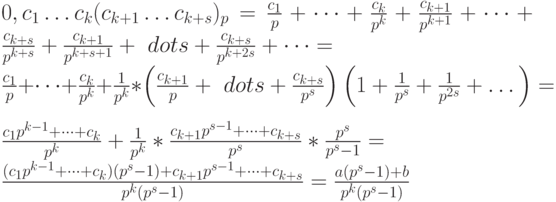
0,c_1\dots c_k(c_{k+1}\dots c_{k+s})_p=\frac{c_1}{p}+\dots+\frac{c_k}{p^k}+\frac{c_{k+1}}{p^{k+1}}+\dots+\frac{c_{k+s}}{p^{k+s}}+\frac{c_{k+1}}{p^{k+s+1}}+\ dots+\frac{c_{k+s}}{p^{k+2s}}+\dots=\\ \frac{c_1}{p}+\dots+\frac{c_k}{p^k}+\frac{1}{p^k}*\left( \frac{c_{k+1}}{p}+\ dots+\frac{c_{k+s}}{p^s}\right) \left(1+\frac{1}{p^s}+\frac{1}{p^{2s}}+\dots \right)=\\ \frac{c_1p^{k-1}+\dots+c_k}{p^k}+\frac{1}{p^k}*\frac{c_{k+1}p^{s-1}+\dots+c_{k+s}}{p^s}*\frac{p^s}{p^s-1}=\\ \frac{(c_1p^{k-1}+\dots+c_k)(p^s-1)+c_{k+1}p^{s-1}+\dots+c_{k+s}}{p^k(p^s-1)}=\frac{a(p^s-1)+b}{p^k(p^s-1)}

Пример 12. Используя формулу (4), представим число в виде рациональной дроби:

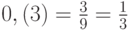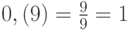  1. 0,(3)=\frac39=\frac13; 0,(9)=\frac99=1 (здесь s = 1, k = 0 и a = 0);
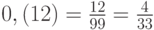  2. 0,(12)=\frac{12}{99}=\frac{4}{33};
  3. 0,12(345)=\farc{12-999+345}{100*999}=\frac{4111}{33300};
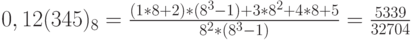  4. 0,12(345)_8=\frac{(1*8+2)*(8^3-1)+3*8^2+4*8+5}{8^2*(8^3-1)}=\frac{5339}{32704};
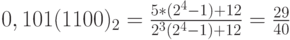  5. 0,101(1100)_2=\frac{5*(2^4-1)+12}{2^3(2^4-1)+12}=\frac{29}{40};
  6. 0,c3(e)_{16}=\frac{195*15+14}{256-15}=\frac{2939}{3840}
Арифметические операции в системе счисления

Операции сложения, вычитания, умножения и деления в системе счисления с основанием p производятся аналогично тому, как они выполняются в десятичной системе счисления.

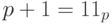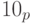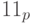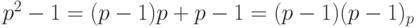Заметим, что p = 10_p, p + 1 = 11_p для любого основания p. Соответственно, предшествующим для числа 10_p является число p - 1, а следующим за ним - число 11_p. Для числа 100_p предшествующим является число p^2 - 1 = (p - 1)p + p - 1 = (p - 1)(p - 1)_p, а последующим - число 101_p.

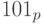Пример 13. Найдем сумму, разность, произведение и частное, а также результаты целочисленного деления для чисел 1120201_3 и 22_3 в троичной системе счисления:


Таким образом,

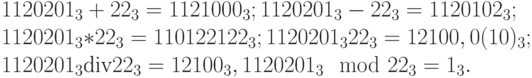
1120201_3 + 22_3 = 1121000_3; 1120201_3 - 22_3 = 1120102_3;\\ 1120201_3 * 22_3 = 110122122_3; 1120201_3 22_3 = 12100,0(10)_3;\\ 1120201_3 \text{div} 22_3 = 12100_3, 1120201_3 \mod 22_3 = 1_3.

Пример 14. Выполним операции сложения, вычитания, умножения и целочисленного деления в 16-ричной системе счисления для чисел c1e_{16} и b2_{16}:


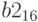  1. Найдем поразрядно сумму c1e + b2, начиная с младшего разряда. Имеем: e + 2 = 10, 1 + 1 + b = d. Поэтому c1e16 + b216 = cd016.
  2. Найдем разность c1e - b2. Имеем: e - 2 = c, 11 - b = 6, c - 1 = b. Следовательно, c1e16 - b216 = b6c16.
  3. Найдем произведение c1e * b2. Имеем: e * 2 = 1c, 1 * 2 + 1 = 3, с * 2 = 18. Поэтому c1e * 2 = 183c. Аналогично, e * b = 9a, 1 * b + 9 = 14, c * b + 1 = 85. Следовательно, c1e * b = 854a. Таким образом, c1e16 * b216 = 183c16 + 854a016 = 86cdc16.
  4. Разделим c1e на b2. Имеем: c1 = 1 * b2 + f, fe = 1 * b2 + 4c. Следовательно, c1e = 11 * b2 + 4c, так что c1e16 div b216 = 1116; c1e16 mod b216 = 4c16.

Замечание. Из утверждения 2 следует, что при s > 0

0,c_1\dotsc_k(c_{k+1}\dotsc_{k+s})_p=p^{-k}\left(c_1\dotsc_{kp}+\frac{c_{k+1}/dots_{k+sp}}{\frac{(p-1)\dots(p-1)}{s}p}\right)

Пример 15. Найдем представление числа 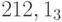212,1_3 в системе счисления с основанием 5.

Дальше >>
Лекция 1: 1234 || Лекция 2 >

Вопросы и ответы

вопросов: 0