Предобработка данных
Понижение размерности входов с помощью нейросетей
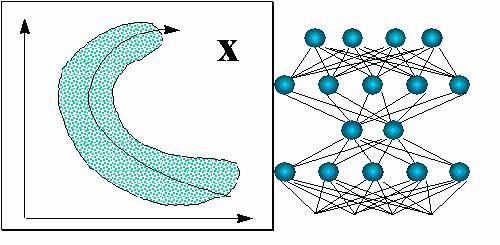
Для более глубокой предобработки входов можно использовать все богатство алгоритмов самообучающихся нейросетей, о которых шла речь ранее. В частности, для оптимального понижения размерности входов можно воспользоваться методом нелинейных главных компонент (см. рисунок 7.7).
Такие сети с узким горлом также можно использовать для восстановления пропущенных значений - с помощью итерационной процедуры, обобщающей линейный вариант метода главных компонент (см. рисунок 7.8).
Однако, такую глубокую "предобработку" уже можно считать самостоятельной нейросетевой задачей. И мы не будем дале углубляться в этот вопрос.
Квантование входов
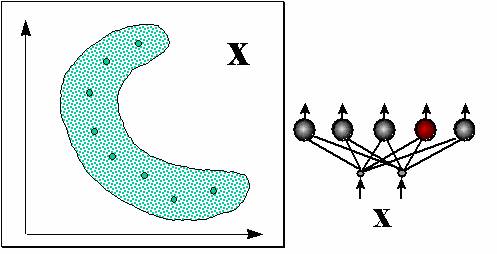
Более распространенный вид нейросетевой предобработки данных - квантование входов, использующее слой соревновательных нейронов (см. рисунок 7.9).
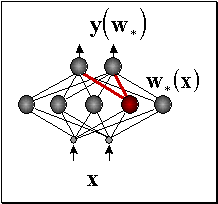
Нейрон-победитель является прототипом ближайших к нему входных векторов. Квантование входов обычно не сокращает, а наоборот, существенно увеличивает число входных переменных. Поэтому его используют в сочетании с простейшим линейным дискриминатором - однослойным персептороном. Получающаяся в итоге гибридная нейросеть, предложенная Нехт-Нильсеном в 1987 году, обучается послойно: сначала соревновательный слой кластеризует входы, затем выходным весам присваиваются значения выходной функции, соответствующие данному кластеру. Такие сети позволяют относительно быстро получать грубое - кусочно-постоянное - приближение аппроксимируемой функции (см. рисунок 7.10).
Особенно полезны кластеризующие сети для восстановления пропусков в массиве обучающих данных. Поскольку работа соревновательного
слоя основана на сравнении расстояний между данными и прототипами, осутствие у входного вектора 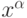 некоторых компонент не препятствует
нахождению прототипа-победителя: сравнение ведется по оставшимся компонентам
некоторых компонент не препятствует
нахождению прототипа-победителя: сравнение ведется по оставшимся компонентам 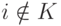 :
:

При этом все прототипы 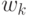 находятся в одинаковом положении.
Рисунок 7.11 иллюстрирует эту ситуацию.
находятся в одинаковом положении.
Рисунок 7.11 иллюстрирует эту ситуацию.

Рис. 7.11. Наличие пропущенных компонент не препятствует нахождению ближайшего прототипа по оставшимся компонентам входного вектора
Таким образом, слой квантующих входные данные нейронов нечувствителен к пропущенным компонентам, и может служить "защитным экраном" для минимизации последствий от наличия пропусков в обучающей базе данных.