Предобработка данных
Формирование оптимального пространства признаков
В типичной ситуации набор выходных, прогнозируемых, переменных фиксирован, и требуется подобрать наилучшую комбинацию ограниченного числа входных величин. Оценка значимости входов позволяет построить процедуру систематического предварительного подбора входных переменных - до этапа обучения нейросети. Для иллюстрации опишем две возможные стратегии автоматического формирования признакового пространства.
Последовательное добавление наиболее значимых входов
Один из наиболее очевидных способов формирования пространства признаков с учетом реальной значимости входов - постепенный подбор наиболее значимых входов в качестве очередных признаков. В качестве первого признака выбирается вход с наибольшей индивидуальной значимостью:
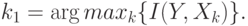
Вторым признаком становится вход, обеспечивающий наибольшую предсказуемость в паре с уже выбранным:
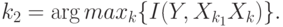
Такая процедура не гарантирует нахождения наилучшей комбинации входов, т.е. дает субоптимальный набор признаков, т.к. реально
рассматривается лишь очень малая доля от полного числа комбинаций входов, и значимость каждого нового признака зависит от сделанного
прежде выбора. Полный перебор, однако, практически неосуществим: выбор оптимальной комбинации входов при полном их числе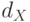 
требует перебора 
комбинаций.
Другим недостатком описанного выше подхода является необходимость подсчета кросс-энтропии в пространстве все более высокой
размерности по мере увеличения числа отобранных признаков. Ниже описана процедура, свободная от этого недостатка, основанная на
применении методики box-counting лишь в низкоразмерных пространствах (а именно - с размерностью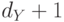 
).
Формирование признаков пространства методом ортогонализации
Следующая систематическая процедура способна итеративно выделять наиболее значимые признаки, являющиеся линейными комбинациями
входных переменных: 
(подмножество входов является частным случаем линейной комбинации, т.е. формально можно найти лучшее решение,
чем то, что доступно путем отбора наиболее значимых комбинаций входов).
Для определения значимости каждой входной компоненты будем использовать каждый раз индивидуальную значимость этого входа: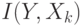 
.
Подсчитав индивидуальную значимость входов, находим направление в исходном входном пространстве, отвечающее наибольшей (нелинейной) чувствительности выходов к изменению входов. Это градиентное направление определит первый вектор весов, дающий первую компоненту пространства признаков:
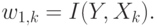
Следующую компоненту будем искать аналогично первой, но уже в пространстве перпендикулярном выбранному направлению, для чего спроектируем все входные вектора в это пространство:
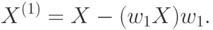
В этом пространстве можно опять подсчитать "градиент" предсказуемости, определив индивидуальную значимость
спроектированных входов, и так далее. На каждом следующем этапе подсчитывается индивидуальная значимость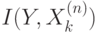 
для проекции входов 
,
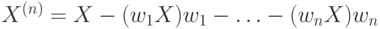что не требует повышения размерности box-counting анализа. Таким образом, описанная выше процедура позволяет формировать пространство
признаков произвольной размерности - без потери точности.
Заключение
Конечно, описанными выше методиками не исчерпывается все разнообразие подходов к ключевой для нейро-анализа проблеме формирования пространства признаков. Мы не упомянули, в частности, генетические алгоритмы, которые в совокупностью с методикой box-counting являются весьма перспективным инструментом. Ничего не было сказано также о методике разделения независимых компонент (blind signal separation), расширяющей анализ главных компонент. Необъятного не объять. Главное, чтобы за деталями не затерялся основополагающий принцип предобработки данных: снижение существующей избыточности всеми возможными способами. Это повышает информативность примеров и, тем самым, качество нейропредсказаний.