Обучение с учителем: Распознавание образов

Использование алгоритма back-propagation

При оценке значения алгоритма back-propagation важно различать нахождение градиента ошибки и его использование для обучения. Иногда под этим именем понимают именно конкретный тип итерационного обучения, предложенный в статье Румельхарта с соавторами. Этот простейший тип обучения (метод скорейшего спуска) обладает рядом недостатков. Существуют много гораздо более хороших алгоритмов обучения, использующих градиент ошибки более эффективно. Ниже мы перечислим некоторые из них, наиболее часто используемые на практике. Подчеркнем, однако, что все они так или иначе используют изложенный выше метод back-propagation для нахождения градиента ошибки.

Итак, простейший способ использования градиента при обучении - изменение весов пропорционально градиенту - т.н метод наискорейшего спуска:

Этот метод оказывается, однако, чрезвычайно неэффективен в случае, когда производные по различным весам сильно отличаются, т.е. рельеф функции ошибки напоминает не яму, а длинный овраг. (Это соответствует ситуации, когда активация некоторых из сигмоидных нейронов близка по модулю к 1 или, что то же самое - когда модуль некоторых весов много больше 1). В этом случае для плавного уменьшения ошибки необходимо выбирать очень маленький темп обучения, диктуемый максимальной производной (шириной оврага), тогда как расстояние до минимума по порядку величины определяется минимальной производной (длиной оврага). В итоге обучение становится неприемлемо медленным. Кроме того, на самом дне оврага неизбежно возникают осцилляции, и обучение теряет привлекательное свойство монотонности убывания ошибки.

Простейшим усовершенствованием метода скорейшего спуска является введение момента , когда влияние градиента на изменение весов накапливается со временем:

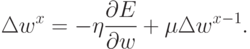
Качественно влияние момента на процесс обучения можно пояснить следующим образом. Допустим, что градиент меняется плавно, так что на протяжении некоторого времени его изменением можно пренебречь (мы находимся далеко от дна оврага). Тогда изменение весов можно записать в виде:

т.е. в этом случае эффективный темп обучения увеличивается, причем существенно, если момент . Напротив, вблизи дна оврага, когда направление градиента то и дело меняет знак из-за описанных выше осцилляций, эффективный темп обучения замедляется до значения близкого к :

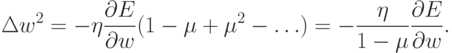
Дополнительное преимущество от введения момента - появляющаяся у алгоритма способность преодолевать мелкие локальные минимумы. Это свойство можно увидеть, записав разностное уравнение для обучения в виде дифференциального. Тогда обучение методом скорейшего спуска будет описываться уравненем движения тела в вязкой среде: . Введение момента соответствует появлению у такого гипотетического тела инерции, т.е. массы: . В итоге, "разогнавшись", тело может по инерции преодолевать небольшие локальные минимумы ошибки, застревая лишь в относительно глубоких, значимых минимумах.

Одним из недостатков описанного метода является введение еще одного глобального настроечного параметра. Мы же, наоборот, должны стремиться к отсутствию таких навязываемых алгоритму извне параметров. Идеальной является ситуация, когда все параметры обучения сами настраиваются в процессе обучения, извлекая информацию о характере рельефа функции ошибки из самого хода обучения. Примером весьма удачного алгоритма обучения является т.н. RPROP (от resilient - эластичный), в котором каждый вес имеет свой адаптивно настраиваемый темп обучения.

RPROP стремится избежать замедления темпа обучения на плоских "равнинах" ландшафта функции ошибки, характерного для схем, где изменения весов пропорциональны величине градиента. Вместо этого RPROP использует лишь знаки частных производных по каждому весу.

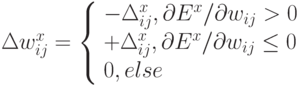
Величина шага обновления - своя для каждого веса и адаптируется в процессе обучения:

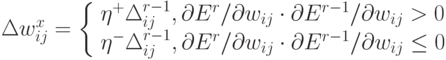
Если знак производной по данному весу изменил направление, значит предыдущее значение шага по данной координате было слишком велико, и алгоритм уменьшает его в

раз. В противном случае шаг увеличивается в раз для ускорения обучения вдали от минимума.

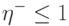
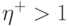
Мы не затронули здесь более изощренных методов обучения, таких как метод сопряженного градиента, а также методов второго порядка, которые используют не только информацию о градиенте функции ошибки, но и информацию о вторых производных. Их разбор вряд ли уместен при первом кратком знакомстве с основами нейрокомпьютинга.

Вычислительная сложность обучения

Ранее при обсуждении истории нейрокомпьютинга мы ссылались на относительную трудоемкость процесса обучения. Чтобы иметь хотя бы приблизительное представление о связанных с обучением вычислительных затратах, приведем качественную оценку вычислительной сложности алгоритмов обучения.

Пусть как всегда W - число синаптических весов сети (weights), а P - число обучающих примеров (patterns). Тогда для однократного вычисления градиента функции ошибки 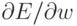требуется порядка PW операций. Допустим для простоты, что мы достаточно близки к искомому минимуму и можем вблизи этого минимума аппроксимировать функцию ошибки квадратичным выражением . Здесь 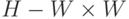- матрица вторых производных в точке минимума 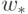. Оценив эту матрицу по локальной информации (для чего потребуется 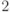операций метода back-propagation), можно попасть из любой точки в минимум за один шаг. На этой стратегии построены методы второго порядка (метод Ньютона). Альтернативная стратегия - найти требуемые параметров за шагов метода первого порядка, затратив на каждом шаге 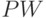операций. Именно такую скорость сходимости ( итераций) имеют лучшие алгоритмы первого порядка (например, метод сопряженного градиента). В обоих случаях оптимистическая оценка сложности обучения сети (т.к. она получена для простейшего из всех возможных - квадратичного - рельефа) составляет 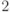операций.