Игра Эренфойхта и понижение мощности
Игра Эренфойхта
Вернемся от алгебры к логике и сформулируем общий критерий
элементарной эквивалентности двух интерпретаций некоторой
сигнатуры. Будем считать, что наша сигнатура содержит только
предикатные символы. (Это ограничение не очень существенно, так
как функцию 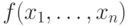 можно заменить предикатом
можно заменить предикатом 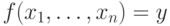 , имеющим на один аргумент больше.) Кроме
того, будем считать, что сигнатура конечна (в некоторый момент
наших рассуждений это будет существенно).
, имеющим на один аргумент больше.) Кроме
того, будем считать, что сигнатура конечна (в некоторый момент
наших рассуждений это будет существенно).
Критерий будет сформулирован в терминах некоторой игры, называемой игрой Эренфойхта. В ней участвуют два игрока, называемые Новатором ( Н ) и Консерватором ( К ). Игра определяется выбранной парой интерпретаций; как мы докажем, интерпретации элементарно эквивалентны тогда и только тогда, когда К имеет выигрышную стратегию в этой игре.
В начале игры Новатор объявляет натуральное число  . Далее они
ходят по очереди, начиная с Н ; каждый из игроков делает
. Далее они
ходят по очереди, начиная с Н ; каждый из игроков делает  ходов, после чего определяется победитель.
ходов, после чего определяется победитель.
На  -м ходу Н выбирает элемент в одной из интерпретаций (в
любой из двух, причем выбор может зависеть от номера хода) и
помечает его числом
-м ходу Н выбирает элемент в одной из интерпретаций (в
любой из двух, причем выбор может зависеть от номера хода) и
помечает его числом  . В ответ К выбирает некоторый элемент
из другой интерпретации и также помечает его числом
. В ответ К выбирает некоторый элемент
из другой интерпретации и также помечает его числом  . После
. После  ходов игра заканчивается. При этом в каждой интерпретации
ходов игра заканчивается. При этом в каждой интерпретации  элементов оказываются помеченными числами от
элементов оказываются помеченными числами от  до
до  (мы не учитываем, кто именно из игроков их пометил). Обозначим эти
элементы
(мы не учитываем, кто именно из игроков их пометил). Обозначим эти
элементы 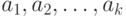 (для первой интерпретации;
элемент
(для первой интерпретации;
элемент  имеет пометку
имеет пометку  ) и
) и 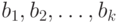 (для второй). Элементы
(для второй). Элементы  и
и 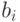 (с одним и тем
же
(с одним и тем
же  ) будем называть соответствующими друг другу. Посмотрим, найдется
ли предикат сигнатуры, который различает помеченные элементы
первой и второй интерпретации (то есть истинен на некотором
наборе помеченных элементов в одной интерпретации, но ложен на
соответствующих элементах другой). Если такой предикат найдется,
то выигрывает Новатор, в противном случае — Консерватор.
) будем называть соответствующими друг другу. Посмотрим, найдется
ли предикат сигнатуры, который различает помеченные элементы
первой и второй интерпретации (то есть истинен на некотором
наборе помеченных элементов в одной интерпретации, но ложен на
соответствующих элементах другой). Если такой предикат найдется,
то выигрывает Новатор, в противном случае — Консерватор.
Прежде чем доказывать, что эта игра дает критерий элементарной эквивалентности, рассмотрим несколько простых примеров.
- Среди элементов
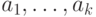 и
и 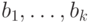 могут быть
одинаковые. Если в нашей сигнатуре есть предикат равенства и в
обеих интерпретациях он интерпретируется как совпадение
элементов, то Консерватор обязан повторять ходы, если их
повторил Новатор (скажем, если
могут быть
одинаковые. Если в нашей сигнатуре есть предикат равенства и в
обеих интерпретациях он интерпретируется как совпадение
элементов, то Консерватор обязан повторять ходы, если их
повторил Новатор (скажем, если  , а
, а 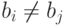 , то Новатор выигрывает, поскольку предикат равенства истинен в одной
интерпретации, но ложен на соответствующих элементах другой).
, то Новатор выигрывает, поскольку предикат равенства истинен в одной
интерпретации, но ложен на соответствующих элементах другой). - Если интерпретации изоморфны, то у Консерватора есть очевидный способ выиграть: изоморфизм заранее группирует все элементы в пары соответствующих. (Это согласуется с тем, что изоморфные интерпретации элементарно эквивалентны.)
-
Рассмотрим сигнатуру упорядоченных множеств (предикаты
 и
и  ) и ее естественные интерпретации в
) и ее естественные интерпретации в 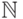 и
и  . Они не являются элементарно эквивалентными, поскольку среди натуральных
чисел есть наименьшее, а среди целых — нет. Покажем, что в игре
Эренфойхта для данных интерпретаций выигрывает Новатор.
. Они не являются элементарно эквивалентными, поскольку среди натуральных
чисел есть наименьшее, а среди целых — нет. Покажем, что в игре
Эренфойхта для данных интерпретаций выигрывает Новатор.Н объявляет, что игра будет проведена в два хода и на первом ходу помечает число
 из интерпретации
из интерпретации 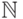 . В ответ К вынужден пометить некоторое число
. В ответ К вынужден пометить некоторое число  из
из  . На втором ходу Н помечает в
. На втором ходу Н помечает в  некоторое число, меньшее
некоторое число, меньшее  (например,
(например, 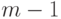 ). Теперь К проигрывает при любом ответном ходе,
поскольку пометить число, меньшее нуля, он не может.
). Теперь К проигрывает при любом ответном ходе,
поскольку пометить число, меньшее нуля, он не может. -
Для той же сигнатуры рассмотрим интерпретации в
 и
и  . Эти интерпретации не элементарно эквивалентны, поскольку порядок
на рациональных числах плотен, а на целых — нет. Покажем, что в
игре Эренфойхта снова выигрывает Новатор.
. Эти интерпретации не элементарно эквивалентны, поскольку порядок
на рациональных числах плотен, а на целых — нет. Покажем, что в
игре Эренфойхта снова выигрывает Новатор.Игра будет проходить в три хода. На первых двух ходах Н помечает числа
 и
и  из
из 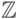 . К
должен пометить некоторые элементы
. К
должен пометить некоторые элементы 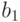 и
и 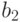 из
из  .
При этом должно быть
.
При этом должно быть 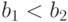 (иначе Н заведомо выиграет). Тогда на третьем ходу Н
помечает любое рациональное число, лежащее строго между
(иначе Н заведомо выиграет). Тогда на третьем ходу Н
помечает любое рациональное число, лежащее строго между 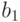 и
и 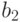 . Так как между
. Так как между  и
и  нет
натуральных чисел, К не может соблюсти требования игры и проигрывает при любом ходе.
нет
натуральных чисел, К не может соблюсти требования игры и проигрывает при любом ходе. -
Рассмотрим теперь упорядоченные множества
 и
и  . Как мы видели, они элементарно эквивалентны, и потому должна существовать
выигрышная стратегия для Консерватора. Как же он должен играть?
Кажется разумным поддерживать одинаковые расстояния между
соответствующими элементами в
. Как мы видели, они элементарно эквивалентны, и потому должна существовать
выигрышная стратегия для Консерватора. Как же он должен играть?
Кажется разумным поддерживать одинаковые расстояния между
соответствующими элементами в  и
и  .
Проблема в том, что в
.
Проблема в том, что в  некоторые
расстояния бесконечны (между элементами разных слагаемых). Что же делать Консерватору, если
Новатор пометил два таких элемента?
некоторые
расстояния бесконечны (между элементами разных слагаемых). Что же делать Консерватору, если
Новатор пометил два таких элемента?К счастью для К, он знает заранее, сколько ходов осталось до конца игры. Ясно, что если игра скоро кончится, то Н не удастся отличить бесконечное расстояние от достаточно большого. Более точно, если до конца игры остается
 ходов, то К может
считать все расстояния, большие или равные
ходов, то К может
считать все расстояния, большие или равные 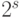 , бесконечно
большими. В конце (при
, бесконечно
большими. В конце (при 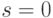 ) это означает, что все ненулевые
расстояния отождествляются (что правильно, так как в конце важен
лишь порядок). Таким образом, К стремится поддерживать такой
"инвариант" (как сказали бы программисты): соответствующие
элементы в
) это означает, что все ненулевые
расстояния отождествляются (что правильно, так как в конце важен
лишь порядок). Таким образом, К стремится поддерживать такой
"инвариант" (как сказали бы программисты): соответствующие
элементы в  и в
и в  идут в одном и том же порядке, и
расстояния между соответствующими парами соседей одинаковы (при
этом все бесконечно большие расстояния считаются одинаковыми).
Ясно, что такая стратегия гарантирует ему выигрыш; надо лишь
проверить, что поддержать инвариант можно.
идут в одном и том же порядке, и
расстояния между соответствующими парами соседей одинаковы (при
этом все бесконечно большие расстояния считаются одинаковыми).
Ясно, что такая стратегия гарантирует ему выигрыш; надо лишь
проверить, что поддержать инвариант можно.При очередном ходе Н возможны несколько случаев. Н мог разбить "конечный" (меньший
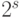 , где
, где  — число
оставшихся ходов) промежуток на две части. В этом случае
соответствующий промежуток в другом множестве также
"конечен" и имеет ту же длину, так что К должен лишь выбрать
элемент на том же расстоянии от концов. Пусть Н разбил
"бесконечный" (длины
— число
оставшихся ходов) промежуток на две части. В этом случае
соответствующий промежуток в другом множестве также
"конечен" и имеет ту же длину, так что К должен лишь выбрать
элемент на том же расстоянии от концов. Пусть Н разбил
"бесконечный" (длины 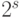 или больше) промежуток на две
части. Тогда хотя бы одна из частей будет иметь длину
или больше) промежуток на две
части. Тогда хотя бы одна из частей будет иметь длину 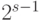 или больше, то есть на следующем шаге будет считаться
"бесконечной". Если обе части "бесконечны" (с точки
зрения следующего шага), то К должен разбить
"бесконечный" (длины
или больше, то есть на следующем шаге будет считаться
"бесконечной". Если обе части "бесконечны" (с точки
зрения следующего шага), то К должен разбить
"бесконечный" (длины 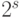 или более) промежуток другого
множества на две "бесконечные" (длины
или более) промежуток другого
множества на две "бесконечные" (длины 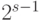 или более)
части; это, очевидно, возможно. Если одна часть "
бесконечна", а другая "конечна", то надо отложить то же
"конечное" расстояние в другом множестве. Наконец, обе
части не могут быть "конечными" (если каждая меньше
или более)
части; это, очевидно, возможно. Если одна часть "
бесконечна", а другая "конечна", то надо отложить то же
"конечное" расстояние в другом множестве. Наконец, обе
части не могут быть "конечными" (если каждая меньше 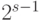 , то в сумме будет меньше
, то в сумме будет меньше 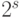 ).
).Наконец, новый элемент мог быть больше (или меньше) всех уже отмеченных элементов интерпретации; в этом случае К должен отметить элемент другой интерпретации, находящийся на том же расстоянии от наибольшего (наименьшего) отмеченного элемента (или на "бесконечном" расстоянии, если такова была ситуация с выбранным Н элементом).
