|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Организационно-экономическая система управления материальными запасами промышленных корпоративных систем
4.1. Базовые модели управления запасами
Управление запасами (материальнотехническое снабжение) - неотъемлемая часть работы фирм и организаций. Речь идет о запасах сырья, топлива, материалов, инструментов, комплектующих изделий, полуфабрикатов, готовой продукции на промышленном (или сельскохозяйственном) предприятии, о запасах товаров на оптовых базах, складах магазинов, на рабочих местах продавцов, наконец, у потребителей. Запасы постоянно расходуются и пополняются по тем или иным правилам, принятым на предприятии. Оптимизация этих правил, т. е. оптимальное управление запасами, дает большой экономический эффект.
Математическая теория управления запасами - крупная область экономико-математических исследований, получившая свое развитие начиная с пятидесятых годов ХХ века. Предложенная еще в 1915 г. Ф. Харрисом классическая модель теории управления запасами, называемая также моделью Вильсона (поскольку получила известность после публикации работы Р.Г. Вильсона в 1934 г.) - один из наиболее простых и наглядных примеров применения математического аппарата для принятия решений в экономической области. Формула оптимального размера заказа, полученная в модели Вильсона, широко применяется на различных этапах производства и распределения продукции. Она практически полезна для принятия решений при управлении запасами, в частности, приносит заметный экономический эффект [11]. Рассмотрим эту модель подробнее.
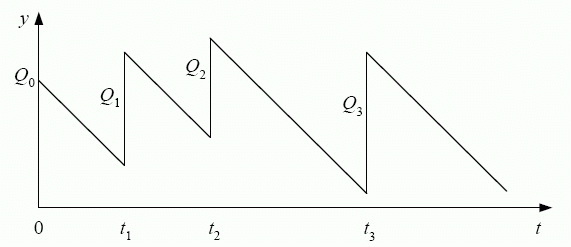
Классическая модель управления запасами.Пусть  - величина запаса некоторого товара на складе в момент времени
- величина запаса некоторого товара на складе в момент времени  ,
,  . Дефицит не допускается, т. е.
. Дефицит не допускается, т. е. 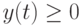 при всех
при всех  .
Товар пользуется равномерным спросом с интенсивностью
.
Товар пользуется равномерным спросом с интенсивностью  ,
т. е. за интервал времени
,
т. е. за интервал времени  со склада извлекается и поступает потребителям часть запаса величиной
со склада извлекается и поступает потребителям часть запаса величиной 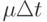 . В моменты времени
. В моменты времени 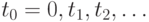 пополняется запас на складе - приходят поставки величиной
пополняется запас на складе - приходят поставки величиной 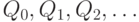 соответственно. Таким образом, изменение во времени величины запаса
соответственно. Таким образом, изменение во времени величины запаса 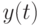 товара на складе изображается зубчатой ломаной линией (рис. 4.1), состоящей из наклонных и вертикальных звеньев, причем наклонные отрезки параллельны.
товара на складе изображается зубчатой ломаной линией (рис. 4.1), состоящей из наклонных и вертикальных звеньев, причем наклонные отрезки параллельны.
Таким образом, в момент 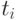 величина запаса на складе
величина запаса на складе 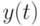 скачком увеличивается на
скачком увеличивается на 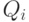 . Следовательно, функция
. Следовательно, функция 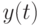 имеет разрывы в точках
имеет разрывы в точках 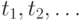 Для определенности будем считать, что эта функция непрерывна справа.
Для определенности будем считать, что эта функция непрерывна справа.
Пусть  - плата за хранение единицы товара в течение единицы времени. Поскольку можно считать, что величина запаса
- плата за хранение единицы товара в течение единицы времени. Поскольку можно считать, что величина запаса 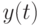 не меняется в течение интервала времени
не меняется в течение интервала времени 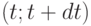 , где
, где 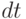 - дифференциал, т. е. бесконечно малая, то плата за хранение всего запаса в течение этого интервала времени равна
- дифференциал, т. е. бесконечно малая, то плата за хранение всего запаса в течение этого интервала времени равна 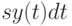 .
Следовательно, затраты за хранение в течение интервала времени
.
Следовательно, затраты за хранение в течение интервала времени  ,
где
,
где  - интервал планирования, пропорциональны (с коэффициентом пропорциональности
- интервал планирования, пропорциональны (с коэффициентом пропорциональности  ) площади под графиком уровня запаса на складе
) площади под графиком уровня запаса на складе 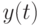 и равны
и равны
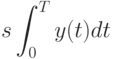
Пусть 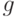 - плата за доставку одной партии товара. Примем для простоты, что она не зависит от размера поставки. Позже покажем, что если эта плата равна
- плата за доставку одной партии товара. Примем для простоты, что она не зависит от размера поставки. Позже покажем, что если эта плата равна 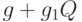 ,
где
,
где  - размер поставки, то оптимальный план поставки - тот же, что и при отсутствии линейного члена. Будет проанализирована и более сложная модель, в которой предусмотрена скидка с ростом поставки, приводящая к выражению
- размер поставки, то оптимальный план поставки - тот же, что и при отсутствии линейного члена. Будет проанализирована и более сложная модель, в которой предусмотрена скидка с ростом поставки, приводящая к выражению 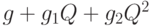 для платы за доставку одной партии товара размером
для платы за доставку одной партии товара размером  .
.
Пусть 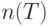 - количество поставок, пришедших в интервале
- количество поставок, пришедших в интервале  . При этом включаем поставку в момент
. При этом включаем поставку в момент  и не включаем поставку в момент
и не включаем поставку в момент 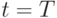 (если такая поставка происходит). Тогда суммарные издержки на доставку товара равны
(если такая поставка происходит). Тогда суммарные издержки на доставку товара равны 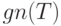 .
Следовательно, общие издержки (затраты, расходы) за время
.
Следовательно, общие издержки (затраты, расходы) за время 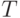 равны
равны
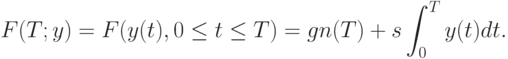
Запись 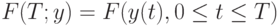 означает, что общие издержки зависят от значений функции
означает, что общие издержки зависят от значений функции 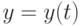 при всех
.
Символ
при всех
.
Символ  обозначает функцию как целое. То есть область определения
обозначает функцию как целое. То есть область определения 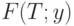 при фиксированном
при фиксированном  - не множество чисел, а множество функций.
- не множество чисел, а множество функций.
Общие издержки, очевидно, возрастают при росте горизонта планирования  .
Поэтому часто используют средние издержки, приходящиеся на единицу времени. Средние издержки за время
.
Поэтому часто используют средние издержки, приходящиеся на единицу времени. Средние издержки за время  равны
равны
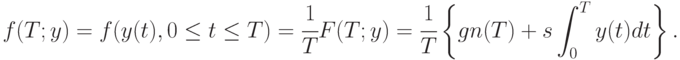
Поскольку товар отпускается со склада с постоянной интенсивностью (скоростью), дефицит не допускается, то доходы от работы склада пропорциональны горизонту планирования, средние доходы постоянны. Следовательно, максимизация прибыли эквивалентна минимизации издержек или средних издержек.
Если задать моменты прихода поставок и величины партий, то будет полностью определена функция  при всех
при всех 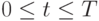 . Верно и обратное - фиксация функции
. Верно и обратное - фиксация функции  ,
, 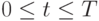 рассматриваемого вида (рис. 4.1) полностью определяет моменты прихода поставок и величины партий. И то, и другое будем называть планом поставок или планом работы системы управления запасами. Для ее оптимизации необходимо выбрать моменты времени
рассматриваемого вида (рис. 4.1) полностью определяет моменты прихода поставок и величины партий. И то, и другое будем называть планом поставок или планом работы системы управления запасами. Для ее оптимизации необходимо выбрать моменты времени 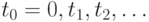 пополнения запаса на складе и размеры поставляемых партий товара
пополнения запаса на складе и размеры поставляемых партий товара 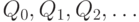 так, чтобы минимизировать средние издержки
так, чтобы минимизировать средние издержки 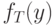 при фиксированном
при фиксированном  . Модель производственной ситуации (т. е. работы склада) описывается четырьмя параметрами -
. Модель производственной ситуации (т. е. работы склада) описывается четырьмя параметрами -  (интенсивность спроса),
(интенсивность спроса),  (стоимость хранения единицы продукции в течение единицы времени),
(стоимость хранения единицы продукции в течение единицы времени),  (стоимость доставки партии товара),
(стоимость доставки партии товара),  (горизонт планирования).
(горизонт планирования).
Решение задачи оптимизации.Поставленная задача оптимизации работы склада интересна тем, что неизвестно число 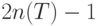 параметров, определяющих план поставок. Поэтому ее решение не может быть проведено с помощью стандартных методов теории оптимизации.
параметров, определяющих план поставок. Поэтому ее решение не может быть проведено с помощью стандартных методов теории оптимизации.
Решим эту задачу в три этапа. На первом установим, что оптимальный план следует искать среди тех планов, у которых все зубцы доходят до оси абсцисс, т. е. запас равен 0 в момент доставки очередной партии. Цель второго этапа - доказать, что все зубцы должны быть одной и той же высоты. Наконец, на третьем находим оптимальный размер поставки.
Оптимальный план.Найдем наилучший план поставок. План, для которого запас равен  (т. е.
(т. е. 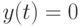 ) в моменты доставок очередных партий, назовем напряженным.
) в моменты доставок очередных партий, назовем напряженным.
Утверждение 1.Для любого плана поставок, не являющегося напряженным, можно указать напряженный план, для которого средние издержки меньше.
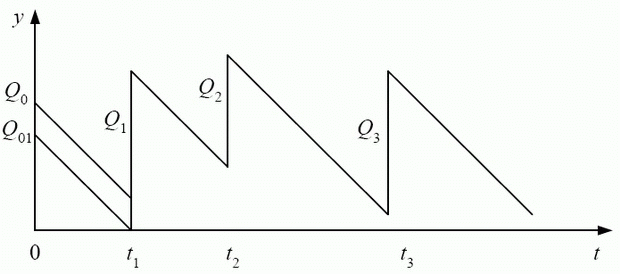
Покажем, как можно от произвольного плана перейти к напряженному плану, уменьшив при этом издержки. Пусть с течением времени при приближении к моменту 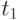 прихода поставки
прихода поставки 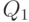 уровень запаса не стремится к 0, а лишь уменьшается до
уровень запаса не стремится к 0, а лишь уменьшается до  (где знак "минус" означает предел слева функции
(где знак "минус" означает предел слева функции 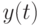 в точке
в точке 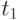 ). Тогда рассмотрим новый план поставок с теми же моментами поставок и их величинами, за исключением величин поставок в моменты
). Тогда рассмотрим новый план поставок с теми же моментами поставок и их величинами, за исключением величин поставок в моменты  и
и 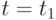 . А именно, заменим
. А именно, заменим  на
на 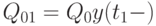 , а
, а 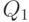 на
на  .
Тогда график уровня запаса на складе параллельно сдвинется вниз на интервале
.
Тогда график уровня запаса на складе параллельно сдвинется вниз на интервале  , достигнув
, достигнув  в
в 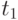 , и не изменится правее точки
, и не изменится правее точки 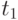 . Следовательно, издержки по доставке партий не изменятся, а издержки по хранению уменьшатся на величину, пропорциональную (с коэффициентом пропорциональности
. Следовательно, издержки по доставке партий не изменятся, а издержки по хранению уменьшатся на величину, пропорциональную (с коэффициентом пропорциональности  ) площади параллелограмма, образованного прежним и новым положениями графика уровня запаса на интервале
) площади параллелограмма, образованного прежним и новым положениями графика уровня запаса на интервале  (см. рис. 4.2).
(см. рис. 4.2).
В результате первого шага перехода получен план, в котором крайний слева зубец достигает оси абсцисс. Следующий шаг проводится аналогично, только момент времени  заменяется на
заменяется на 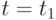 . Если есть такая возможность, второе наклонное звено графика уровня запаса на складе параллельно сдвигается вниз, достигая в крайней правой точке
. Если есть такая возможность, второе наклонное звено графика уровня запаса на складе параллельно сдвигается вниз, достигая в крайней правой точке 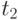 оси абсцисс.
оси абсцисс.
Аналогично поступаем со всеми остальными зубцами, двигаясь слева направо. В результате получаем напряженный план. На каждом шагу издержки по хранению либо сокращались, либо оставались прежними (если соответствующее звено графика не опускалось вниз). Следовательно, для полученного в результате описанного преобразования напряженного плана издержки по хранению меньше, чем для исходного плана, либо равны (если исходный план уже являлся напряженным).
Утверждение 1.Оптимальный план следует искать только среди напряженных планов, т. е. план, не являющийся напряженным, не может быть оптимальным.
Утверждение 2.Среди напряженных планов с фиксированным числом поставок минимальные издержки имеет тот, в котором все интервалы между поставками равны.
При фиксированном числе поставок затраты на доставку партий не меняются. Следовательно, достаточно минимизировать затраты на хранение.
Для напряженных планов размеры поставок однозначно определяются с помощью интервалов между поставками:

Действительно, очередная поставка величиной 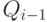 совпадает с размером запаса на складе в момент
совпадает с размером запаса на складе в момент 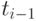 , расходуется с интенсивностью
, расходуется с интенсивностью  единиц товара в одну единицу времени и полностью исчерпывается к моменту
единиц товара в одну единицу времени и полностью исчерпывается к моменту 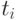 прихода следующей поставки.
прихода следующей поставки.
Для напряженного плана издержки по хранению равны
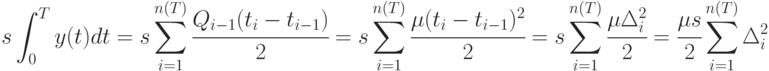
где 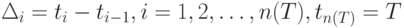 .
.
Ясно, что  - произвольные неотрицательные числа, в сумме составляющие
- произвольные неотрицательные числа, в сумме составляющие  . Следовательно, для минимизации издержек среди напряженных планов с фиксированным числом поставок достаточно решить задачу оптимизации
. Следовательно, для минимизации издержек среди напряженных планов с фиксированным числом поставок достаточно решить задачу оптимизации
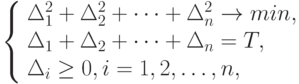
где 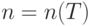 .
.
Полученная задача оптимизации формально никак не связана с логистикой, она чисто математическая. Для ее решения целесообразно ввести новые переменные 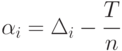 ,
,  .
.
Тогда
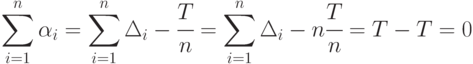
Поскольку 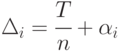 то
то  следовательно, с учетом предыдущего
следовательно, с учетом предыдущего
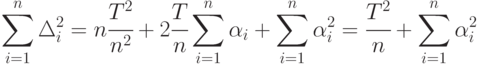
Сумма квадратов всегда неотрицательна. Она достигает минимума, равного 0, когда все переменные равны 0, т. е. при 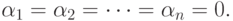 Тогда
Тогда

При этих значениях  выполнены все ограничения оптимизационной задачи. Итак, утверждение 2 доказано.
выполнены все ограничения оптимизационной задачи. Итак, утверждение 2 доказано.
Для плана с равными интервалами между поставками все партии товара имеют одинаковый объем. Для такого плана издержки по хранению равны
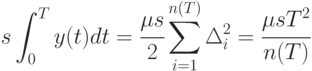 |
( T)}) |
Средние издержки (на единицу времени) таковы:
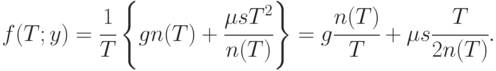 |
( T)}) |
Итак, минимизация средних издержек - это задача дискретной оптимизации. На третьем этапе построения оптимального плана необходимо найти натуральное число 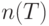 - самое выгодное число поставок.
- самое выгодное число поставок.
Поскольку к моменту  запас товара должен быть израсходован, то общий объем поставок за время
запас товара должен быть израсходован, то общий объем поставок за время  должен совпадать с общим объемом спроса, следовательно, равняться
должен совпадать с общим объемом спроса, следовательно, равняться 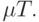 Справедливо балансовое соотношение (аналог закона Ломоносова-Лавуазье сохранения массы при химических реакциях):
Справедливо балансовое соотношение (аналог закона Ломоносова-Лавуазье сохранения массы при химических реакциях):
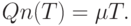
Из балансового соотношения следует, что
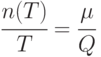
Средние издержки (на единицу времени) можно выразить как функцию размера партии
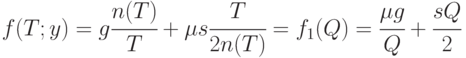 |
( 4.1) |
Задача состоит в минимизации  по
по 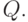 При этом возможная величина поставки принимает дискретные значения,
При этом возможная величина поставки принимает дискретные значения, 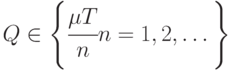 .
.
Изучим функцию 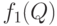 , определенную при
, определенную при  .
При приближении к 0 она ведет себя как гипербола, при росте аргумента - как линейная функция. Производная имеет вид
.
При приближении к 0 она ведет себя как гипербола, при росте аргумента - как линейная функция. Производная имеет вид
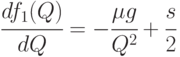
Производная монотонно возрастает, поэтому рассматриваемая функция имеет единственный минимум в точке, в которой производная равна 0, т. е. при
 |
( 4.2) |
Получена знаменитая "формула квадратного корня".
В литературе иногда без всяких комментариев рекомендуют использовать напряженный план, в котором размеры всех поставляемых партий равны 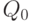 . К сожалению, получаемый таким путем план почти всегда не является оптимальным,т. е. популярная рекомендация неверна или не вполне корректна. Дело в том, что почти всегда
. К сожалению, получаемый таким путем план почти всегда не является оптимальным,т. е. популярная рекомендация неверна или не вполне корректна. Дело в том, что почти всегда
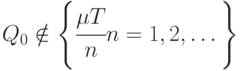
Всегда можно указать неотрицательное целое число  такое, что
такое, что
 |
( 4.3) |