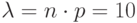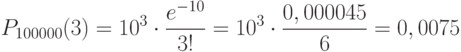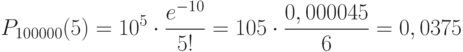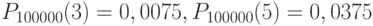Опубликован: 20.10.2016 | Доступ: платный | Студентов: 83 / 21 | Длительность: 07:27:00
Тема: Математика
Специальности: Математик, Преподаватель
Лекция 8:
Формула Пуассона
< Лекция 7 || Лекция 8 || Лекция 9 >
Ключевые слова: вероятность
Основные теоретические сведения
Если вероятность p наступления события A в каждом испытании постоянна и мала, а число независимых испытаний n достаточно велико, то вероятность наступления события A ровно m раз приближенно равна:
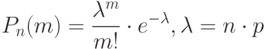 |
( 1.21) |
где m – число исходов, n – число независимых испытаний, p – вероятность.
Пример решения задачи
Задача: На предприятии изготовлено и отправлено заказчику 100000 бутылок пива. Вероятность того, что бутылка может оказаться битой, равна 0,0001. Найти вероятность того, что в отправленной партии будет ровно три и ровно пять битых бутылок.
< Лекция 7 || Лекция 8 || Лекция 9 >