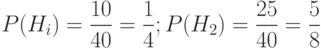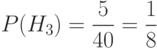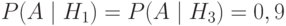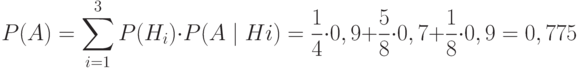Формула полной вероятности
Основные теоретические сведения
Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.
Вероятность события А, которое может наступить при условии появления одного из n несовместных событий (гипотез) 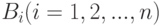 образующих полную группу, находят по формуле полной вероятности:
образующих полную группу, находят по формуле полной вероятности:
 |
( 1.17) |
где P(A) – вероятность события А;  – вероятность события
– вероятность события  ;
; 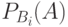 – условная вероятность события А, вычисленная при условии, что событие
– условная вероятность события А, вычисленная при условии, что событие  наступило;
наступило;  – сумма произведений вероятностей каждого из событий на соответствующую условную вероятность
– сумма произведений вероятностей каждого из событий на соответствующую условную вероятность
Сумма вероятностей гипотез 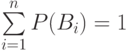
Пример решения задачи
Задача: Из 40 деталей 10 изготовлены в первом цехе, 25 - во втором, а остальные - в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех - с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?

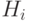 – выбранная деталь изготовлена в i цехе
– выбранная деталь изготовлена в i цехе