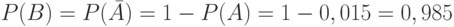Некоторые теоремы теории вероятностей

Основные теоретические сведения

Теорема 1. Вероятность суммы несовместных событий равна сумме вероятностей этих событий (ключевое слово "или"):

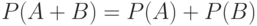( 1.9)

Теорема 2. Сумма вероятностей полной группы событий равна единице:

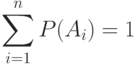( 1.10)

Теорема 3. Сумма вероятностей противоположных событий равна единице:

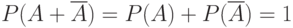( 1.11)

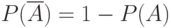( 1.12)

Теорема 4. Если событие А влечет за собой событие B, т.е. то

( 1.13)

Теорема 5. Вероятность суммы двух совместных событий вычисляется по формуле:

( 1.14)

Теорема 6. Вероятность совместного появления событий А и В равна произведению вероятности одного события на условную вероятность другого при условии, что первое событие произошло (ключевое слово "и"), и находится по формуле:

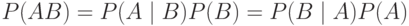( 1.15)

Теорема 7. Вероятность произведения независимых событий А и В равна произведению их вероятностей:

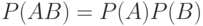( 1.16)

Пример решения задачи

Задача: Вероятность появления бракованной детали в партии равна 0,015. Найти вероятность того, что из этой партии будет изъята небракованная деталь.

Дано: P(A)=0,015	Решение: 1. А – деталь, изъятая из партии, бракованная В – из партии изъята небракованная деталь По теореме о вероятности противоположного события: Ответ: P(B)=0,985
P(B)=?