Опубликован: 20.10.2016 | Доступ: платный | Студентов: 83 / 21 | Длительность: 07:27:00
Тема: Математика
Специальности: Математик, Преподаватель
Лекция 2:
Треугольник Паскаля. Бином Ньютона
< Лекция 1 || Лекция 2 || Лекция 3 >
Основные теоретические сведения
Биноминальные коэффициенты очень красиво располагаются треугольником, в котором каждое число (кроме первого) является суммой двух предшествующих. Этот треугольник называется треугольник Паскаля.
| Показатель степени | Биноминальные коэффициенты | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 |  |
||||||||||
| 1 | 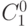 |
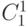 |
|||||||||
| 2 | 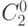 |
 |
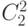 |
||||||||
| 3 | 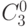 |
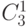 |
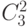 |
 |
|||||||
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ||
| n |  |
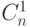 |
... | ... | ... | ... | ... | 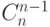 |
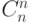 |
||
Эта таблица больше известна в виде значений:
| Показатель степени | Биноминальные коэффициенты | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | ||||||||||||
| 1 | 1 | 1 | |||||||||||
| 2 | 1 | 2 | 1 | ||||||||||
| 3 | |||||||||||||
| 1 | 3 | 3 | 1 | ||||||||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||||||
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | |
| n |  |
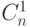 |
 |
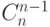 |
|||||||||
(n-я строка состоит из чисел 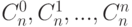 ).
).
Биномом Ньютона называют разложение вида:
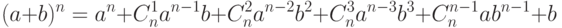 |
( 1.7) |
где 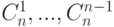 – биноминальные коэффициенты.
– биноминальные коэффициенты.
Пример решения задачи
Задача: Разложить по формуле бином 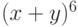 .
.
Решение: Используя треугольник Паскаля, находим биноминальные коэффициенты:
| Показатель степени | Биноминальные коэффициенты | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | ||||||||||||
| 1 | 1 | 1 | |||||||||||
| 2 | 1 | 2 | 1 | ||||||||||
| 3 | 1 | 3 | 3 | 1 | |||||||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||||||
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||
Используя полученные биноминальные коэффициенты, получаем разложение данного выражения:
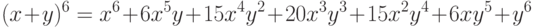
< Лекция 1 || Лекция 2 || Лекция 3 >
