НОУ ИНТУИТ | Теория экономических механизмов. Лекция 7: Двусторонняя торговля и теорема Вильямса

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 05.08.2011 | Доступ: платный | Студентов: 3 / 1 | Оценка: 4.50 / 3.50 | Длительность: 18:52:00

ISBN: 978-5-9963-0014-3

Темы: Математика, Экономика

Специальности: Математик, Экономист

|

Вам нравится? Нравится 44 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: В этой лекции мы рассмотрим результат, который является обобщением теоремы эквивалентности доходности (теоремы 4.1), — ее мы рассматривали, когда рассказывали об эффективных и оптимальных механизмах. Мы будем доказывать, что не существует механизмов, которые обладают определенным (достаточно сильным) набором свойств, в частности. что механизмы обычно не могут быть одновременно рациональными, эффективными и сбалансированными.

Введение

Основная идеология того, что будет происходить в этой лекции, такова. Мы хотим доказать, что не существует механизмов, которые решают такую-то задачу и обладают такими-то свойствами. Как это сделать? Чтобы доказать отсутствие таких механизмов, мы просто полностью классифицируем множество механизмов, обладаемых требуемыми свойствами. А затем покажем, что ни в каком из полученных случаев механизм нужную задачу не решает.

Один результат о классификации мы уже доказали, когда вели речь об аукционах; это была теорема об эквивалентности доходности. Она уже сама в чем-то является теоремой о классификации — утверждает, что правдивые механизмы почти полностью (с точностью до константы) классифицируются своими правилами распределения.

В частности, это значит, что эффективные правдивые механизмы вообще классифицированы уже очень хорошо, ведь правило распределения у них фиксировано. Это простое рассуждение — все, что нам потребуется для первого результата — теоремы Майерсона-Саттертуэйта о двусторонней торговле [59].

А затем мы рассмотрим значительно более общую формулировку, которая потребует более серьезных математических рассуждений. Это теорема Вильямса, которая классифицирует эффективные и правдивые механизмы в значительно большей общности, рассматривая правдивость interim с точки зрения математических ожиданий по распределениям типов других агентов [78]. Работу Вильямса можно рассматривать как обобщение и/или усиление достаточно большого числа результатов об эквивалентности, разработанных в теории экономических механизмов [37,38,42,49]. Применение теоремы Вильямса будет аналогичным теореме об эквивалентности доходности — мы установим, когда могут существовать одновременно рациональные, правдивые и эффективные механизмы. Но главное будет заключаться в том, что мы это докажем при весьма слабых предположениях.

Торговля между двумя участниками

Торговля между двумя участниками (bilateral trade) — это математическая модель очень простого экономического взаимодействия. Предположим, что друг с другом хотят провзаимодействовать два агента, один из которых хочет продать некую вещь, другой — ее же купить. Математически говоря, себестоимость вещи для продавца и ее ценность для покупателя представляют собой случайные величины. У продавца есть распределение его себестоимости ; в частности, $c\in[c_0,c_1]$ . У покупателя — свое распределение ценности ; в частности, $v\in[v_0,v_1]$ . Как водится в теории экономических механизмов, распределения случайных величин и всем известны, а конкретные стоимости, выпавшие в данном случае — нет. Наша задача — построить экономический механизм, который позволил бы продавцу и покупателю договориться друг с другом так, чтобы продажа совершалась тогда и только тогда, когда она выгодна обеим сторонам. При этом, конечно, и продавец, и покупатель могут пытаться лгать о своей себестоимости (ценности), если им это покажется выгодным.

Конечно, если 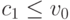$c_1 \le v_0$ , все в порядке, и тривиальный протокол "покупатель всегда платит цену 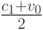$\frac{c_1+v_0}2$ , продавец всегда получает то же самое" решает проблему, ведь в этой ситуации 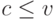$c\le v$ и продажа всегда выгодна и одной стороне и другой. Предположим, что конфликт может возникнуть, то есть v_0 < c_1 . Можно ли построить механизм так, чтобы торговля происходила тогда и только тогда, когда это выгодно обоим?

Формально говоря, механизм должен определить две вещи:

— сколько покупатель заплатит;
— сколько продавец получит.

Механизм эффективен, если объект продан тогда и только тогда, когда v>c .

Оказывается, что если мы не можем доплатить что-нибудь извне в эту экономическую систему, то ни один эффективный механизм не сможет обеспечить рациональность для агентов. Или ни один рациональный механизм не сможет обеспечить эффективность. Или ни один рациональный эффективный механизм не сможет обойтись без внешних денежных вливаний. В общем, это уж как посмотреть.

Теорема 7.1. (Майерсона-Саттертуэйта) В вышеописанной задаче не существует механизма, который бы был эффективен, правдив, рационален и у которого в то же время сходился бы бюджет.

Доказательство. Рассмотрим механизм VCG. Он работает в данном случае следующим образом:

Покупатель объявляет , продавец объявляет .
Если $v\le c$ , ничего не происходит.
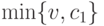Если , покупатель платит $\max\{c, v_0\}$ , а продавец получает $\min\{v,c_1\}$ .

Этот механизм, как и другие VCG-механизмы, обладает многими замечательными свойствами. Во-первых, он правдивый и эффективный, ведь объект продается тогда и только тогда, когда v>c . Во-вторых, он рационален:

у покупателя с ценностью 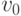ожидаемая прибыль равна , дальше — больше;
у продавца с ценностью 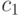ожидаемая прибыль равна , дальше — больше.

Но есть у него одна проблема — если v_0<c_1 , то, когда обмен вообще есть,

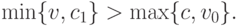
$\min\{v,c_1\}>\max\{c,v_0\}.$

То есть продавец в нетривиальной ситуации всегда получает строго больше, чем платит покупатель. Значит, VCG в этой ситуации не может сбалансировать бюджет.

Но теорема об эквивалентности доходности (теорема 4.1) гласит, что любой другой хороший механизм должен на константу отличаться от VCG. А в VCG продавец с себестоимостью 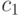c_1 не получает ровным счетом ничего. И это значит, что уменьшить доход продавца, сохранив рациональность, не получится. И покупатель с ценностью 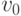v_0 тоже не извлекает никакой прибыли из этого механизма, а значит, увеличить платеж, сохранив рациональность, тоже не получится.

Итак, мы показали, что механизм VCG рационален, но у него не сходится баланс. А любой механизм, у которого сходится баланс, должен на константу отличаться от VCG, причем константа эта должна либо брать больше с покупателя, либо давать меньше продавцу. Но при любой из этих альтернатив теряется рациональность. Значит, для задачи двусторонней торговли не существует эффективных правдивых рациональных механизмов, у которых сходится бюджет.

Кстати говоря, в примере 5.4 мы рассматривали механизм AGV для этого примера и пришли к выводу, что он не будет рациональным; то есть механизм AGV теореме 7.1 тоже не противоречит.

Теорема Вильямса: дифференцируемый случай

В этом разделе мы докажем основной результат этой лекции — теорему Вильямса — не в полной общности, а в одном частном случае. Этот частный случай позволит использовать обычные производные вместо дифференциалов по направлениям, и поэтому изложение станет проще и яснее. Таким образом, мы сможем "на кошках" понять основную суть теоремы Вильямса, а затем уже доказать ее в полной общности.

Но сначала вспомним базовые определения и обозначения.

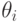Определение 7.1. Квазилинейная функция полезности агента с типом $\theta_i$ имеет вид

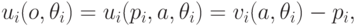
$u_i(o,\theta_i)=u_i(p_i,a,\theta_i)=v_i(a,\theta_i)-p_i,$

где исход 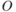определяет выбор 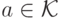$a\in\cal K$ из дискретного множества 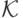$\cal K$ и выплату 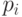p_i , производимую агентом.

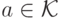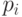Мы будем рассматривать исключительно агентов с квазилинейными преференциями (мы их уже упоминали в 2.5). У агента с квазилинейными преференциями есть функция оценки (valuation function) $v_i(a,\theta_i)$ , $a\in\cal K$ . Например, в аукционе, где продается одна вещь, ${\cal K}=\{0,1\}$ : агент либо получит эту вещь, либо не получит. Величина p_i в этом случае — выплата агента продавцу.

Теорема Вильямса — это усиленная версия принципа эквивалентности доходности; она классифицирует все "достаточно хорошие" механизмы и утверждает, что механизмы VCG покрывают все их множество. В этом параграфе мы установим основной результат для случая, когда типы агентов являются вещественными числами.

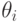Итак, предположим, что тип агента — это вещественное число, и он лежит в интервале $\theta_i\in[\underline{\theta}_i,\overline{\theta}_i]\subset\mathbb R$ . Обозначим через $\theta_i$ тип агента, а через 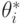$\theta^*_i$ — тип, который он сообщает механизму (к правдивости мы вернемся чуть позже).

Через 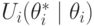$U_i(\theta^*_i\mid\theta_i)$ обозначим ожидаемую прибыль (utility) агента , которую можно по квазилинейности записать как

$U_i(\theta^*_i\mid\theta_i) = \mathbf E_{\mathbf\theta_{-i}}\left[\vphantom{1^2}u_i(p_i(\theta^*,\mathbf\theta_{-i}), a(\theta^*,\mathbf\theta_{-i}), \theta_i)\right] = \\ = \mathbf E_{\mathbf\theta_{-i}}\left[\vphantom{1^2}v_i(a(\theta^*,\mathbf\theta_{-i}),\theta_i)-p_i(\theta^*,\mathbf\theta_{-i})\right].$

Теперь понятно, что 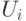U_i можно разложить на два слагаемых; обозначим их через 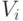V_i и P_i :

$V_i(\theta^*_i\mid\theta_i) &=& \mathbf E_{\mathbf\theta_{-i}}\left[v_i\left(\vphantom{1^2}a(\theta_i^*,\mathbf\theta_{-i}), \theta_i\right)\right],\\ P_i(\theta^*_i\mid\theta_i) &=& \mathbf E_{\mathbf\theta_{-i}}\left[\vphantom{1^2}p_i(\theta_i^*,\mathbf\theta_{-i})\right],\\ U_i(\theta^*_i\mid\theta_i) &=& V_i(\theta^*_i\mid\theta_i) - P_i(\theta^*_i\mid\theta_i).$

Теперь мы можем записать основные свойства механизмов в математических терминах. Правдивость механизма в наших обозначениях означает, что

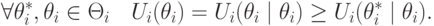
$\forall \theta_i^*,\theta_i\in\Theta_i\quad U_i(\theta_i) = U_i(\theta_i\mid\theta_i) \ge U_i(\theta^*_i\mid\theta_i).$

Рациональность означает, что ожидаемый доход агентов неотрицателен:

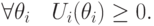
$\forall\theta_i\quad U_i(\theta_i)\ge 0.$

Баланс бюджета (ex ante!) означает, что ожидаемая сумма выплат неотрицательна:

$\mathbf E\left[\sum_{i=1}^Nv_i(a(\mathbf\theta),\theta_i)-U_i(\theta_i)\right] = \mathbf E\left[\sum_{i=1}^Np_i(\mathbf\theta)\right] \ge 0.$

Вспомним механизм VCG; это был эффективный механизм, выплаты в котором равнялись

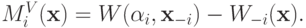
$M^V_i(\mathbf x) = W(\alpha_i,\mathbf x_{-i}) - W_{-i}(\mathbf x).$

Для того чтобы рассмотреть частный случай в этом параграфе, вспомним теорему об огибающей из математического анализа.

Теорема 7.2. (об огибающей) Рассмотрим задачу оптимизации

$M(a) = \max_x f(x,a).$

Если функция достаточно гладкая^{1Мы не будем здесь приводить точные условия, да и доказательство теоремы об огибающей, поскольку в следующем разделе все равно не будем ею пользоваться и докажем теорему в большей общности.}, то

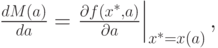
$\frac{dM(a)}{da}=\left.\frac{\partial f(x^*,a)}{\partial a}\right|_{x^*=x(a)},$

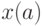где x(a) — точка, в которой достигается максимум.

Иначе говоря, достаточно продифференцировать по , по явному вхождению параметра, и вычислить в точке максимума.

Применим теперь теорему об огибающей к нашей ситуации:

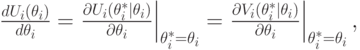
$\frac{dU_i(\theta_i)}{d\theta_i} = \left.\frac{\partial U_i(\theta^*_i\mid\theta_i)}{\partial \theta_i}\right|_{\theta_i^*=\theta_i} = \left.\frac{\partial V_i(\theta^*_i\mid\theta_i)}{\partial\theta_i}\right|_{\theta_i^*=\theta_i},$

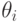потому что P_i от $\theta_i$ не зависит. Иначе говоря, получается, что

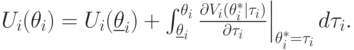
$U_i(\theta_i) = U_i(\underline{\theta}_i) + \int_{\underline\theta_i}^{\theta_i}\left.\frac{\partial V_i(\theta^*_i\mid\tau_i)}{\partial \tau_i}\right|_{\theta_i^*=\tau_i}d\tau_i.$

Это и дает нам результат об эквивалентности всех механизмов, потому что 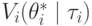$V_i(\theta^*_i\mid\tau_i)$ зависит только от правила 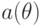$a(\mathbf\theta)$ и ценностей агентов 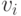v_i , но не от деталей реализации механизма.

Механизмы VCG, таким образом, покрывают все множество "хороших" механизмов. Это и есть теорема Вильямса.

Осталось понять, что такое "хороший" механизм. По идее, в теореме "хороший" должно означать "правдивый и эффективный". Мы прямо сейчас уже почти доказали эту теорему. Но, к сожалению, у нас тут появились еще какие-то ограничения на дифференцируемость функций 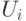U_i . Вообще говоря, нельзя применять теорему об огибающей к произвольным агентам. К сожалению, совсем произвольных агентов у нас все равно не получится, но получится существенно расширить область применимости теоремы. Поэтому в следующем разделе мы все докажем по-другому.

Важно также понимать, что ограничения на 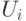U_i — это ограничения не на механизм, а на задачу, на допустимые множества агентов. Ослабляя эти ограничения, мы расширяем класс задач, к которым применима теорема о классификации. Но в любом случае теорема, которую мы докажем, классифицирует все правдивые эффективные механизмы; на механизм никаких дополнительных ограничений не накладывается.

Дальше >>

Авторизоваться

Теория экономических механизмов

Двусторонняя торговля и теорема Вильямса

Введение

Торговля между двумя участниками

Теорема Вильямса: дифференцируемый случай

Вопросы и ответы