Проективная размерность подпространств и проективная геометрия. Теорема о ранге матрицы
Проективная размерность подпространств и проективная геометрия PG(KV )
Если 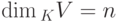 ,
, 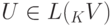 - линейное подпространство в K V, то определим проективную размерность
- линейное подпространство в K V, то определим проективную размерность
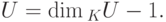
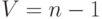 . Обозначая через G_i совокупность всех (i+1) -мерных линейных подпространств в K V, получаем (n-1) -мерную проективную геометрию PG(K V)={G0,G1,...,Gn-1},
где G0 - множество точек, G1 - множество прямых, G2 - плоскостей, Gi - множество i -мерных плоскостей, с отношением инцидентности
. Обозначая через G_i совокупность всех (i+1) -мерных линейных подпространств в K V, получаем (n-1) -мерную проективную геометрию PG(K V)={G0,G1,...,Gn-1},
где G0 - множество точек, G1 - множество прямых, G2 - плоскостей, Gi - множество i -мерных плоскостей, с отношением инцидентности  для
для  ,
,  , где
, где 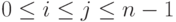 , означающим, что
, означающим, что 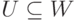 .
.Теорема о ранге матрицы
Пусть  - прямоугольная
- прямоугольная 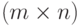 -матрица с элементами a_{ij} из поля K. Определитель
-матрица с элементами a_{ij} из поля K. Определитель 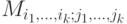 квадратной
квадратной  -матрицы, состоящей из элементов на пересечении k строк с номерами i1,...,ik и k столбцов с номерами j1,...,jk, называется минором k -го порядка матрицы A. Наивысший порядок ненулевого минора матрицы A обозначим через
-матрицы, состоящей из элементов на пересечении k строк с номерами i1,...,ik и k столбцов с номерами j1,...,jk, называется минором k -го порядка матрицы A. Наивысший порядок ненулевого минора матрицы A обозначим через  .
.
Теорема 9.16.1 (о ранге матрицы). Следующие четыре числовые характеристики матрицы  совпадают:
совпадают:
- r(A1,...,Am) (ранг системы строк, в Kn );
-
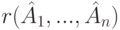 (ранг системы столбцов, в
(ранг системы столбцов, в  );
); - r(A) (наивысший порядок ненулевого минора);
- число ненулевых строк r в ступенчатом виде A матрицы A.
(Это совпадающее число называется рангом матрицы A } и будет обозначаться через r(A) ).
Доказательство разобьем на четыре леммы.
Лемма 9.16.2. Пусть матрица 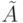 получена из матрицы A элементарным преобразованием строк (столбцов) 1-го или 2-го типа, тогда
получена из матрицы A элементарным преобразованием строк (столбцов) 1-го или 2-го типа, тогда  . Если A - ступенчатая форма, к которой приводится матрица A, то r(A)=r(A).
. Если A - ступенчатая форма, к которой приводится матрица A, то r(A)=r(A).
Доказательство проведем для преобразований строк (для столбцов все аналогично).
Случай 1. A'i=Ai+cAj,  ,
, 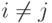 . Для k>r(A) рассмотрим минор
. Для k>r(A) рассмотрим минор 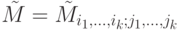 в
в  .
.
а) Если 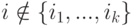 , то
, то  .
.
б) Если 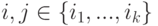 , то
, то  .
.
в) Если 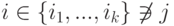 , то разложим определитель
, то разложим определитель 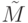 по i -й строке A'i=Ai+cAj в сумму двух определителей:
по i -й строке A'i=Ai+cAj в сумму двух определителей:  , так как
, так как  , поскольку
, поскольку 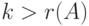 , определитель
, определитель  в качестве i -й строчки имеет часть строки Aj, но
в качестве i -й строчки имеет часть строки Aj, но 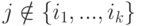 , и поэтому
, и поэтому  отличается от минора матрицы порядка k перестановкой двух строк, и поэтому
отличается от минора матрицы порядка k перестановкой двух строк, и поэтому  . Итак,
. Итак, 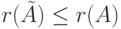 . Поскольку от A к
. Поскольку от A к 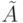 можно вернуться элементарным преобразованием строк, то
можно вернуться элементарным преобразованием строк, то 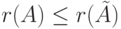 .
.
Случай 2.  разбирается аналогично (
разбирается аналогично (  ;
; 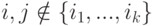 ;
; 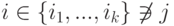 ).
).
Лемма 9.16.3 (о сохранении линейных соотношений между столбцами при элементарных преобразованиях строк). Пусть от матрицы A к матрице A' мы перешли элементарными преобразованиями строк, тогда столбцы матриц A и A' имеют одни и те же линейные соотношения, а именно, 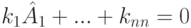 тогда и только тогда, когда
тогда и только тогда, когда 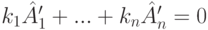 .
.
Доказательство. Ясно, что элементарные преобразования 1-го и 2-го типа для строк сохраняют линейное соотношение для столбцов и эти преобразования обратимы.
Следствие 9.16.4. Система столбцов 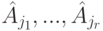 матрицы A линейно зависима (соответственно, линейно независима или является максимальной линейно независимой подсистемой в
матрицы A линейно зависима (соответственно, линейно независима или является максимальной линейно независимой подсистемой в 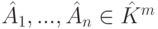 ) тогда и только тогда, когда соответствующая система столбцов (с теми же номерами)
) тогда и только тогда, когда соответствующая система столбцов (с теми же номерами) 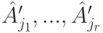 матрицы A' линейно зависима (соответственно линейно независима или является максимальной линейно независимой подсистемой в
матрицы A' линейно зависима (соответственно линейно независима или является максимальной линейно независимой подсистемой в 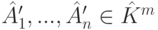 ).
).
Следствие 9.16.5. 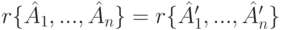 .
.
Лемма 9.16.6. Если A - ступенчатая матрица, то наивысший порядок ненулевого минора r(A) совпадает с числом r ненулевых строк.
- Минор r -го порядка на пересечении r ненулевых строк и столбцов, проходящих через уголки ступенек, является определителем треугольной матрицы с ненулевыми элементами на главной диагонали, и поэтому отличен от нуля.
- Все миноры, порядок которых больше r, нулевые, так как имеют нулевую строку.
Лемма 9.16.7. В ступенчатой матрице A ранг системы столбцов совпадает с числом r ненулевых строк (а именно, столбцы, проходящие через уголки ступенек, образуют максимальную линейно независимую подсистему столбцов).
- Указанные столбцы линейно независимы, так как проходят через
 -матрицу с ненулевым определителем.
-матрицу с ненулевым определителем. - Любой столбец ступенчатой матрицы является линейной комбинацией указанных.
Следствие 9.16.8 (алгоритм нахождения максимальной линейно независимой подсистемы в системе столбцов прямоугольной матрицы). От матрицы A перейдем к ступенчатой матрице A с помощью элементарных преобразований строк 1-го и 2-го типов, запомним номера столбцов j1,...,jr, проходящих через уголки ступенек в A, в матрице A возьмем столбцы с этими номерами 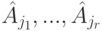 .
.
Пример 9.16.9.
Найти какую-либо максимальную линейно независимую подсистему строк в системе 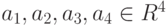 ,
,
Решение Записываем строки a1, a2, a3, a4 как столбцы и приводим полученную матрицу к главному ступенчатому виду с помощью элементарных преобразований строк:
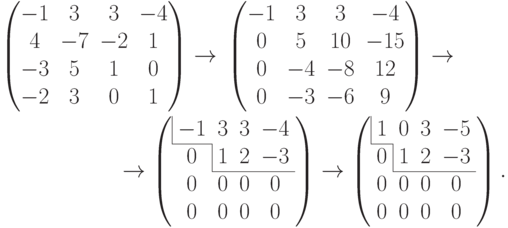
Записываем номера столбцов в ступенчатом виде, проходящие через уголки ступенек: 1, 2. Поэтому {a1,a2} - максимальная линейно независимая подсистема, a3=3a1+2a2, a4=-5a1-3a2 ; ранг системы строк a1, a2, a3, a4 равен 2.
Завершение доказательства теоремы о ранге:
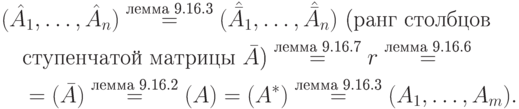
Теорема 9.16.10. Пусть  ,
,  . Тогда
. Тогда
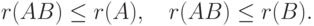
Доказательство. Пусть C=(cij)=AB. Тогда
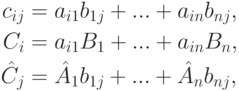
 и
и  .
.Следствие 9.16.11. При умножении на квадратную матрицу A с  ранг не меняется.
ранг не меняется.
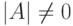
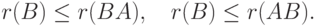
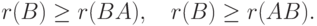
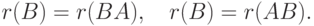
Задачи 9.16.12.
- В условиях теоремы:

- Если
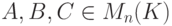 и ABC=0, то
и ABC=0, то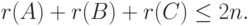
- Пусть
 ,
, 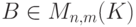 и m>n. Покажите, что
и m>n. Покажите, что 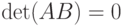 .
.Доказательство. Так как
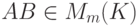 , то
, то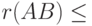
- Если
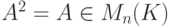 , то
, то
- Если
 и A2=A, AB=0=BA, то
и A2=A, AB=0=BA, то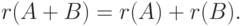
- Если
 , AB=BA,
, AB=BA,  и
и  , то
, то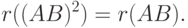
- Если
 ,
,  , то
, то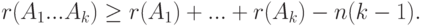
Теорема 9.16.13 (о факториальном ранге). Пусть 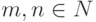 ,
,  . Ранг матрицы r(A) равен наименьшему числу k такому, что
. Ранг матрицы r(A) равен наименьшему числу k такому, что

Доказательство. Допустим, что 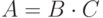 , где
, где 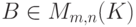 ,
, 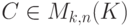 . Тогда система столбцов матрицы A линейно выражается через систему столбцов матрицы B (их k штук). Поэтому
. Тогда система столбцов матрицы A линейно выражается через систему столбцов матрицы B (их k штук). Поэтому 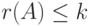 .
.
Пусть k=r(A). Выберем строки 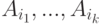 , образующие максимальную линейно независимую подсистему строк A1,...,Am матрицы A,
, образующие максимальную линейно независимую подсистему строк A1,...,Am матрицы A,
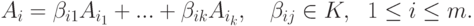
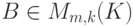 ,
, 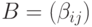 , и
, и 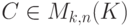 , для которой j -я строка
, для которой j -я строка 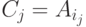 , j=1,...,k. Тогда
, j=1,...,k. Тогда 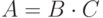 .
.Теорема 9.16.14 (теорема Кронекера—Капелли: критерий совместности и определенности системы линейных уравнений в терминах рангов матриц). Пусть  - система m линейных уравнений с n неизвестными,
- система m линейных уравнений с n неизвестными,  - матрица коэффициентов,
- матрица коэффициентов,
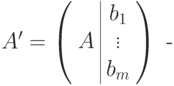
а) Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы коэффициентов A равен рангу расширенной матрицы 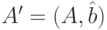 , r(A)=r(A').
, r(A)=r(A').
б) Система линейных уравнений определенная тогда и только тогда, когда r(A)=r(A')=n.
- Используя определение ранга матрицы с помощью столбцов, видим, что всегда
 .
. - Если (k1,...,kn) - решение, тот. е. столбцы матрицы A' линейно выражаются через столбцы матрицы A, следовательно,
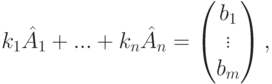
 , и поэтому r(A')=r(A).
, и поэтому r(A')=r(A). -
Пусть r(A')=r(A)=r. Тогда максимальная линейно независимая система столбцов матрицы A содержит r столбцов, и поэтому она является и максимальной линейно независимой системой столбцов матрицы A'. Таким образом, столбец
линейно выражается через эту систему столбцов матрицы A, а поэтому и через все столбцы матрицы A,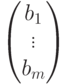 Итак, существует решение (k1,...,kn) системы линейных уравнений.
Итак, существует решение (k1,...,kn) системы линейных уравнений.
Второе доказательство. Элементарными преобразованиями приведем систему линейных уравнений к ступенчатому виду (ранги матриц не меняются при этом). Совпадение рангов означает отсутствие "экзотических" уравнений в ступенчатом виде, т. е. совместность системы линейных уравнений.
- Доказательство критерия определенности в терминах рангов). Если система определена, т. е. r(A)=r(A'), то она определена тогда и только тогда, когда в ступенчатом виде нет свободных неизвестных, т. е. r(A)=r(A')=n.

