Линейные преобразования линейных пространств столбцов
Линейные преобразования линейных пространств столбцов, задаваемые (прямоугольной) матрицей
Рассмотрим линейные пространства столбцов над полем K (например, над полем R действительных чисел)
![\begin{align*} & U=\hat K^n =
\left\{\left.X=\begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix}\right|
x_i\in K\right\},\\[3mm] & V=\hat K^m =
\left\{\left.Y=\begin{pmatrix}y_1\\\vdots\\y_m\end{pmatrix}\right|
y_i\in K\right\}.
\end{align*}](/sites/default/files/tex_cache/874dc8eadc72ab329297b2ee3f5cead3.png)
Каждая 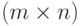 -матрица F=(fij),
-матрица F=(fij),  , задает отображение
, задает отображение 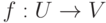 ,
,
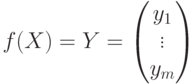

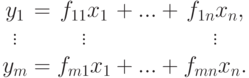

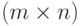 -матрицей F=(fij), обладает следующими свойствами:
-матрицей F=(fij), обладает следующими свойствами:-
f(X+X')=f(X)+f(X') для всех
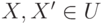 \textup;
\textup; -
f(cX)=cf(X) для всех
 ,
, 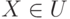 .
.
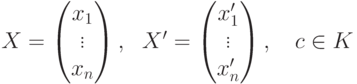
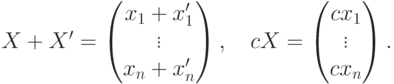
Замечание 7.0.7. Отображение 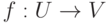 из одного линейного пространства U в другое линейное пространство V, удовлетворяющее свойствам
из одного линейного пространства U в другое линейное пространство V, удовлетворяющее свойствам
-
f(X+X')=f(X)+f(X') для всех
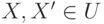 ,
, -
f(cX)=cf(X) для всех
 ,
, 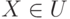 ,
,
называется линейным отображением (преобразованием). Тем самым мы показали, что отображение, задаваемое прямоугольной 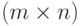 -матрицей F=(fij), определяет линейное преобразование соответствующих линейных пространств столбцов:
-матрицей F=(fij), определяет линейное преобразование соответствующих линейных пространств столбцов:
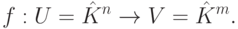
Пример 7.0.8. Если m=1, то имеем линейную функцию y=f1x1+...+fmxn
из 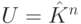 в
в  .
.
Пример 7.0.9. Поворот плоскости вокруг точки (0,0) на угол  является линейным отображением
является линейным отображением  , задаваемым матрицей поворота
, задаваемым матрицей поворота
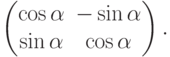
Теорема 7.0.10 (об однозначной определяемости матрицы, задающей линейное отображение столбцов). Пусть
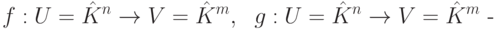
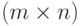 -матрицами F=(fij) и G=(gij) соответственно. Тогда f=g в том и только в том случае, когда F=G (т. е. fij=gij для всех i, j ).
-матрицами F=(fij) и G=(gij) соответственно. Тогда f=g в том и только в том случае, когда F=G (т. е. fij=gij для всех i, j ).- Если F=G, то ясно, что f=g.
- Пусть f=g. Рассмотримгде 1 стоит в j -й строке, а остальные элементы равны нулю. Тогда
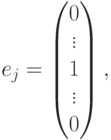 поэтому для любого i имеем fij=gij, т. е. F=(fij)=(gij)=G.
поэтому для любого i имеем fij=gij, т. е. F=(fij)=(gij)=G.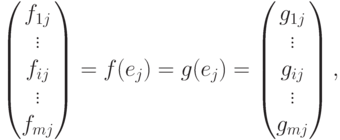
Теорема 7.0.11 (о задании любого линейного отображения линейных пространств столбцов матрицей). Пусть
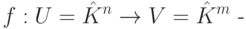
-
f(X+X')=f(X)+f(X') для всех
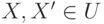 ,
, -
f(cX)=cf(X) для всех
 ,
, 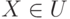 .
.
Тогда найдется (и единственная) 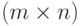 -матрица F=(fij) такая, что определяемое с ее помощью линейное отображение совпадает с линейным отображением f.
-матрица F=(fij) такая, что определяемое с ее помощью линейное отображение совпадает с линейным отображением f.

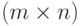 -матрицу F=(fij).
-матрицу F=(fij).Для любого

![\begin{mult}
\smash[b]{\begin{pmatrix}
y_1\\
\vdots\\
y_m
\end{pmatrix}} = f(X) =
x_1f(e_1)+...+x_nf(e_n)={}
\\
{}=
x_1
\begin{pmatrix}
f_{11}\\
\vdots\\
f_{m1}
\end{pmatrix} +... +
x_n
\begin{pmatrix}
f_{1n}\\
\vdots\\
f_{mn}
\end{pmatrix},
\end{mult}](/sites/default/files/tex_cache/0537a59f27f6476cdb1392fc9a60522a.png)
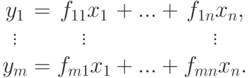
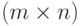 -матрицей F=(fij).
-матрицей F=(fij).
