НОУ ИНТУИТ | Введение в теорию вероятностей. Лекция 14: Характеристические функции

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Новосибирский Государственный Университет

Опубликован: 07.04.2008 | Доступ: платный | Студентов: 11 / 0 | Оценка: 4.56 / 4.32 | Длительность: 16:54:00

Тема: Математика

Специальности: Математик

Теги: алгебра, вычисления, графика, дискретное распределение, замечательный предел, коэффициент асимметрии, несовместное событие, полная группа, распределение бернулли, распределение коши, распределение пуассона, формула полной вероятности, функция Эйлера, цвета, элементы

|

Вам нравится? Нравится 73 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Определение характеристической функции и примеры вычисления. Свойства характеристических функций. Теорема непрерывности для характеристических функций. Доказательство центральной предельной теоремы и закона больших чисел в форме Хинчина

Определение и примеры

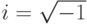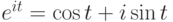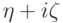В этой лекции $i=\sqrt{-1}$ - мнимая единица, - вещественная переменная, $e^{it}=\cos t+i\sin t$ - формула Эйлера, ${\mathsf E\,}(\eta + i\zeta)={\mathsf E\,}\eta + i\,{\mathsf E\,}\zeta$ - способ вычисления математического ожидания комплекснозначной случайной величины $\eta + i\zeta$ , если математические ожидания ее действительной ( $\eta$ ) и мнимой ( $\zeta$ ) частей существуют.

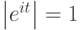Как всегда, модулем комплексного числа z=x+iy называется положительное число $|z|=\sqrt{x^2+y^2}$ , так что $\left|e^{it}\right|=1\vphantom{\int_{b_b}}$ .

Определение 47. Функция $\phi_\xi(t)={\mathsf E\,} e^{it\xi}$ вещественной переменной называется характеристической функцией случайной величины $\xi$ .

Пример 73. Пусть случайная величина $\xi$ имеет распределение Бернулли с параметром . Ее характеристическая функция равна

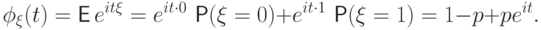
$\phi_\xi(t)={\mathsf E\,} e^{it\xi}=e^{it\cdot 0}\,\Prob(\xi=0)+ e^{it\cdot 1}\,\Prob(\xi=1)=1-p + pe^{it}.$

Пример 74. Пусть случайная величина $\xi$ имеет биномиальное распределение с параметрами и . Ее характеристическая функция равна

$\phi_\xi(t)&=&{\mathsf E\,} e^{it\xi}=\sum\limits_{k=0}^n e^{it\cdot k}\,\Prob(\xi=k) =\sum\limits_{k=0}^n e^{it\cdot k}\,C_n^k\,p^k\,{(1-p)}^{n-k}=\\ &=&\sum\limits_{k=0}^n C_n^k\,{\left(pe^{it}\right)}^k\,{(1-p)}^{n-k}= {\left(1-p + pe^{it}\right)}^n.$

Последнее равенство есть бином Ньютона.

Пример 75. Пусть случайная величина $\xi$ имеет распределение Пуассона с параметром $\lambda$ . Ее характеристическая функция равна

$\phi_\xi(t)&=&{\mathsf E\,} e^{it\xi}=\sum\limits_{k=0}^{\infty} e^{it\cdot k}\,\Prob(\xi=k)= \sum\limits_{k=0}^{\infty} e^{it\cdot k}\,\frac{\lambda^k}{k!}\,e^{-\lambda}=\\ &=&e^{-\lambda}\sum\limits_{k=0}^{\infty} \frac{{\left(\lambda \textstyle e^{it}\right)}^k}{k!}= e^{-\lambda}e^{\lambda \textstyle e^{it}}= \exp\{\lambda \left(e^{it}-1\right)\}.$

Пример 76. Пусть случайная величина $\xi$ имеет гамма-распределение с параметрами $\alpha$ и $\lambda$ . Ее характеристическая функция равна

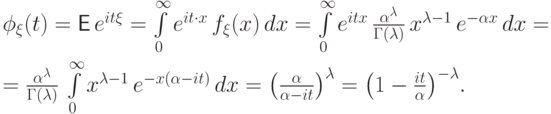
$\phi_\xi(t)&=&{\mathsf E\,} e^{it\xi}=\int\limits_{0}^{\infty} e^{it\cdot x}\,f_\xi(x)\,dx= \int\limits_{0}^{\infty} e^{itx}\,\frac{\alpha^\lambda}{\Gamma(\lambda)}\, x^{\lambda-1}\,e^{-\alpha x}\, dx= \\ &=&\frac{\alpha^\lambda}{\Gamma(\lambda)}\,\int\limits_{0}^{\infty} x^{\lambda-1}\, e^{-x(\alpha-it)}\, dx= {\left(\frac{\alpha}{\alpha-it}\right)}^{\lambda}= {\left(1-\frac{it}{\alpha}\right)}^{-\lambda}.$

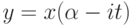Интеграл мы вычислили с помощью гамма-функции: замена $y=x(\alpha-it)$ дает

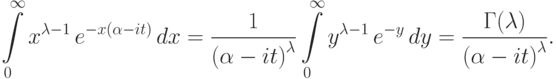
$\int\limits_{0}^{\infty} x^{\lambda-1}\, e^{-x(\alpha-it)}\, dx= \frac{1}{{(\alpha-it)}^\lambda}\int\limits_{0}^{\infty} {y}^{\lambda-1}\, e^{-y}\, dy= \frac{\Gamma(\lambda)}{{(\alpha-it)}^\lambda}.$

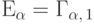В качестве следствия получим, что для случайной величины $\xi$ с показательным распределением ${\mathrm E}_\alpha=\Gamma_{\alpha,\,1}$ характеристическая функция равна $\phi_\xi(t)=\frac{\alpha}{\alpha-it}$ .

Пример 77. Пусть случайная величина $\xi$ имеет стандартное нормальное распределение. Ее характеристическая функция равна

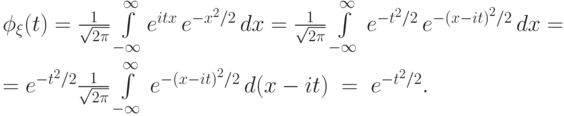
$\phi_\xi(t)&=& \frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^{\infty} e^{itx}\,e^{-x^2/2}\,dx =\frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^{\infty}\,e^{-t^2/2} \, e^{-{(x-it)}^2/2}\,dx= \\ &=& e^{-t^2/2} \frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^{\infty} \, e^{-{(x-it)}^2/2}\,d(x-it)\;=\; e^{-t^2/2}.$

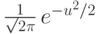При интегрировании мы выделили полный квадрат в показателе экспоненты и вспомнили, что интеграл по $\mathbb R$ от функции $\frac{1}{\smash{\sqrt{2\pi}}}\,e^{-u^2/2}$ равен единице.

Свойства характеристических функций

(Ф1). Характеристическая функция всегда существует:

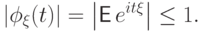
$|\phi_\xi(t)|=\bigl|{\mathsf E\,} e^{it\xi}\bigr|\le 1.$

Полезно вспомнить, что даже ${\mathsf E\,}\xi$ существует не всегда.

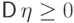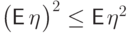Доказательство. Воспользуемся свойством ${\mathsf D\,}\eta\geq 0$ , равносильным неравенству $\bigl({\mathsf E\,}\eta\mspace{1mu}\bigr)^2\leq{\mathsf E\,}\mspace{-1mu}\eta^2$ :

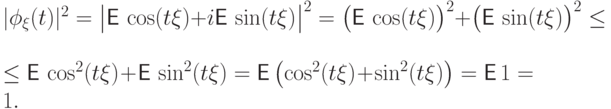
$|\phi_\xi(t)|^2&=& \bigl|{\mathsf E\,} \cos(t\xi)+ i{\mathsf E\,} \sin(t\xi)\bigr|^2= \bigl({\mathsf E\,} \cos(t\xi)\bigr)^2+\bigl({\mathsf E\,} \sin(t\xi)\bigr)^2 \le \\ &\le &{\mathsf E\,} \cos^2(t\xi)+{\mathsf E\,} \sin^2(t\xi) = {\mathsf E\,} \bigl(\cos^2(t\xi)+ \sin^2(t\xi)\bigr)={\mathsf E\,} 1=1.$

(Ф2). По характеристической функции однозначно восстанавливается распределение (функция распределения, плотность или таблица распределения). Другими словами, если две случайные величины имеют одинаковые характеристические функции, то и распределения этих величин совпадают.

Формулы, с помощью которых по характеристической функции восстанавливается распределение, в анализе называют формулами "обратного преобразования Фурье". Например, если модуль характеристической функции интегрируем на всей прямой, то у случайной величины есть плотность распределения и она находится по формуле

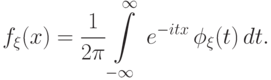
$f_\xi(x)=\frac{1}{2\pi}\int\limits_{-\infty}^{\infty}\,e^{-itx}\,\phi_\xi(t) \,dt.$

Ни одна из формул обратного преобразования Фурье нам не понадобится.

(Ф3). Характеристическая функция случайной величины 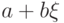$a+b\xi$ связана с характеристической функцией случайной величины $\xi$ равенством

$\phi_{a+b\xi}(t)={\mathsf E\,} e^{it(a+b\xi)}=e^{ita}{\mathsf E\,} e^{i(tb)\xi}=e^{ita}\,\phi_\xi(tb).$

Дальше >>

Авторизоваться

Введение в теорию вероятностей

Лекция 14: Характеристические функции

Определение и примеры

Свойства характеристических функций

Вопросы и ответы