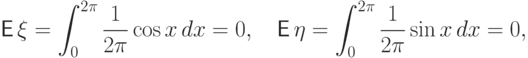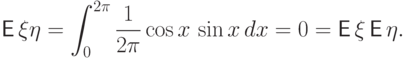Числовые характеристики распределений
Математическое ожидание случайной величины
Определение 35.
Математическим ожиданием  случайной величины
случайной величины  с дискретным распределением называется
число
с дискретным распределением называется
число
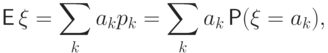
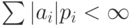 .
В противном случае говорят, что математическое
ожидание не существует.
.
В противном случае говорят, что математическое
ожидание не существует.Определение 36. Математическим ожиданием  случайной величины
случайной величины  с абсолютно непрерывным распределением с
плотностью
распределения
с абсолютно непрерывным распределением с
плотностью
распределения  называется число
называется число
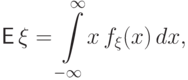
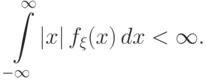
Математическое ожидание (иначе называемое средним значением или
первым моментом) имеет простой физический смысл: если на прямой
разместить единичную массу, поместив в точки  массу
массу  (для дискретного распределения) или "размазав" ее с плотностью
(для дискретного распределения) или "размазав" ее с плотностью  (для абсолютно непрерывного распределения),
то точка
(для абсолютно непрерывного распределения),
то точка  будет координатой центра тяжести
прямой.
будет координатой центра тяжести
прямой.
Пример 48.
Пусть случайная величина  равна числу очков, выпадающих при
одном
подбрасывании кубика. Тогда
равна числу очков, выпадающих при
одном
подбрасывании кубика. Тогда
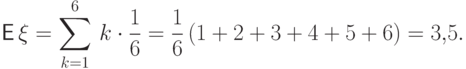
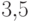 очка.
очка.Пример 49.
Пусть случайная величина  - координата точки, брошенной
наудачу
на отрезок
- координата точки, брошенной
наудачу
на отрезок ![[a,\,b]](/sites/default/files/tex_cache/d2524b9940ce1c636bfb26ae09a941d2.png) . Тогда
. Тогда
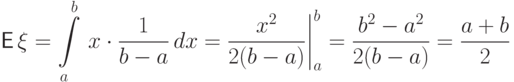
Свойства математического ожидания
Во всех свойствах предполагается, что рассматриваемые математические ожидания существуют.
(E1)
Для произвольной борелевской функции 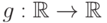
![{\mathsf E\,} g(\xi)=\begin{cases}
\displaystyle\sum\limits_k g(a_k)\Prob(\xi=a_k), &
\!\!\parbox[t]{8.5cm}{если распределение $\xi$ дискретно \\и ряд
абсолютно сходится;} \\[3.3mm]
\displaystyle\int\limits_{-\infty}^\infty g(x) f_\xi(x)\,dx, &
\!\!\parbox[t]{8.5cm}{если распределение $\xi$ абсолютно \\ непрерывно
и интеграл \\абсолютно сходится.}
\end{cases}](/sites/default/files/tex_cache/133bc61f82698fb3ac09cfadde0e214c.png)
Доказательство.
Мы докажем это свойство (как и почти все дальнейшие)
только для дискретного распределения.
Пусть 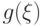 принимает значения
принимает значения 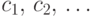 с
вероятностями
с
вероятностями
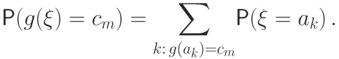
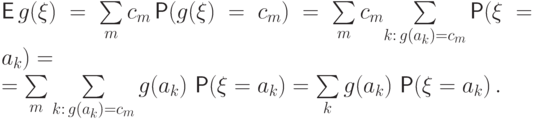
Следствие 10.
Математическое ожидание  существует тогда и только тогда,
когда
существует тогда и только тогда,
когда  .
.
Доказательство. Условием существование математического ожидания является
абсолютная сходимость ряда или интеграла
в определениях 35 и
36. Это в точности есть условие 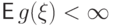 при
при  .
.
(E2) Математическое ожидание постоянной равно ей самой:  .
.
(E3) Постоянную можно вынести за знак математического ожидания:

Доказательство. Следует из свойства (E1) при 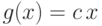 .
.
(E4) Математическое ожидание суммы любых случайных величин равно сумме их математических ожиданий, если только эти математические ожидания существуют:

Доказательство.
Пусть случайные величины  и
и  имеют дискретные
распределения со значениями
имеют дискретные
распределения со значениями  и
и  соответственно.
Для борелевской функции
соответственно.
Для борелевской функции  можно доказать
свойство, аналогичное
(E1).
Воспользуемся этим свойством для
можно доказать
свойство, аналогичное
(E1).
Воспользуемся этим свойством для  :
:
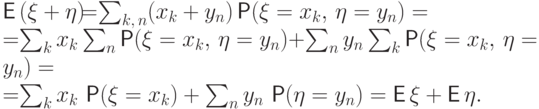
(E5)
Если 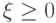 п.н., т.е. если
п.н., т.е. если  , то
, то  .
.
Замечание
Сокращение "п.н." читается как "почти наверное" и
означает "с вероятностью  ".
По определению, математическое ожидание - это числовая характеристика
распределения. Распределение
же не изменится от изменения случайной величины на множестве нулевой
вероятности.
Поэтому, например, даже если
".
По определению, математическое ожидание - это числовая характеристика
распределения. Распределение
же не изменится от изменения случайной величины на множестве нулевой
вероятности.
Поэтому, например, даже если 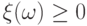 не при всех
не при всех 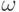 , а на множестве
единичной вероятности, математическое ожидание
, а на множестве
единичной вероятности, математическое ожидание  все равно
неотрицательно.
все равно
неотрицательно.
(E6)
Если 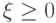 п.н. и при этом
п.н. и при этом  , то
, то  п.н.
п.н.
Доказательство.
Это свойство мы докажем, заранее предполагая, что  имеет
дискретное распределение
с неотрицательными значениями
имеет
дискретное распределение
с неотрицательными значениями  . Равенство
. Равенство 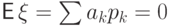 означает, что все слагаемые в этой сумме равны нулю, т.е. все вероятности
означает, что все слагаемые в этой сумме равны нулю, т.е. все вероятности 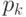 нулевые, кроме вероятности,
соответствующей значению
нулевые, кроме вероятности,
соответствующей значению 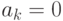 .
.
Из свойств (E5) и (E6) следуют полезные утверждения.
Следствие.
Если  п.н., то
п.н., то  .
.
Следствие.
Если 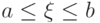 п.н., то
п.н., то 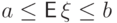 .
.
(E7)
Если  и
и 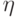 независимы и их математические
ожидания существуют, то
независимы и их математические
ожидания существуют, то 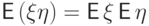 .
.
Доказательство. В дискретном случае
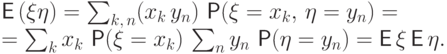
Замечание.
Обратное утверждение к свойству (E7)
неверно: из равенства 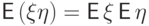 не следует независимость величин
не следует независимость величин  и
и 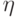 .
.
Пример 50.
Пусть  принимает значения
принимает значения  и
и  с вероятностями по
с вероятностями по 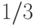 каждое,
и
каждое,
и  . Это зависимые случайные величины:
. Это зависимые случайные величины:
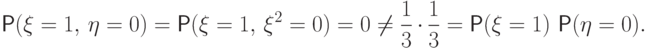
 и
и 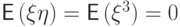 , поэтому
, поэтому 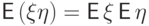 .
.Пример 51.
Пусть  , и пусть
, и пусть 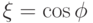 и
и  - заведомо зависимые случайные величины. Например:
- заведомо зависимые случайные величины. Например:
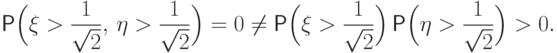
 ,
, 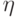 и
и 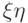 относительно нуля.
Действительно, по свойству
(E1) имеем
относительно нуля.
Действительно, по свойству
(E1) имеем