НОУ ИНТУИТ | Исследование операций и модели экономического поведения. Лекция 18: Выбор решений при неизвестных состояниях природы (игры с природой)

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Нижегородский государственный университет им. Н.И.Лобачевского

Опубликован: 26.04.2007 | Доступ: платный | Студентов: 42 / 6 | Оценка: 3.69 / 3.54 | Длительность: 14:45:00

ISBN: 978-5-9556-0072-7

Тема: Математика

Специальности: Математик

|

Вам нравится? Нравится 24 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Вероятностные модели выбора решений в условиях неопределенности. Прогнозирование и оценка состояний природы. Статистические игры. Принцип Байеса. Выбор простой гипотезы из конечного множества гипотез

Ключевые слова: работ, прибыль, функция, минимаксной стратегией, Исход, операции, состояния природы, класс, принятия решений, состояние природы, конфликт интересов, статистика, испытания, связь, вероятность, реакция, множества, априорное распределение, место, подмножество, объединение, априорный риск, апостериорный риск, усреднение полезностей, статистическая игра, смешанная стратегия, байесовская решающая функция, байесовский риск, простая гипотеза, статистическая гипотеза

Пример 4.1 (планирование посевов). Руководство сельскохозяйственного предприятия определяет вариант использования имеющихся посевных площадей (100 га), пригодных для выращивания двух типов зерновых культур. Урожайность этих культур и ожидаемые цены (за один центнер) при различных вариантах возможных погодных условий представлены в табл. 4.1.

Таблица 4.1.
Матрица H	Культуры:		Матрица С	Культуры:
Лето:	1	2	Лето:	1	2
Сухое	8	2	Сухое	5	8
Нормальное	8	6	Нормальное	5	6
Дождливое	4	10	Дождливое	6	4
Урожайность (ц/га)			Цены (тыс.руб./ц

Данные о затратах на проведение необходимых работ и о вероятной прибыли (также в зависимости от погодных условий предстоящего лета) содержатся в табл. 4.2. При этом прибыль a_ij, которая ожидается от продажи урожая культуры j, выращенной в погодных условиях i, определяется (в расчете на один гектар посевной площади) выражением

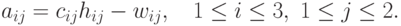
$a_{ij} = c_{ij} h_{ij} - w_{ij},\quad 1 \le i \le 3,\ 1 \le j \le 2.$

Таблица 4.2.
Матрица W	Культуры:		Матрица A	Культуры:
Лето:	1	2	Лето:	1	2
Сухое	6	8	Сухое	34	8
Нормальное	4	3	Нормальное	36	33
Дождливое	4	3	Дождливое	20	37
Затраты (тыс.руб./га)			Прибыль (тыс.руб./ц

Примем, что предприятие может одновременно засеять обе культуры, используя для первой из них часть площадей, задаваемую долей x 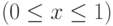$(0\le x \le 1)$ , а для второй - оставшуюся часть площадей, определяемую долей 1-x. Тогда ожидаемая прибыль от продажи урожая обеих культур (в расчете на один гектар используемой посевной площади) составит (как функция параметра x и погодных условий) величину

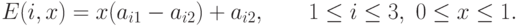
$E(i, x) = x(a_{i1} - a_{i2}) + a_{i2},\qquad 1 \le i \le 3,\ 0 \le x \le 1.$

При этом, в соответствии со значениями коэффициентов матрицы A из табл. 4.2,

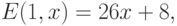( 17.1)

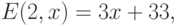( 17.2)

( 17.3)

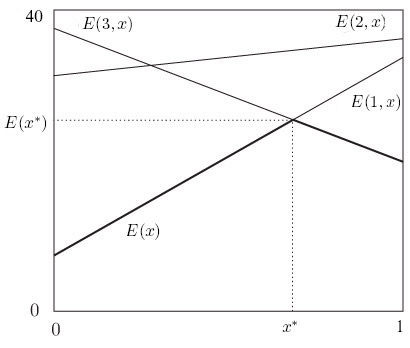
Зависимости (17.1)-(17.3) представлены на рис. 4.1.

Рис. 4.1.

Приняв некоторый план использования посевных площадей, определяемый параметром x, 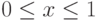$0\le x \le 1$ , предприятие гарантирует себе ожидаемую (удельную) прибыль

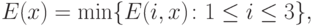$E(x) = \min\{E(i,x)\colon 1 \le i \le 3\},$

( 17.4)

которой соответствует (выделенная на рис. 4.1 толстыми линиями) нижняя огибающая семейства кривых (17.1)-(17.3). Согласно рисунку, стратегия x^*, максимизирующая удельную прибыль (17.4)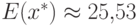, является решением уравнения E(1,x)=E(3,x). При этом x^*=29/43 и $E(x^\ast) \approx 25{,}53$ . Т.е. ожидаемая прибыль, соответствующая минимаксной стратегии x^*, составляет (для всей посевной площади) не менее 25,53 тыс. руб.

Напомним, что рассмотренный пример относится к задачам вида (1.17), в которых есть лишь одна сторона, являющаяся носителем интересов. Трудности выбора решений в таких задачах связаны с тем, что исход операции зависит от некоторых неконтролируемых параметров, значения которых влияют на исход операции, но не известны оперирующей стороне. Эти параметры (их роль в рассмотренном выше примере играли неизвестные погодные условия) обычно называют состояниями природы. В связи с этим, обсуждаемый класс задач принятия решений в условиях неопределенности определяют также как игры с природой. При этом следует иметь в виду, что в любой конкретной операции природа не является носителем чьих-либо интересов. Это обстоятельство открывает определенные возможности для прогнозирования неизвестных состояний природы (заметим, такие возможности обычно не могут быть использованы для прогнозирования действий сторон, имеющих свои интересы в операции).

Дальше >>

Авторизоваться

Исследование операций и модели экономического поведения

Лекция 18: Выбор решений при неизвестных состояниях природы (игры с природой)

Вопросы и ответы