|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Сделки без побочных платежей
Арбитражные схемы
Вернемся к рассмотрению операций, описываемых играми двух лиц с непостоянной суммой. При этом мы ограничимся классом конечных неантагонистических игр, нормальная форма которых характеризуется биматричным представлением.
Случай, когда участники такой игры действуют независимо1Такое поведение, называемое также некооперативным или бескоалиционным, может являться
следствием условий операции, например, следствием существования
антитрестовского законодательства и т.п., уже рассматривался во второй
лекции. В частности, было установлено, что единственное устойчивое решение  неантагонистической биматричной игры
(если оно достигается в смешанных
стратегиях) оказывается неэффективным в силу характера поведения игроков в
этом (единственном) устойчивом решении. Этот эффект "антагонизма
поведения без антагонизма интересов" подробно обсуждался
в
"Стратегическое равновесие в 2 x 2 играх"
.
неантагонистической биматричной игры
(если оно достигается в смешанных
стратегиях) оказывается неэффективным в силу характера поведения игроков в
этом (единственном) устойчивом решении. Этот эффект "антагонизма
поведения без антагонизма интересов" подробно обсуждался
в
"Стратегическое равновесие в 2 x 2 играх"
.
С другой стороны, в том же классе задач возможны ситуации существования нескольких устойчивых решений, часть из которых являются эффективными. При этом возникают проблемы выбора конкретного решения, связанные с тем, что ситуации равновесия, более выгодные для одной стороны, оказываются менее выгодными для другой. Если же стороны выберут действия, соответствующие разным состояниям равновесия, то результат такого несогласованного выбора может не обладать свойствами поведения в равновесии (см. обсуждение задачи строительства с долевым участием "Стратегическое равновесие в 2 x 2 играх" ).
Таким образом, в случае непротивоположных интересов сторон, достижение устойчивых и одновременно эффективных решений требует организации соответствующего взаимодействия участников операции. Практика выработала ряд механизмов такого кооперативного поведения, ядром которых является принятие сторонами некоторого соглашения о совместных действиях. Модели таких операций обычно называют кооперативными играми.
К числу ключевых вопросов организации кооперативного поведения, которое стимулируется стремлением к достижению ситуаций, оптимальных по Парето, относится обеспечение гарантий выполнения принятых соглашений всеми участвующими сторонами. Одним из путей создания таких гарантий является введение некоторого контролирующего органа, которому подчиняются все игроки. Типичным учреждением такого рода является арбитраж2 Арбитраж - способ разрешения споров (главным образом имущественного характера), при котором стороны обращаются к арбитрам (посредникам), избираемым самими сторонами или назначаемым по их соглашению либо в порядке, установленном законом. (или третейский суд). Модели кооперативного поведения, которые учитывают существование системы стабилизации соглашений, основанной на арбитраже, называются арбитражными схемами.
Юридические и технические аспекты организации арбитража выходят за рамки этой книги. Для наших целей существенно лишь то, что система арбитража обеспечивает устойчивость соглашений сторон. Поэтому в центре рассмотрения будет исследование характера сделок (договоров), совершаемых сторонами и подпадающих под юрисдикцию арбитража. Предлагаемые ниже модели не содержат описаний самого процесса переговоров сторон, могущего включать торг, блеф и другие психологические маневры. Цель проводимого моделирования заключается в предсказании той сделки, на которую согласятся стороны, руководствующиеся некоторыми достаточно естественными принципами. В связи с этим, арбитражные схемы называют также задачами о сделках.
Множество допустимых сделок
Примем, что стороны P1 и P2, интересы которых
описываются  матрицами A и B с коэффициентами aij
и bij,
матрицами A и B с коэффициентами aij
и bij,  ,
,  ,
могут вступать в кооперацию, допускающую совместный выбор стратегий.
,
могут вступать в кооперацию, допускающую совместный выбор стратегий.
Замечание 3.1 (о трансферабельности полезностей и побочных платежах ). Построение модели операции в нормальной форме, проведенное в первой лекции, включало описание интересов сторон с помощью вещественных функций, сопоставляющих исходам операции некоторые числовые значения, которые мы интерпретировали как полезность этих исходов (см. определение в "Математическая модель задачи выбора решений" ). Введение такого представления о полезности позволило охарактеризовать целенаправленное поведение участников операции как их стремление к максимизации соответствующих вещественных функций.
Далее, рассматривая антагонистические взаимодействия (см. замечание в "Математическая модель задачи выбора решений" ), мы приняли, что полезности исходов для одной стороны противоположны (по знаку) полезностям этих же исходов для другой стороны. Однако для задач с непротивоположными интересами вопрос о соотнесении полезностей сторон не рассматривался, поскольку их независимое поведение не требовало такого сопоставления. Допущение кооперации участников операции ставит новый вопрос о том, может ли одна сторона оплатить сотрудничество другой стороны, используя для этого часть своего выигрыша. Такая оплата (если она возможна) называется побочным платежом.
Сама возможность таких платежей предполагает, что выигрыш одной стороны представляет интерес для другой. Но так бывает не всегда. Например, вопросы престижа могут сделать выигрыш ценным для одной стороны, но практически ничего не стоящим для другой. Конкретная физическая форма выигрыша (например, здания, сооружения, транспортные системы, сельскохозяйственные угодья и т.п.) также может представлять интерес для одной стороны и не представлять такого интереса для другой стороны в силу различий характера их экономической деятельности.
Классический подход к решению этой проблемы обмена полезностями состоит во введении специального товара, полезность которого была бы линейна (т.е. полезность некоторого его количества прямо пропорциональна этому количеству) и который мог бы выступать как средство обмена (во многих ситуациях указанную функцию могут выполнять деньги). В этом случае побочные платежи могли бы выражаться в единицах такого товара.
Мы ограничимся случаем, когда функции выигрышей сторон можно интерпретировать как линейно трансферабельные полезности. При этом передача части полезности от одного игрока к другому не изменяет их общей (суммарной) полезности.
Заметим, что и при линейно трансферабельных полезностях побочные платежи могут оказаться нереализуемыми, как вследствие недробимости выигрышей, так и вследствие существующего правового регулирования отношений. Поэтому мы сначала рассмотрим кооперацию без побочных платежей, а затем исследуем взаимодействия с побочными платежами.
Для целей дальнейшего рассмотрения удобно представлять пару (aij,bij), соответствующую согласованному использованию сторонами P1 и P2 чистых стратегий i и j, как точку на плоскости. При этом условимся, что абсцисса (u) соответствует выигрышам (полезностям) стороны P1, а ордината (v) - выигрышам стороны P2. Множество всех таких точек, соответствующих конкретной задаче (т.е. конкретным матрицам A и B ), обозначим символом R:
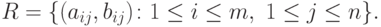 |
( 14.1) |
