Роевые и муравьиные алгоритмы
11.5. Основные модификации РА
В настоящее время РА применяется при решении многих проблем, включая стандартные задачи численной и комбинаторной оптимизации, обучение нейронных сетей и т.д. и показал неплохие результаты. Но в некоторых случаях изложенная базовая версия РА имеет тенденцию к преждевременной сходимости и не находит оптимальные решения. Поэтому разработан ряд модификаций РА, основные из которых включают введение веса инерции, ограничение и сужение диапазона скорости частиц, различные способы определения персональных и глобальных позиций и различные модели скорости, которые будут рассмотрены ниже. При этом важнейшим аспектом, который определяет эффективность и точность алгоритма оптимизации является соотношение (exploration-exploitation) исследование-локализация пространства поиска. Исследование (exploration) характеризует способность алгоритма исследовать различные области пространства поиска (расширять его) для того, чтобы локализовать хорошее решение. С другой стороны локализация (exploitation – разработка, эксплуатация) определяет способность алгоритма концентрировать поиск в перспективной области для того, чтобы улучшить решение. Хороший алгоритм оптимизации должен поддерживать баланс между этими двумя противоположными свойствами.
Ограничение скорости является одним из основных методов повышения эффективности РА, где свойства исследования-локализации пространства поиска определяются уравнением изменения скорости (11.2) (или 11.5), которое содержит три слагаемых, регулирующих величину и направление изменения скорости частицы. Уже в ранних работах было обнаружено, что часто скорость частиц резко увеличивается, особенно это характерно для частиц, далеких от лучших локальных и глобальных позиций. В результате частицы получают большие положительные приращения и покидают границы "зоны интереса" в пространстве поиска (частицы расходятся). Поэтому желательно ограничить изменение скоростей частиц в некотором диапазоне. Если скорость частицы превышает некоторый порог, то она искусственно устанавливается в некоторое максимально допустимое значение. Пусть  обозначает максимально допустимую скорость в
обозначает максимально допустимую скорость в  -й компоненте. Тогда скорость частицы регулируется (перед изменением позиции согласно уравнению (11.1)) следующим образом
-й компоненте. Тогда скорость частицы регулируется (перед изменением позиции согласно уравнению (11.1)) следующим образом
 |
( 11.11) |
где  вычисляется в соответствии с (11.2) (или (11.5)). При этом значение
вычисляется в соответствии с (11.2) (или (11.5)). При этом значение  имеет большое значение, поскольку оно определяет уровень разбиения пространства поиска путем ограничения увеличения скорости. Большое значение
имеет большое значение, поскольку оно определяет уровень разбиения пространства поиска путем ограничения увеличения скорости. Большое значение  способствует глобальному исследованию пространства поиска, в то время как малое – локализации хорошего решения. Кроме этого, малые значения увеличивают число итераций при поиске решения. Более того, при этом рой может попасть в ловушку локального экстремума. С другой стороны большие значения
способствует глобальному исследованию пространства поиска, в то время как малое – локализации хорошего решения. Кроме этого, малые значения увеличивают число итераций при поиске решения. Более того, при этом рой может попасть в ловушку локального экстремума. С другой стороны большие значения  увеличивают риск пропуска перспективной области. Частицы могут "перепрыгнуть" через хорошие решения и продолжать поиск в неперспективной области пространства поиска. Часто
увеличивают риск пропуска перспективной области. Частицы могут "перепрыгнуть" через хорошие решения и продолжать поиск в неперспективной области пространства поиска. Часто  полагают
полагают
 |
( 11.12) |
где  и
и  соответственно максимальное и минимальное значение
соответственно максимальное и минимальное значение  -ой компоненты, а
-ой компоненты, а ![\delta\in(0,1]](/sites/default/files/tex_cache/6e47be5d0566f026f473f857e33376ae.png) . Значение коэффициента
. Значение коэффициента  зависит от проблемной области и определяется экспериментально. Следует отметить следующие важные аспекты данной модификации РА:
зависит от проблемной области и определяется экспериментально. Следует отметить следующие важные аспекты данной модификации РА:
- Удерживание скорости в некотором диапазоне не ограничивает явно позицию частицы и непосредственно влияет только на размер шага перемещения, который определяется скоростью.
- Максимальное значение скорости ассоциируется с каждой компонентой
 и пропорционально ее области определения. Для упрощения предположим, что по компонентам (измерениям) значения скорости ограничены одной константой
и пропорционально ее области определения. Для упрощения предположим, что по компонентам (измерениям) значения скорости ограничены одной константой  . Тогда, в случае
. Тогда, в случае  в измерении
в измерении  -ой частицы могут значительно отклониться от оптимума в компоненте
-ой частицы могут значительно отклониться от оптимума в компоненте  .
.
Данный подход имеет преимущество в том, что сдерживает резкое увеличение скорости, но пользователь должен следить за этим. Во-первых, ограничение скорости изменяет не только шаг изменения, но и направление движения частицы. Этот эффект показан на рис.11.4 для двумерного случая.
На этом рисунке  обозначает позицию
обозначает позицию  -ой частицы без ограничения скорости, а
-ой частицы без ограничения скорости, а  – ее позицию в результате ограничения скорости по второй компоненте
– ее позицию в результате ограничения скорости по второй компоненте  . Заметим, что при этом направление поиска и величина шага изменились.
. Заметим, что при этом направление поиска и величина шага изменились.
Кроме этого, существует другая проблема в случае равенства всех скоростей максимальных значений по всем компонентам. Если не предусмотрены измерения для предотвращения такой ситуации, то частицы остаются на границе гиперкуба, определяемого как ![[x_i(t)-V_{\max},x_i(t)+V_{\max}]](/sites/default/files/tex_cache/9bdffa07303c7ca210d0f75db4e8124c.png) . Возможно, что частицы могут задержаться в оптимуме, но в общем случае рою трудно искать решение в этой локальной области. Эта проблема может быть решена по-разному - например, путем ввода веса инерции или временным уменьшением значения
. Возможно, что частицы могут задержаться в оптимуме, но в общем случае рою трудно искать решение в этой локальной области. Эта проблема может быть решена по-разному - например, путем ввода веса инерции или временным уменьшением значения  [3].
[3].
Введение веса инерции является также популярной модификацией РА, где контролируется момент частицы путем регулирования вклада предыдущей скорости следующим образом:
 |
( 11.13) |
для глобального РА. Аналогично это делается и для локального РА.
Значение коэффициента  играет большую роль и определяет компромисс между исследованием и локализацией в пространстве поиска. При
играет большую роль и определяет компромисс между исследованием и локализацией в пространстве поиска. При 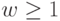 скорость частицы увеличивается (с учетом ранее рассмотренного ограничения) и рой "расходится". Частицам тяжело изменить направление движения для того, чтобы вернуться к перспективной области поиска решения. При
скорость частицы увеличивается (с учетом ранее рассмотренного ограничения) и рой "расходится". Частицам тяжело изменить направление движения для того, чтобы вернуться к перспективной области поиска решения. При  частицы замедляются до тех пор, пока их скорость не станет равной нулю. Таким образом, большие значения
частицы замедляются до тех пор, пока их скорость не станет равной нулю. Таким образом, большие значения  способствуют исследованию пространства поиска, а малые - локализации решения. Однако слишком малые значения
способствуют исследованию пространства поиска, а малые - локализации решения. Однако слишком малые значения  лишают рой способности исследовать пространство поиска. Чем меньше
лишают рой способности исследовать пространство поиска. Чем меньше  , тем больше влияние когнитивной и социальной компоненты. Как и остальные параметры, оптимальное значение
, тем больше влияние когнитивной и социальной компоненты. Как и остальные параметры, оптимальное значение  проблемно-ориентировано (зависит от задачи). В первых реализациях этого подхода использовались постоянные значения
проблемно-ориентировано (зависит от задачи). В первых реализациях этого подхода использовались постоянные значения  . Далее стали использовать динамические
. Далее стали использовать динамические  , где старт производится с большим значением
, где старт производится с большим значением  , которое далее постепенно уменьшается. Выбор значения
, которое далее постепенно уменьшается. Выбор значения  можно совместить с определением значений коэффициентов
можно совместить с определением значений коэффициентов 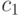 и
и 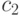 . Например, показано [3], что
. Например, показано [3], что  гарантирует сходимость траектории частицы. Если это условие не выполняется, то возможно расхождение или зацикливание движения частиц.
гарантирует сходимость траектории частицы. Если это условие не выполняется, то возможно расхождение или зацикливание движения частиц.
При динамическом изменении веса инерции обычно применяются следующие методы:
- Случайное регулирование, где различные веса инерции случайно генерируются на каждой итерации. В некоторых случаях используется Гауссово распределение, где
 и
и  достаточно мало, чтобы
достаточно мало, чтобы  не превышало 1. Иногда полагают
не превышало 1. Иногда полагают  без случайного изменения вклада когнитивной и социальной компонент [3].
без случайного изменения вклада когнитивной и социальной компонент [3]. -
Линейное уменьшение веса инерции, например в соответствии с

где
 - максимальное число итераций выполнения алгоритма,
- максимальное число итераций выполнения алгоритма,  – начальный вес,
– начальный вес,  – конечный вес,
– конечный вес,  – текущий вес на итерации
– текущий вес на итерации  . Заметим, что
. Заметим, что  .
. -
Нелинейное уменьшение веса инерции, которое часто позволяет сократить этап исследования пространства поиска и может быть выполнено по-разному:

и другими методами [3].
- Нечеткие (fuzzy) веса инерции на основе нечетких множеств и правил регулирования [3].
Использование коэффициента сжатия (constriction coefficient) является модификацией РА, которая похожа на использование коэффициента инерции. Здесь уравнение изменения скорости частицы выполняется следующим образом:
![v_{ij}=(t+1)=\chi[v_{ij}(t)+\phi_1(y_{ij}(t)-x_{ij}(t))+\phi_2(\hat y_j(t)-x_{ij}(t))],\\\mbox{где}\ \chi=\frac{2k}{|2-\phi-\sqrt{\phi(\phi-4)}|}\ \mbox{c }\phi=\phi_1+\phi_2,\phi_1=c_1r_1\ and\ \phi_2=c_2r_2.](/sites/default/files/tex_cache/2bd6b69a256c093a5cb041e842063238.png)
Этот подход является альтернативой методу ограничения скорости и при ![\phi\ge 4\ and\ k\in[0,1]](/sites/default/files/tex_cache/fdb6951940618059e27ac2fe124d2421.png) гарантирована сходимость роя [3].
гарантирована сходимость роя [3].
Асинхронные версии РА также применяются на практике наряду с синхронными, к которым относится основной РА представленный выше.В синхронных РА изменение персональных лучших позиций и глобальных лучших позиций выполняется синхронно независимо от изменения позиций частиц. В асинхронных РА, напротив, изменение новой лучшей позиции производится после того как каждая частица роя изменила свою позицию.

