Параллельные генетические алгоритмы

4.7.2. Кооперативная коэволюция

Рассмотрим кооперативный ПГА, где значение фитнесс-функции особи зависит от ее способности "сотрудничать" с особями других подпопуляций. Этот подход часто позволяет произвести декомпозицию сложной проблемы на несколько менее сложных задач, каждая из которых решается с помощью ГА. Данный тип ПГА наиболее широко применяется при решении задач многокритериальной оптимизации. Одной из наиболее сложных задач при разработке кооперативной коэволюции является метод определения "премии" (credit assignment) для особи. Основной вопрос - как построить фитнесс-функцию для отдельных особей так, чтобы она учитывала коллективный эффект всех видов.

В некоторых работах [9] предложен общий подход к эволюции сложных решений путем расщепления на подкомпоненты, которые эволюционируют независимо друг от друга. При этом используется отдельная популяция для эволюции каждой подкомпоненты и соответствующий эволюционный алгоритм. Представления (кодирование) каждой компоненты затем комбинируются для образования сложного решения, которое оценивается с помощью глобальной фитнесс-функции. На ее основе определяются обратные кредитные потоки к каждой компоненте, отражающие как хорошо данный компонент сотрудничает с другими. Эта локальная фитнесс-функция затем используется в подпопуляции для эволюции лучшего решения.

Данный подход, в частности, применялся для оптимизации функций многих переменных [10]. При этом для задачи размерности используется подпопуляций – по одной для каждой координаты. Каждая подпопуляция отвечает за оптимизацию по одному из параметров, но в целом ни одна подпопуляция не может образовать полное решение сама по себе. Сотрудничество достигается путем объединения представлений решений для каждой подпопуляции. Эффективность такого сотрудничества оценивается следующим образом. При рассмотрении -ой подпопуляции 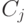каждая особь "сотрудничает" с лучшей особью их каждой подпопуляции путем объединения этих лучших компонент с в полное решение. В этом случае определение "премии" особи сводится просто к вычислению значения глобальной фитнесс-функции полного решения.

Экспериментальные исследования показали [10], что этот подход не дает хорошие результаты в том случае, когда параметры задачи сильно взаимосвязаны вследствие использования жадной эвристики в определении премии особи. Для уменьшения этого эффекта предложено использовать два дополнительных вектора. Первый вектор строится на основе лучших особей каждой подпопуляции, как описано ранее. Второй вектор выбирает случайные особи из других подпопуляций и "склеивает" их с . Лучшее значение фитнесс-функции этих двух векторов затем используется в качестве премии (кредита) для . Кроме решения задач многомерной оптимизации авторы использовали этот подход при обучении каскадных нейронных сетей[11] и обучения роботов[12].

4.8. Инструментарий распараллеливания

Как отмечалось выше, для реализации ПГА могут быть использованы компьютерные системы с различными архитектурами: SISD, SIMD, MIMD и т.д. Вместо описания многочисленных специальных архитектур и программных конструкций, которые используются при реализации ПГА, далее мы кратко рассмотрим те параллельные и распределенные модели, которые не зависят от конкретных структур. Почти все ПГА реализуются на основе модели каналов для передачи сообщений в коммуникациях, поскольку они позволяют описывать многопроцессорные системы с распределенной памятью, которые являются наиболее удобным и распространенным средством реализации ПГА. В модели передачи сообщений процессы в одном или физически различных процессорах сообщаются между собой путем передачи друг другу сообщений через среду коммуникации, которая представлена стандартом или специальной схемой соединения. Основными элементами здесь являются процедуры отправления и приема сообщений. В простейшей форме, отправление определяет локальный буфер передаваемых данных. Процедура приема обычно определяет процесс отправления и локальный буфер, в котором сохраняются входящие данные. В качестве инструментария чаще всего используются следующие средства: сокет (sockets), параллельная виртуальная машина (parallel virtual machine -PVM), интерфейс передачи сообщений (message passing interface - MPI), Ява (Java), архитектура общего назначения запрос-посредник (common object request broker architecture) - CORBA и Globus, которые обеспечивают большие функциональные возможности, чем простой сервис передачи сообщений.

Контрольные вопросы

1. Какие свойства ГА способствуют его распараллеливанию?
2. Опишите модель "рабочий - хозяин".
3. Каковы функции процессора – хозяина?
4. Что делает процессор – рабочий?
5. Какой выигрыш дает модель "рабочий - хозяин"?
6. Чем отличается модель "рабочий - хозяин" от "модели островов"?
7. Какие факторы влияют на миграцию в "модели островов"?
8. Какие вы знаете виды распределенных ГА?
9. Опишите клеточные ГА.
10. Что такое виртуальные острова?
11. Что такое коэволюционные ГА?
12. Приведите различные варианты реализации параллельных ГА.
13. Какой инструментарий можно использовать при реализации ГА?
14. Опишите возможный вариант иерархического ГА.