Межотраслевой баланс

Цель лекции. Научить строить модель МОБ. Вводить данные в виде матриц. Производить действия с матрицами: транспонирование, умножение, находить суммы элементов. Рассчитывать матрицы межотраслевого баланса.

3.1. Моделирование межотраслевого баланса

Межотраслевой баланс - инструмент анализа и прогнозирования структурных взаимосвязей в экономике. Метод построения межотраслевого баланса состоит в двойственном рассмотрении различных отраслей и секторов экономики: с одной стороны, как потребляющих продукцию, с другой - как выпускающих те или иные виды товаров и услуг для собственного потребления и нужд других отраслей экономики. Метод "затраты-выпуск",.разработанный Леонтьевым, позволяет анализировать межотраслевые связи первичных затрат выпуска продукции в отдельных отраслях и конечного спроса на них и предоставляет информацию, которую практически невозможно получить, применяя другие методы и модели макроэкономического анализа [15,16,17].

Основу межотраслевого баланса составляет совокупность всех отраслей материального производства. Предположим, что экономическую систему имеет n отраслей, производящих определенные товары и услуги. При производстве товаров и услуг в каждой отрасли расходуются определенные ресурсы, которые производятся как в других отраслях, так и в данной отрасли. Каждая отрасль экономики выступает в системе межотраслевых связей одновременно производителем и потребителем.

Цель балансового анализа - определить, сколько продукции должна произвести каждая отрасль для того, чтобы удовлетворить все потребности экономической системы в его продукции [15]. Процесс производства рассматривается за некоторый период времени, например, за год. Часть продукции идет на производственное потребление данной отраслью и другими отраслями, а другая часть предназначена для потребления вне сферы материального производства. В зависимости от того, в каких единицах измерения записываются соотношения баланса, различают натуральный или стоимостной межотраслевые балансы.

Все отрасли производственной сферы экономики представляются в виде таблицы (- строки, -столбцы). Каждая отрасль будет дважды фигурировать в балансе: как производящая и как потребляющая. Обозначим:

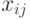– стоимость продукции -й отрасли, затраченной -й отраслью на производство в течение года;

– стоимость валового продукта, потребленного -й отраслью в течение года. 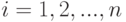; Строка . – сумма всех поставок -й отрасли для производства другим отраслям и конечного продукта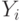

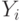— объем продукции –й отрасли, предназначенный к потреблению в непроизводственной сфере (объём конечного потребления). В этот объём входят личное потребление граждан, создаваемые хозяйственные запасы, экспорт, инвестиции, обеспечение общественных потребностей. Структура конечного продукта ,где 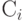- конечное потребление , 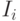- инвестиции, 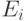- экспорт и – импорт. Сальдо во внешней торговле .

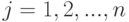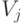– стоимость валового продукта, произведенного -й отраслью в течение года, . ;. Столбец – сумма затрат -й отрасли на производство продукции других отраслей и добавленной стоимости ,произведенных -й отраслью в течение года.

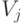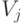
- добавленная стоимость, –й отрасли. Структура добавленной стоимости продукта ,, где 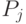оплата труда, 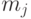– чистый доход (прибыль), 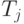,- налоги.

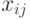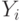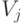Элементы образуют матрицу межотраслевых поставок. Уравнения баланса выражают тот факт, что валовой выпуск расходуется на производственное потребление, равное и непроизводственное потребление, равное . - сумма затрат на производство продукции других отраслей и добавленной стоимости ,произведенных -й отраслью в течение года.

( 3.1)

( 3.2)

Делается допущение, что материальные издержки пропорциональны объему производимой продукции.

Для любой пары отраслей можно записать , где -постоянный коэффициент. Таким образом, имеем

( 3.3)

Величины - коэффициенты прямых затрат - количество продукции -ой отрасли, которое расходуется при производстве одной единицы продукции -ой отрасли. Эти величины остаются постоянными в течение ряда лет, поскольку технологии производства также остаются постоянными или мало меняются за указанный промежуток времени.

Соотношения баланса, записанные через коэффициенты прямых затрат, имеют вид::

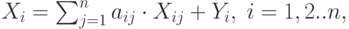( 3.4)

Уравнения описывают технологию производства и структуру экономических связей и означают, что в сектор конечного спроса от каждого производственного сектора поступает та часть произведенной продукции, которая остается после того, как обеспечены потребности производящих секторов.

Записывая уравнения в матричной форме получаем

( 3.5)

где - вектор валовых выпусков; - вектор конечного продукта; - матрица прямых затрат

Свойства коэффициентов прямых материальных затрат

1. 1. Неотрицательность, т.е. . Это утверждение следует из неотрицательности величин x_{ij} и положительности валовых выпусков .
2. 2. Поставки самому себе по определению меньше валового выпуска . Следовательно: .
3. 3. Сумма элементов матрицы по любому из столбцов меньше единицы, т.е.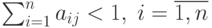

Обозначая - единичную матрицу, уравнение (3.5) можно записать в виде

( 3.6)

Если существует обратная матрица , то из (3.6) следует равенство

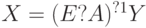( 3.7)

Однако, для того, чтобы решение имело экономический смысл, необходимо, чтобы при любом задании вектора конечной продукции, т. е. при любых положительных Y>0. С математической точки зрения это означает , что матрица должна быть продуктивна.

Матрица A называется продуктивной, если для любого вектора существует решение уравнения (3.7). При этом модель Леонтьева называется продуктивной.

Справедливы следующие критерии продуктивности.

• Матрица продуктивна тогда и только тогда, когда матрица существует и неотрицательна.
• Если матрица продуктивна, то матрица представима суммой сходящегося степенного матричного ряда:

Обратную матрицу обозначим через . Матрица 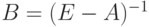называется матрицей полных затрат. Тогда уравнение (3.7) имеет вид:

( 3.8)

Элементы матрицы - - 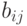коэффициенты полных затрат, 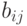показывает, каков должен быть валовой выпуск -й отрасли для того, чтобы обеспечить выпуск единицы конечного продукта -отрасли.